水平軸風力機葉片氣彈建模與響應分析

陸 洋， 周桂林

（南京航空航天大學 旋翼動力學國防科技重點實驗室，江蘇 南京210016）

0 引 言

大型水平軸風力機系統是強非線性流－剛柔耦合的周期時變多體系統，結構和運動關系非常復雜，對風力機葉片進行動力學建模時必須考慮葉片的幾何非線性以及非定常氣動載荷等因素，理論推導和數值計算都比較困難。另一方面，隨著風力機額定功率不斷增加，葉片尺寸越來越大，細長葉片在交變載荷下的揮舞變形更大。為防止葉尖與塔架碰撞，出現了預彎葉片設計概念，增加了風力機葉片氣彈建模的難度。

風力機葉片氣彈建模包括葉片結構動力學建模和空氣動力學建模。文獻［1］采用模態分析法進行葉片結構動力學建模，采用Greenberg's二維準定常氣動力模型計算氣動力，研究了風力機氣彈穩定性；文獻［2］采用5節點18自由度梁單元對葉片進行有限元離散，采用二維準定常氣動模型，利用擬線性法計算了水平軸風機工作狀態下的氣動彈性響應；文獻［3］以Marc有限元軟件為基礎平臺，采用動量葉素理論二維氣動力模型，計算葉片的氣彈響應；文獻［4］采用二節點梁單元對葉片進行有限元離散，采用Leishman－Beddoes非定常模型計算氣動力，分析了葉片的動態響應。

可見，為了保證葉片響應的計算精度，有限元方法已逐漸替代模態法成為風力機葉片結構動力分析的主流方法，氣動力建模則仍以動量葉素理論和二維準定常氣動力模型為主。

然而，現有的葉片氣彈建模方法仍存在以下局限性：1）基于有限元方法的風力機動力學方程通常建立在非慣性系下，即處理動能部分時將其分為旋轉坐標系的動能和牽連運動引起的動能兩部分，破壞了推導和編程的一致性；2）建模時，沒有考慮葉片預彎對葉片氣動彈性動力響應的影響；3）氣動力模型多采用二維準定常空氣動力計算模型，沒有考慮葉片動態入流以及動態失速影響。這些局限性，使得傳統建模方法的計算精度和適用性受到了制約。

針對前述葉片建模方法的局限性，本文開展了如下工作：1）引入了Hartenberg－Denavit增廣轉換矩陣［5］，通過遞歸計算的方式得到慣性坐標系下的位置矢量，從而在慣性系下建立了風力機葉片動力學方程，將動能部分合為一體，避免了傳統建模中的繁瑣；2）引入上反坐標系方法描述風力機葉片的預彎變形，考慮了預彎變形影響；3）入流模型采用Suzuki提出的針對風機葉片的廣義動態尾跡入流模型（GDW）［6］，并采用Pierce修正的風機Leishman－Beddoes模型［7］計算翼型非定常氣動力，綜合考慮了葉片動態入流以及動態失速影響。利用Newmark數值積分方法求解葉片動力學方程獲得穩態周期解。最后，分別以美國可再生能源實驗室（NREL）Phase VI非定常空氣動力學實驗風力機［8－9］及其公開的1.5MW風力機葉片［10］為算例計算了有／無預彎葉片的氣彈響應，驗證了本文所建模型的正確性和有效性。

1 系統坐標系

1.1 增廣轉換矩陣

為描述風力機葉片復雜的結構形式及運動特點，引入多個坐標系，表1給出了建立風力機系統的坐標系定義和描述。圖1為風力機系統坐標系示意圖。對于開環拓撲結構，如果要描述梁剖面上的任意一點P，在變形后的坐標系下，可以將位置矢量表示為：

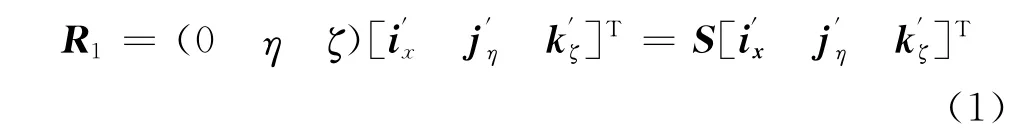
將位置坐標行向量S增廣為：

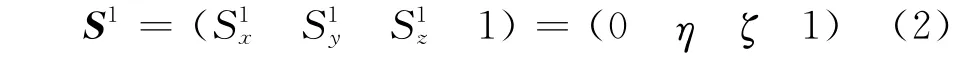
在未變形坐標下，增廣后P點的位置增廣向量及增廣轉換矩陣為：

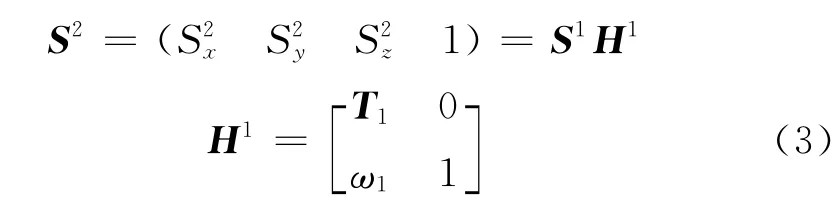
根據式（3）類推，在n個坐標系中第i個坐標系下，P點的位置增廣向量及增廣轉換矩陣為：

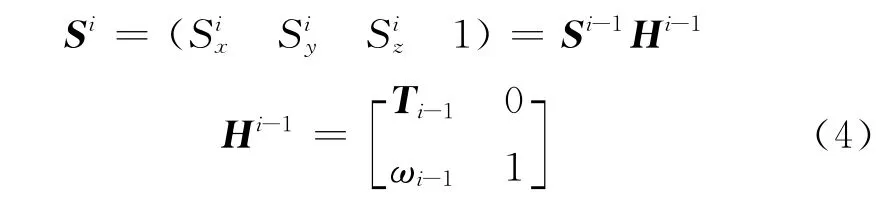
依次類推，在慣性坐標系下，葉片上任意點P的位置增廣向量表示為：

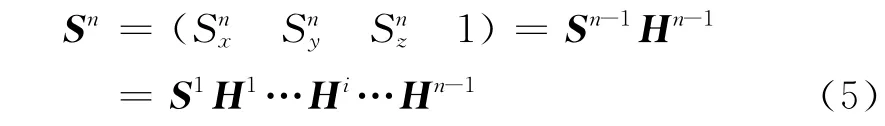
由上面的遞歸表達式（4）可以看出，只要確定了各坐標系原點的位置和轉換關系，就可以通過遞歸計算的方式得到慣性坐標系下的位置矢量，從而簡化了剛柔耦合計算，使推導和編程也得到簡化，提高了算法對風力機結構和運動形式的適用性。

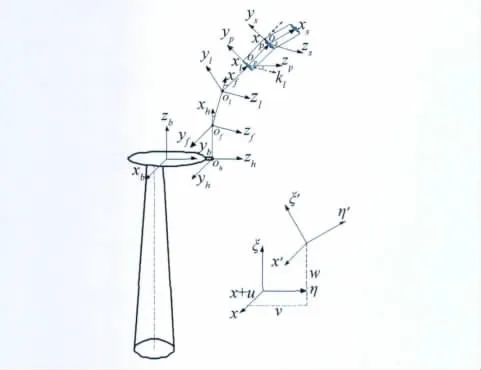
圖1 風力機系統坐標系示意圖Fig.1 Schematic of coordinate system of wind turbine

表1 風力機坐標系統Table 1 Coordinate system of wind turbine

1.2 上反坐標系

葉片設計時預先向偏離塔架方向彎曲，可以增大葉尖與塔架之間的凈空間隙，減少二者發生碰撞的可能性。大型風力機葉片長度通常超過30m，葉片一般從1／3長度位置處開始預彎。對于長度為35m左右的1.5MW風機葉片，預彎高度一般取值為600～750mm。由于預彎值遠小于葉片長度，為了描述預彎部分葉片的位置矢量，本文提出一種簡化處理辦法，如圖2所示，用直線葉片BC′來替代連續預彎葉片部分BB′C′，直線葉片BC′的上反角度為ζ0。因此，為了描述整個葉片的位置矢量，需要將葉片劃分為AB和BC′兩段進行處理，在BC′段引入上反坐標系Rs：osxsyszs。

圖2 預彎葉片示意圖Fig.2 Sketch of pre－curved rotor blade

上反坐標系與變距坐標系之間的轉換關系Ts為：

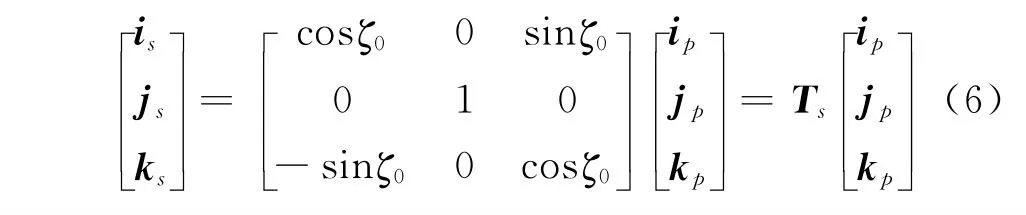
對于預彎量較大的葉片，可以采用類似方法，引入多個上反坐標系。引入的上反坐標系越多，則預彎變形情況描述越精確，綜合考慮計算效率，可選擇適當數量的上反坐標系進行計算。

2 葉片動力學建模

2.1 葉片單元彈性勢能貢獻項

采用中等變形梁理論得到Green應變表達式［11］，帶入單元彈性勢能表達式并對其求變分，得到彈性廣義力及彈性勢能貢獻項：

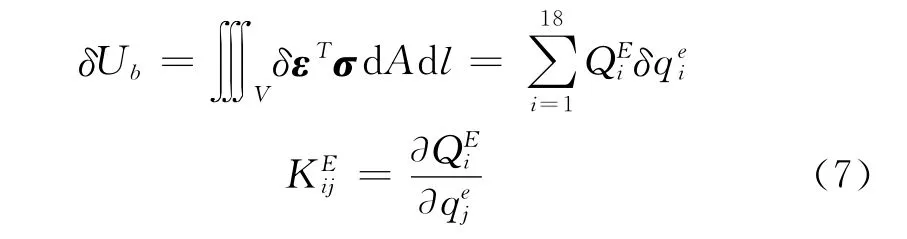
2.2 葉片單元動能貢獻項

單片葉片上的動能變分［12］可以表示為：

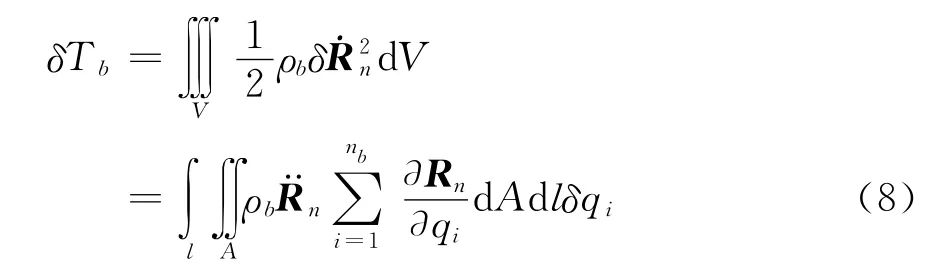
經推導得動能產生的第i個廣義力為：

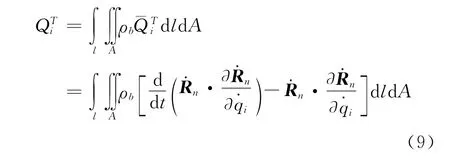
動能所產生的切線質量、阻尼和剛度陣為：

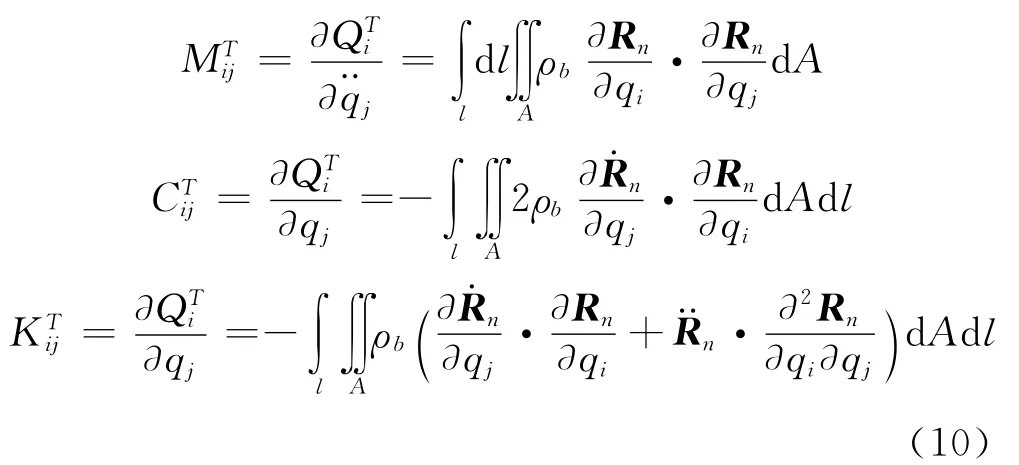
為了計算質量、阻尼和剛度陣，還需求出增廣位置矢量的相關導數和偏導數，利用遞推算法后，可使推導通用性大大提高，避免了傳統建模中的繁瑣。

2.3 重力功貢獻項

在計算風力機風輪葉片氣彈響應時，必須考慮葉片的重力影響，葉片重力引起的外力功和重力廣義力分別為：

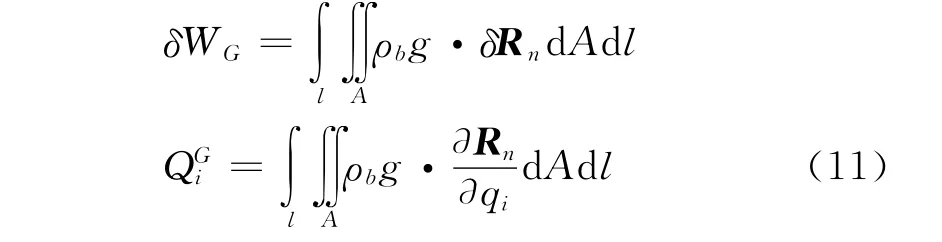
2.4 氣動力貢獻項

誘導速度計算采用Suzuki廣義動態尾跡模型［6］。用任意諧波次數和任意階次徑向型函數的級數形式來描述風輪平面垂向誘導速度：

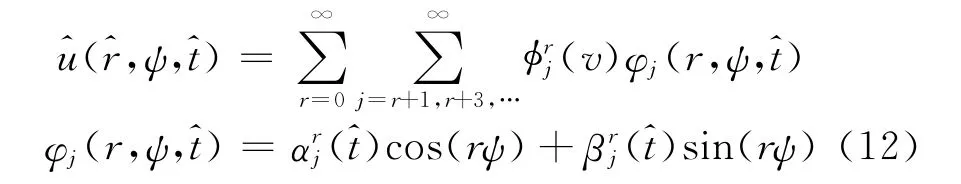
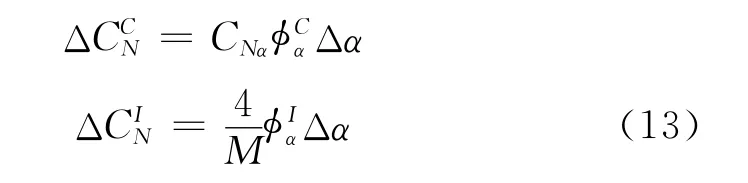
其中，Δ為環量項，Δ為非環量項。利用Kirchhoff理論處理翼型后緣分離的非線性問題，翼型法向力系數和弦向力系數與分離點的關系為：

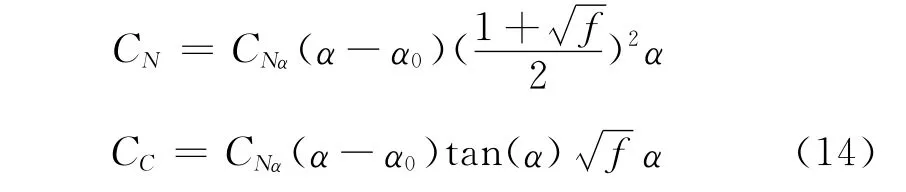
式中、ψ分別是無量綱半徑、方位角和無量綱時間。是徑向函數，是基于時間的狀態量。

翼型剖面非定常氣動力計算采用Pierce修正后應用于風力機計算的Leishman－Beddoes模型［7］。該模型通過階躍響應的疊加模擬附著流條件下的非定常效應：

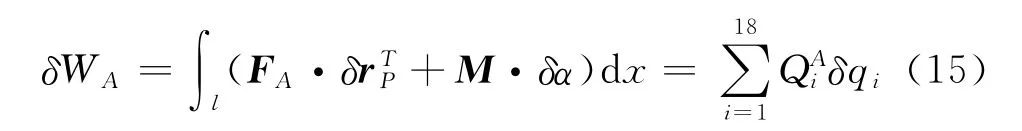
2.5 葉片動力學方程

應用Hamilton原理建立系統運動方程：

其中，CN是法向力系數，CC是弦向力系數，f是分離點位置。根據動態失速的特性，模擬動態失速渦沿翼型上表面的移動及因而引起的壓力中心的移動，從而計算動態失速渦誘導產生的升力和俯仰力矩［9］。空氣動力FA及力矩MA所做虛功的變分可以表示為：

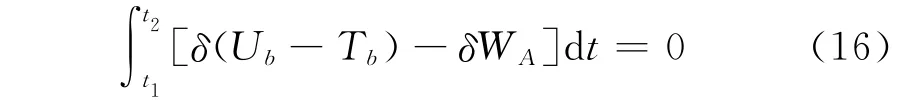
對式（16）進行變分運算和有限元離散，組集動能、應變能及空氣動力等產生的虛功，得到基于廣義力形式的葉片非線性動力學隱式微分方程：

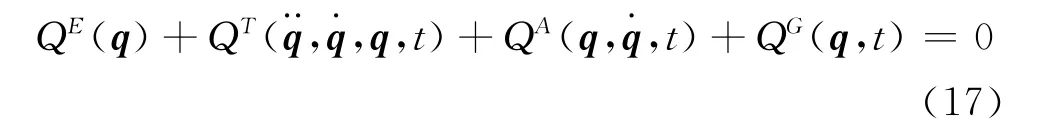
式中右上標T、E、A、G分別表示動能、應變能、氣動力及重力引起的廣義力，q、、為廣義位移、速度、加速度向量。

由于建模過程中考慮了葉片整體的剛性運動與葉片自身彈性運動間的剛柔耦合特點及非定常和動態失速等非線性因素，最終采用適應性較強的Newmark數值積分方法進行運動方程求解。

3 算例驗證

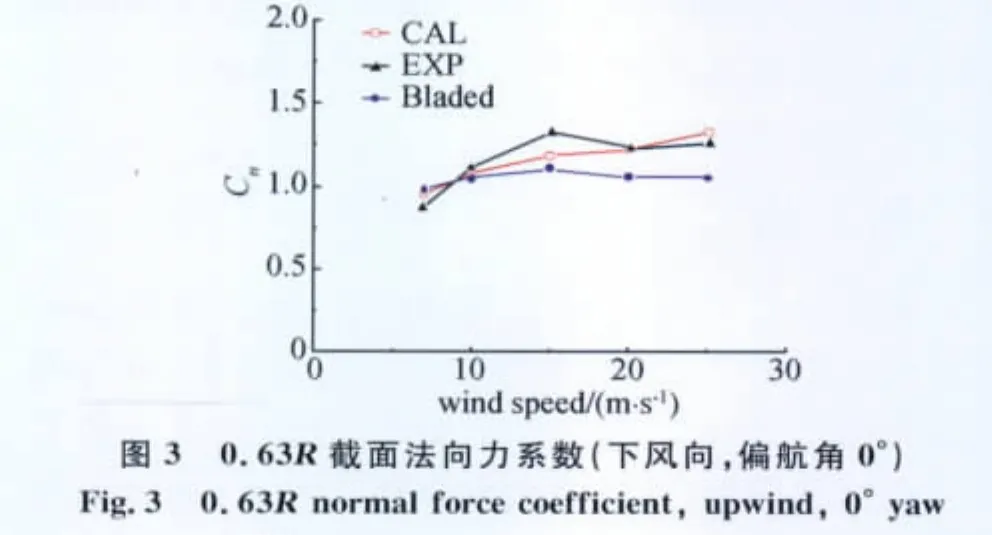
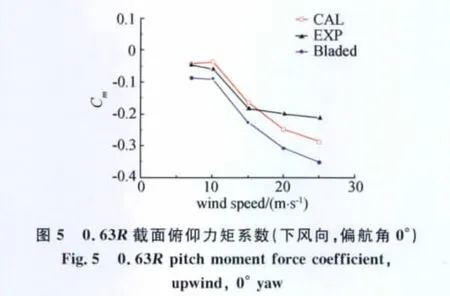
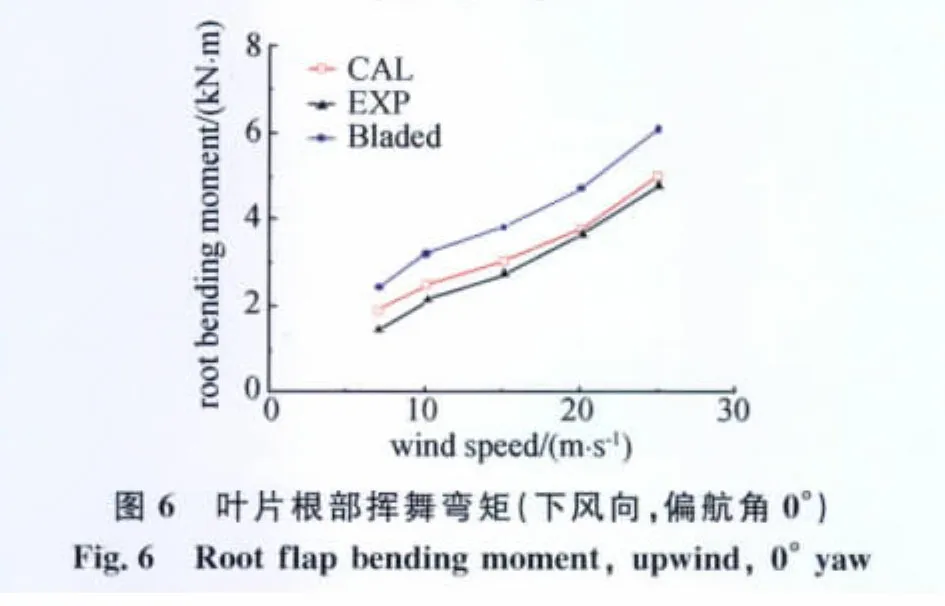
算例1：對NREL Phase VI非定常空氣動力學實驗中葉片長度為10.058m的小型水平軸風力機進行計算并與Bladed軟件以及實驗結果比較。本文分別計算了來流速度分別為 7m／s、10m／s、15m／s、20m／s、25m／s，偏航角為0°時，下風向風機徑向位置為63%截面的法向力系數Cn，切向力系數Ct，俯仰力矩系數Cm以及葉片根部的揮舞力矩。圖3～圖6為本文計算結果與實驗數據及Bladed計算結果的對比曲線。

從圖3～圖5可以看出，相比較Bladed計算結果，本文計算得到的截面氣動力系數與實驗結果吻合程度更佳，表明了本文葉片氣彈建模中空氣動力學建模方法的正確性和精確性。圖6中計算結果與實驗值的葉片根部揮舞彎矩吻合程度較高，而葉片根部揮舞力矩主要由氣動力貢獻，再次證明了本文氣動力模型的正確性。

算例2：以NREL 1.5MW下風向風機葉片為算例進行氣彈響應計算。該風機基本參數如下：風輪仰角η＝0°，風輪錐角χ＝0°，葉片長度33.25m，輪轂半徑1.75m，來流速度10m／s，風輪轉速20rpm。葉片無預彎，剖面特性具體參數見文獻［8］。為了分析葉片預彎對葉片氣彈響應的影響，假設該葉片在1／3位置處開始連續預彎，至葉尖處預彎高度為3.5m，即上反角10°，計算該預彎葉片的氣彈響應。將上述計算結果與NREL公開文獻的計算結果一并進行對比分析，以驗證本文算法的正確性。圖7～圖12給出了葉片旋轉系下單片葉片作用于輪轂三個方向的載荷及力矩沿方位角變化對比曲線。

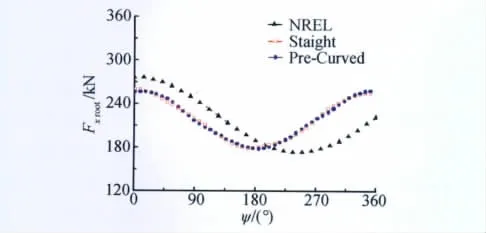
圖7 葉片根部徑向載荷Fig.7 Blade axial force at blade root

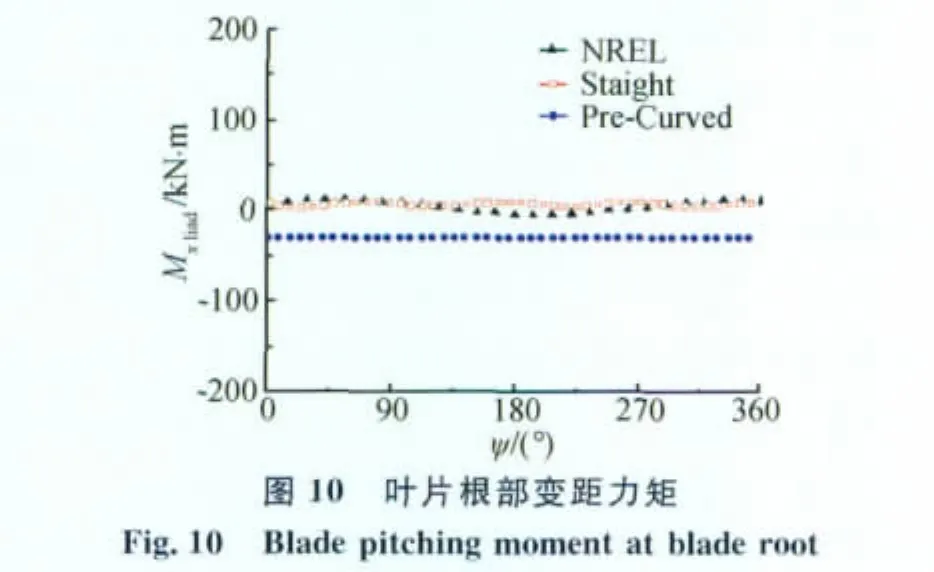
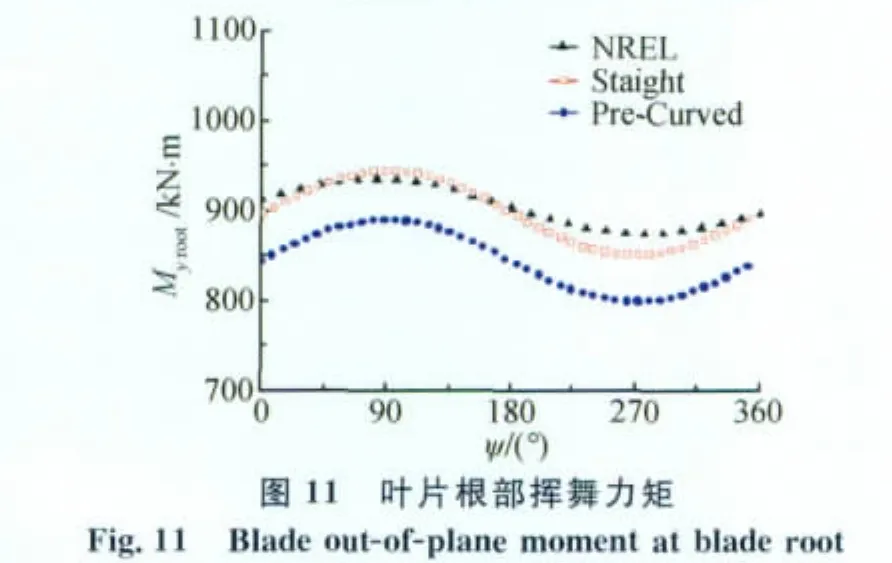
對比無預彎情況下葉片在旋轉系下的載荷和力矩，本文計算結果與NREL公開文獻的計算結果的變化趨勢以及幅值符合較好，其中葉片徑向載荷的相位存在約50°的差異。由于葉片徑向載荷主要由風輪旋轉產生的離心力和周期變化的重力載荷分量構成，考慮重力載荷在葉片徑向周期變化，可知本文計算結果更加合理。通過無預彎情況的算例對比，驗證了本文建模算法的正確性。

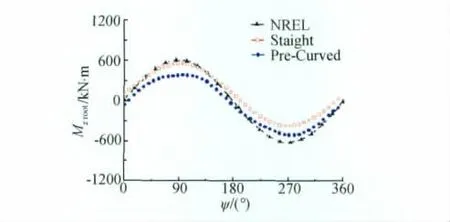
圖12 葉片根部擺振力矩Fig12 Blade in－plane moment at blade root

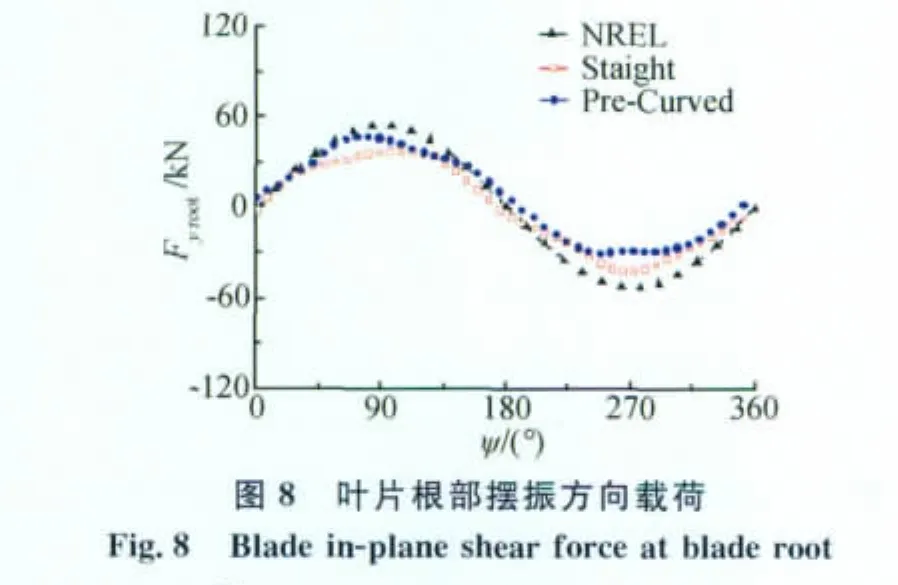
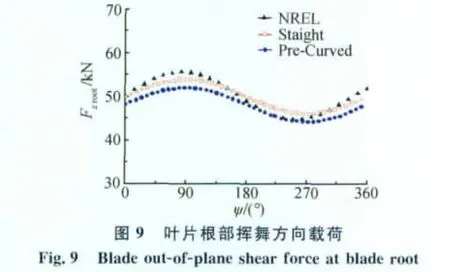
對比有／無預彎兩種情況下基于本文模型計算所得的葉片載荷和力矩，可以看出對于下風向風機預彎對葉片的徑向載荷以及擺振方向的載荷影響不大（圖7、圖8），這是因為葉片擺振方向的載荷主要是周期變化的重力載荷，預彎對重力載荷基本沒有影響。同理，由于葉片擺振力矩主要為擺振載荷貢獻，預彎對擺振力矩影響也很小（圖12）。由圖9和圖11可知，預彎使得葉片揮舞方向載荷、力矩的穩態值變小。揮舞方向載荷的穩態值主要為氣動力，表明預彎降低了葉片氣動力載荷。由圖10葉片變距力矩對比曲線可以看出，預彎使得葉片變距力矩的絕對值增大。影響葉片變距力矩的因素很多，其中最重要的是由葉片自身質量引起的離心力作用而產生的慣性力矩和變距結構各種摩擦副產生的摩擦阻力距。下風向風機葉片由于預彎增加了葉片離心力作用產生的慣性力矩，從而使葉片變距力矩顯著增加。通過上述分析可知，本文采用上反坐標系處理葉片預彎變形的方法所得到的預彎影響與理論分析相符，表明該處理方法是合理的。

4 結 論

本文基于Hamilton原理，建立了水平軸風力機葉片的氣彈模型。通過數學建模和算例分析，可以得到以下結論：1）引入增廣轉換矩陣，在慣性系下建立葉片動力學方程，可以簡化剛柔耦合計算，避免傳統建模中的繁瑣；2）氣動力建模時，采用Suzuki廣義動態尾跡方法計算誘導速度，采用Pierce修正的風機Leishman－Beddoes模型計算翼型氣動力，可提高了氣動力計算精度，比Bladed計算結果更符合實驗值；3）本文所建模型預測的無預彎葉片的載荷與NREL計算結果符合較好；4）采用上反坐標系處理葉片預彎變形，計算所得的預彎影響與理論分析相符，驗證了本文所建立的可考慮葉片預彎的氣彈動力學模型的合理性。

［1］李本立，安玉華.風力機氣動彈性穩定性研究［J］.太陽能學報，1996，17（4）：314－320.

［2］王介龍，陳彥，薛克宗.風力發電機耦合轉子／機艙／塔架的氣彈響應［J］.清華大學學報（自然科學版），2002，42（2）：211－215.

［3］傅程，王延榮.風力發電機葉片氣動彈性響應分析［J］.機械設計與研究，2009，25（1）：68－71.

［4］LIU X，ZHANG X M.Dynamic response analysis of the rotating blade of horizontal axis wind turbine［J］.WindEngineering，2010，34（5）：543－559.

［5］GERADIN M，CARDONA A.Kinematics and dynamics of rigid and flexible mechanisms using finite elements and quaternion algebra［J］.ComputationalMechanics，1989，18（4）：651－659.

［6］SUZUKI.Application of dynamic inflow theory to wind turbine rotors［D］.［Doctoral Dissertation］.Salt Lake City：Department of Mechanical Engineering，University of Utah，2000.

［7］KIRK GEE PIERCE.Wind turbine load prediction using the Beddoes－Leishman model for unsteady aerodynamics and dynamic stall［D］.［Doctoral Dissertation］.Salt Lake City：Department of Mechanical Engineering，University of Utah，1996.

［8］HAND M M，SIMMS D A.Unsteady aerodynamics experiment phase VI：wind tunnel test configurations and available data campaigns［R］.NREL／TP－500－29955，2001.

［9］HAND M M，SIMMS D A.NREL unsteady aerodynamics experiment in the NASA－Ames Wind Tunnel：A comparison of predictions to measurements［R］.NREL／TP－500－29494，2001.

［10］JASON M.FAST user's guide［R］.Technical Report NREL／EL－500－38230，2005.

［11］王浩文，高正，鄭兆昌.前飛狀態下直升機旋翼系統氣彈響應及穩定性分析［J］.振動工程學報，1999，12（4）：521－528.

［12］王益鋒.直升機旋翼槳葉動力學建模與彈性碰撞動響應分析［D］.［博士學位論文］.南京：南京航空航天大學，2009.