周期脈沖序列作用下單模激光線性模型的隨機共振
汪志云, 陳培杰, 張良英 (湖北文理學院物理與電子信息工程學院,湖北 襄陽 441053)
周期脈沖序列作用下單模激光線性模型的隨機共振
汪志云, 陳培杰, 張良英 (湖北文理學院物理與電子信息工程學院,湖北 襄陽 441053)
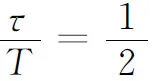
激光光學;周期脈沖序列;功率譜;信噪比;隨機共振
在現代激光通信中,激光常被用來作為信號的傳送器,由于激光系統中存在量子噪聲和抽運噪聲,激光器的工作總是伴隨著漲落的出現。如何減小激光輸出光強的漲落,消除和抑制噪聲對傳輸信號的影響,增加激光的輸出穩定性,一直是提高激光器和激光通信質量的重要研究課題并取得了較大進展,為優化激光通信系統提供了理論依據[1-2]。
對于單模激光系統,曹力等[3-5]首次將信號與考慮關聯的泵噪聲和量子噪聲相乘的形式引入單模激光系統,運用線性近似的方法,在激光系統中發現了信噪比隨關聯強度的變化出現單峰的隨機共振。張良英等[6-14]運用該方法,研究了不同噪聲驅動下的單模激光增益線性模型初態和瞬態的隨機共振現象,以及調幅波和調頻波在各種關聯噪聲驅動下單模激光系統的隨機共振。在上述研究工作中,輸入的信號都采用周期余弦信號,而對于周期脈沖序列作用下的單模激光系統隨機共振的研究很少。為此,筆者構建周期脈沖序列信號和白噪聲共同驅動下單模線性激光模型,通過傅里葉級數展開的方法處理脈沖信號,計算了輸出信號的功率譜和信噪比,討論了系統中的隨機共振現象。
1 周期脈沖序列和白噪聲驅動下的單模激光信噪比
單模激光線性增益模型在輸入周期矩形脈沖序列后的光強方程為:
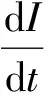
(1)
式中,I為激光光強;β和Γ分別為自飽和系數和增益系數;K為損失系數;ξ(t)和η(t)分別為泵噪聲和量子噪聲;D為量子噪聲強度;f(t)為周期矩形脈沖序列,在1個周期內其表達式為:
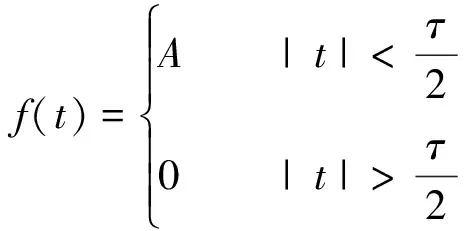
(2)
泵噪聲和量子噪聲的統計性質為:
〈ξ(t)〉=〈η(t)〉=0 〈ξ(t)ξ(t′)〉=Qδ(t-t′) 〈η(t)η(t′)〉=Dδ(t-t′)
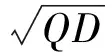
(3)
式中,λ為噪聲關聯系數;Q為泵噪聲的強度。
將信號f(t)展開為三角形式傅里葉級數:
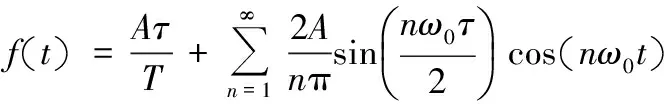
(4)
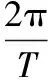
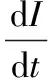
(5)
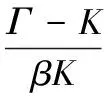
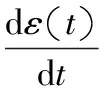
(6)
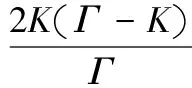
由式(6)可解得:
(7)
根據平均光強相關函數的定義:
由式(3)和式(7)可以求得〈ε(t)〉、〈ε(t+t′)〉和〈ε(t)ε(t+t′)〉,代入式(8)可以得到平均光強相關函數(γ≠τ-1):
(9)
將式(9) 式進行坐標平移,去掉常數項后進行傅里葉變換,得到光強功率譜為:
S(ω)=S1(ω)+S2(ω)
(10)
式中,S1(ω)為輸出信號功率譜;S2(ω)為輸出噪聲功率譜:
S1(ω)中包含2個δ函數,若只取正ω的譜,其表達為:
(11)
S2(ω)在各個頻率處的表達式為:
(12)
由式(11)可得到輸出信號的總功率為:
(13)
將輸出信號總功率與輸出信號中各個頻率處單位噪聲功率之和的比值定義為信噪比(SNR),即:
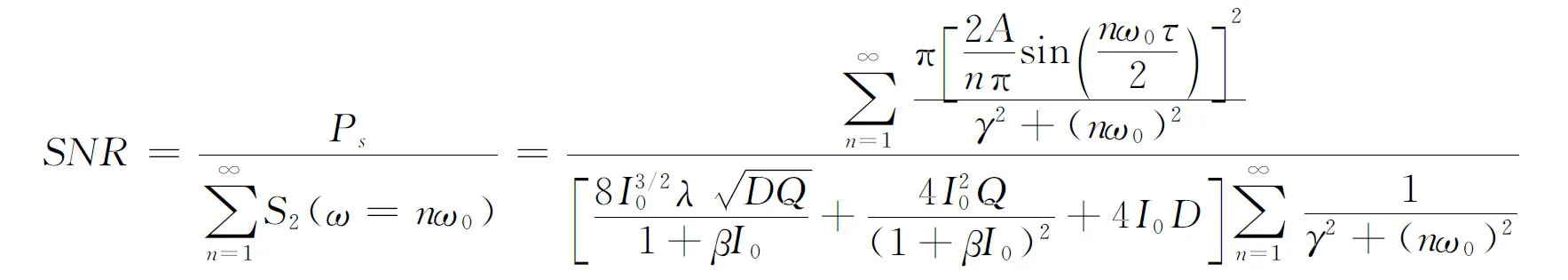
(14)
2 輸出信號光強的隨機共振
2.1信噪比隨泵噪聲強度Q和量子噪聲強度D的變化
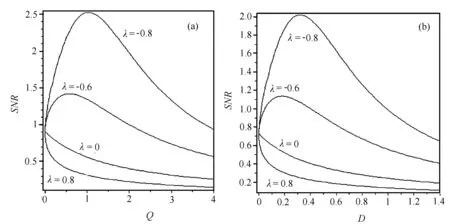
圖1 信噪比SNR在不同的噪聲關聯系數λ下隨噪聲強度Q和D的變化
根據式(14)在噪聲關聯系數λ取不同值時,信噪比(SNR)隨泵噪聲強度Q和量子噪聲強度D的變化曲線如圖1所示。從圖1可以看出,不同λ值的SNR-Q和SNR-D曲線的起點相同;當λ≥0時,信噪比隨噪聲強度單調減小,沒有出現隨機共振現象;在λlt;0時,信噪比隨噪聲強度的變化均出現了隨機共振現象,峰值隨|λ|的增大而增大,其位置向右移動。上述現象是傳統的隨機共振現象,與周期余弦信號作用下的單模激光隨機共振現象是相同的。
2.2周期脈沖信號對光強隨機共振的影響
圖2所示的是脈沖振幅、周期和脈寬不同時信噪比SNR隨泵噪聲強度Q的變化曲線。當輸入信號振幅增大時,SNR-Q曲線整體上移,其共振峰變得更加尖銳,峰值的位置并不發生改變(見圖2(a))。當脈沖寬度τ=0.6、脈沖周期T取不同值時,SNR-Q共振曲線的起點不相同,峰值的位置不發生改變;當脈沖周期Tlt;1.2(2τ)時,隨著T的增大,SNR-Q曲線的共振峰增高,且更加尖銳;而當Tgt;1.2(2τ)時,共振峰卻隨著T的增大而降低(見圖2(b))。當脈沖周期取定值(T=1),脈寬τ取不同值時,SNR-Q曲線的峰值大小不同,其位置相同;在τlt;0.5(T/2)時,曲線的共振峰隨τ的增大而升高;當τgt;0.5(T/2)時,SNR-Q曲線的共振峰隨τ的增大而降低(見圖2(c))。上述現象說明脈沖寬度和周期對SNR-Q共振曲線的影響基本相同。
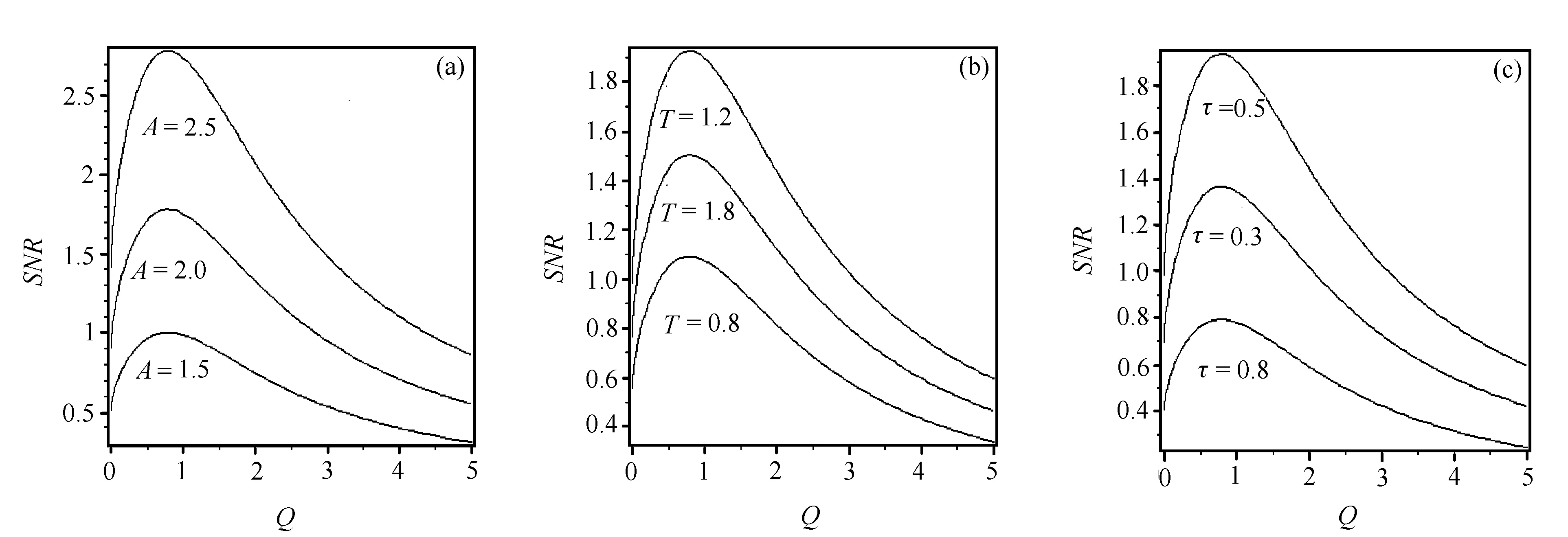
圖2 脈沖振幅、周期和脈寬不同時信噪比SNR 隨泵噪聲強度Q的變化
2.3信噪比隨脈沖周期T和脈沖寬度τ的變化
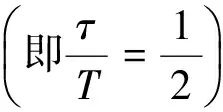
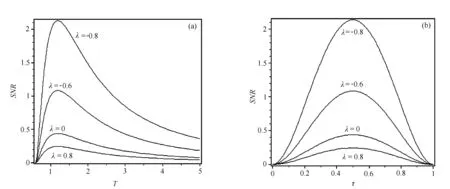
圖3 信噪比SNR在不同的噪聲關聯系數λ值下隨脈沖信號周期T和寬度τ的變化
[1]祝恒江,吳錫田. 隨機共振研究進展[J].大學物理,1997,16(7):28-31.
[2]劉立,吳大進.隨機共振研究新進展[J].大學物理,2009,28(9):46-49.
[3]CAO Li, WU Dajin. Stochastic Resonance in a Linear System with Single-modelated[J].Earophys Leet, 2003,61(5):593-598.
[4]CAO Li, WU Dajin. Stochastic Resonance for Systems Driven by Correlated Noise[J].Phys Lett A, 1994,185(1):59-64.
[5]CAO Li, WU Dajin. Effects of Saturation in the Transient Process of a Dye Laser[J].Phys Rev A, 1992,45(9):6848-6856.
[6]張良英,曹力,吳大進.指數形式關聯噪聲驅動下單模激光線性模型的隨機共振[J].中國激光,2004,31(1):53-56.
[7]張良英,曹力,吳大進.具有色關聯的色噪聲驅動下單模激光線性模型的隨機共振[J].物理學報,2003,52(5) :1174-1178.
[8]張良英,曹力.信號調制噪聲的單模激光隨機共振[J].華中科技大學學報,2005,33(8):119-120.
[9]ZHANG Lingying,CAO Li,WU Dajin. Stochastic Resonance in a Single-mode Laser Driven by Quadratic Colored Pump Noise:Effects of Biased Amplitude Modulation Signal[J]. Commun Theor Phys,2009,52 (1) :143-148.
[10]ZHANG Lingying,CAO Li,ZHU Fahui. Stochastic Resonance for Signal-modulated Pump Noise in a Single-Mode Laser[J].Chin Opt Lett,2006,4(1):30-32.
[11]陳德彝,王忠龍.噪聲間關聯程度的時間周期調制對單模激光隨機共振的影響[J].物理學報,2008,57(6):3333-3336.
[12]陳德彝,王忠龍.噪聲交叉關聯程度受時間周期調制下單模激光的光強關聯時間[J].中國激光,2009,36(1) :119-124.
[13]陳德彝,王忠龍.色噪聲間關聯的周期調制對單模激光隨機共振的影響影響[J].物理學報,2009,58(1):0102-0106.
[14]陳德彝,王忠龍.偏置信號調制下噪聲關聯的周期調制對單模激光隨機共振的影響[J].物理學報,2009,58(5):2907-2913.
[15]WANG Zhiyun,Chen Peijie,ZHANG Liangyin .The effects of Sine-Squared Pulse Modulation Correlated Noises on Stochastic Resonance in Single-Mode Laser[J].Z Naturforsch A,2011,66:411-416.
[編輯] 李啟棟
10.3969/j.issn.1673-1409(N).2012.04.003
O436
A
1673-1409(2012)04-N007-04
2012-02-27
國家自然科學基金項目(11045004)。
汪志云(1973-),男,1997年大學畢業,碩士,副教授,現主要從事激光動力學方面的教學與研究工作。

