Jacobi函數展開法與非線性Schr?dinger方程的橢圓函數解

史良馬

（巢湖學院電子工程與電氣自動化學院，安徽 巢湖 238000）

Jacobi函數展開法與非線性Schr?dinger方程的橢圓函數解

史良馬

（巢湖學院電子工程與電氣自動化學院，安徽 巢湖 238000）

利用三種基本橢圓函數來構成一般的橢圓函數，進一步推廣了橢圓函數展開法并它應用于非線性Schr?dinger方程的求解。由此得到了一系列的包絡周期解。當模數m→0或m→1時，這些解退化為孤立波解和三角函數解。

Jacobi函數；Schr?dinger方程；周期解

1 引言

非線性問題的求解是非線性科學中一項重要的工作。在求解非線性發展方程的周期解方面，自從劉式適[1-4]等提出了Jacobi函數展開法之后，人們相繼用Jacobi函數構造了各種展開法[5-7]，獲得了一些非線性發展方程的周期性精確解。本文在此基礎上提出更一般的橢圓函數展開法，我們用三種基本Jacobi函數組成一個新的函數形式，以此來構造非線性方程的解。通過這種方法可以得非線性方程豐富的周期性包絡解。并以非線性Schr?dinger方程的求解為例，說明這種方法。當模數m→0或m→1時，這些解退化為孤立波解、三角函數解。

2 構造一般Jacobi函數的展開法

對于給定非線性偏微分方程，為簡單超見以含兩個自變量為例，

P為其多變元的多項式，其中包含有非線性項和線性的高階偏導數項。

其求解步驟如下：

（1）作行波變換

其中cg為群速。代入方程，將其化為常微分方程

（2）設 u（ξ）可展為 F 有限冪級數，

其中（i,j,k,l）為（0,1,2,3）的循環順序，如當 i=0時,j,k,l分別為 3,0,1；當 i=1時，j,k,l分別為 2,3,0；當i=2時,j,k,l分別為3,0,1；當i=3時,j,k,l分別為0,1,2。

三種基本橢圓函數之間的關系：

由此可以得到下列恒等式：

式（4）中的正整數N可由具有支配地位的非線性項和最高階偏導數項的平衡[8,9]來確定。

（3）將（4）式和（5）式代入方程（3），并利用（6）、（7）、（8）和（9）式可將方程化為由橢圓函數 snξ,cnξ,dnξ組成等式，由線性無關可以得到關于a0,a1,…，aN的代數方程。

（4）解上述關于a0,a1,…，aN的代數方程可以得由方程（1）系數表示的a0,a1,…，aN，將這些結果代入（4）式得到方程（1）的周期解。在模數m→0或m→1極限情形，可以得到孤立波解和三角函數解。

3 非線性Schr?dinger方程的橢圓函數解

對于非線性 Schr?dinger（NLS）方程

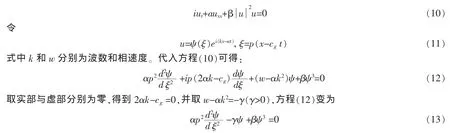
對方程（13）來說，選擇N使得非線性項和最高階偏導數項平衡，得到N=1，故由（4）式方程（13）的解可寫為：

以（5）式中 i=1,p=2 為例，

將(14)式代入方程(13)后，再利用(15)、(8)和(9)式化簡得到

4 結論

本文利用三個基本橢圓函數組成一個新的函數形式，以此來構成非線性發展方程的解，得到了一系列周期精確解，其中包括三角函數解和雙曲函數解。這種方法是一種簡單、實用而有效的求解非線性微分方程精確解的方法之一。

[1]劉式適,傅遵濤,劉式達,等.Jacobi橢圓函數展開法及其在求解非線性波動方程中的應用[J].物理學報,2001,50(11):2068-2073.

[2]劉式達,傅遵濤,劉式適,等.非線性波動方程的Jacobi橢圓函數包絡周期解[J].物理學報,2002,51(4):718-722.

[3]劉式適,付遵濤,劉式達,等.一類非線性方程的新周期解 [J].物理學報,2002,51(1):10-14.

[4]付遵濤,劉式適,劉式達.非線性波方程求解的新方法[J].物理學報,2004,53(2):343-348.

[5]劉官廳,范天佑.一般變換下的Jacobi橢圓函數展開法及應用[J].物理學報,2004,53(3):676-679.

[6]吳國將,韓家驊,史良馬，等.擴展的Jacobi橢圓函數展開法和Zakharov方程組的新的精確周期解[J].物理學報,2007,55(9):5054-5059.

[7]韓家驊,吳國將,史良馬，等.修正的雙Jacobi橢圓函數展開法及其應用 [J].安徽大學學報(自然科學版),2005,29(4):37-40].

[8]Mingliang Wang.Solitary wave solutions for variant Boussinesq equations[J].Phys.Lett.A,1995,199(3-4):169-172.

[9]Mingliang Wang.Exact solutions for a compound KdV-Burgers equation[J].Phys.Lett.A,1996,213(5-6):279-287.

GENERAL JACOBI FUNCTION EXQANSION METHOD AND PERIODIC ELLIPTIC FUNCTION SOLUTIONS OF THE NONLINEAR SCHR?DINGER EQUATION

SHI Liang-ma
（Department of Physics and Electronics,Chaohu College,Chaohu Anhui 238000）

On the basis of new function made up of three basic Jacobi,general Jacobi elliptic function expansion method is further extended and applied to solve the nonlinear Schr?dinger equation.A serial of envelope periodic solutions are obtained by this method.When modulus or these periodic solutions degenerate to the corresponding solitary wave solutions and trigonometric function solutions.

Jacobi elliptic function；Schr?dinger equation；periodic solution

O415

A

1672-2868（2012）03-0054-05

2012-03-20

安徽省教育廳年度重點基金資助項目（項目編號：kJ2012A203）；巢湖學院博士科研啟動基金資助項目

史良馬（1966-），男，安徽樅陽人。副教授，博士，研究方向：事非線性物理和凝聚態物理。

責任編輯：宏 彬