自變量優化的一元線性回歸

韓小慧，葛永慧

（太原理工大學 礦業工程學院，山西 太原030024）

自變量優化的一元線性回歸

韓小慧，葛永慧

（太原理工大學 礦業工程學院，山西 太原030024）

一元線性回歸是應用最為廣泛的參數估計方法之一。文中提出一元線性回歸的自變量在等差級數的基礎上進行雙向黃金分割，提高兩端點觀測值的多余觀測分量，縮小觀測值之間多余觀測分量的差異，在不增加觀測值數量和不改變觀測值精度的前提下，提高穩健估計方法消除或減弱粗差的能力。

一元線性回歸；穩健估計；自變量優化；雙向黃金分割

一元線性回歸是測量實際應用中最為廣泛的參數估計方法之一。但是傳統的一元線性回歸不具備抵抗粗差的能力，當測值中包含粗差時，傳統的一元線性回歸的結果便會受到歪曲［1］。而生產實踐和科學實驗所采集的數據中粗差的出現是不可避免的。為了減弱或消除粗差對參數估計的影響，G．E．P．BOX于1953年提出了穩健估計的概念。穩健估計是將估計理論建立在符合于數據實際情況的分布模式而不是建立在某種理想的分布模式［2］，許多學者就此進行了卓有成效的研究，構造了很多不同的穩健估計方法。常用的穩健估計方法有殘差絕對和最小法、Danish法、Huber法、Tukey法和IGGⅢ方案等。

一元線性回歸的自變量通常為等差級數。由于回歸方程本身的特點和自變量的設定方式決定了觀測值之間的多余觀測分量有著較大的差異，兩端點觀測值的多余觀測分量較小而中間點觀測值的多余觀測分量較大。當相同的粗差包含在不同的觀測值中時，穩健估計方法減弱或消除粗差的能力是不同的，下面用例子具體說明。

觀測值的真值（xi，yi）分別為（10，6．50），（28，15．50），（46，24．50），（64，33．50），（82，42．50），（100，51．50）。xi和yi的單位均為 m，觀測值個數n＝6，將5．0 cm粗差分別加到第1和第3個觀測值，用Danish方法計算觀測值的改正數，結果見表1。

表1中，x為自變量，y為因變量。Δ1和Δ3為真誤差。Y1和Y3分別為第1和第3個包含5．0 cm粗差的觀測值，V1和V3分別為觀測值Y1和Y3的改正數。

表1 第1和第3個觀測值包含粗差時觀測值的改正數

由表1可知，當第1個觀測值包含5．0 cm的粗差時，觀測值的改正數V1與真誤差Δ1不相同，Danish方法不能完全消除粗差對參數估計的影響。當第3個觀測值包含5．0 cm的粗差時，觀測值的改正數V3與真誤差Δ3相同，Danish方法完全消除了粗差對參數估計的影響［3］。

本文提出了自變量在等差級數的基礎上進行雙向黃金分割（通常自變量是可以人為設定的），提高了最小多余觀測分量的數值。在不增加觀測值數量和不改變觀測精度的前提下，顯著提高了一元線性回歸穩健估計方法減弱或消除粗差的效率。

1 一元線性回歸的可靠性矩陣

觀測值包含粗差時能否被發現和定位，與觀測值的多余觀測分量有著緊密的聯系，觀測值的多余觀測分量是觀測值可靠性矩陣的主對角線元素［4］。

2 自變量等差級數時的可靠性矩陣

設自變量為等差級數，公差為q，x1為首項，

設自變量x與因變量y間直線相關。觀測值為（xi，yi），i＝1，2，…，n。xi為非隨機變量，yi為隨機變量。vi為yi的殘差，＾a和＾b 為回歸系數的估值。n為觀測值個數，t＝2為參數個數，r＝n－2為自由度。

用估值表示的觀測方程為

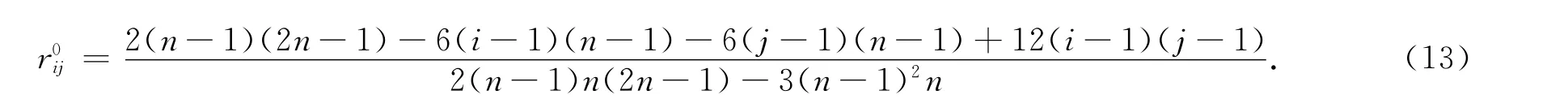
由式（13）可知，當自變量為等差級數時，可靠性矩陣與自變量的數值大小和公差的取值無關，只與觀測值的個數有關。

3 自變量雙向黃金分割時的可靠性矩陣

表2 5到9個點的自變量雙向黃金分割

當n＝6時，自變量雙向黃金分割為

x1，x1＋q－λq，x1＋q，x1＋4q，

x1＋4q＋λq，x1＋5q．

表3 自變量等差級數和自變量雙向黃金分割的可靠性矩陣主對角線元素

表3中，AP表示自變量等差級數，GS表示自變量雙向黃金分割，n表示觀測值的個數，rii表示可靠性矩陣的主對角線元素。

由表3可知，對于一定的觀測值個數，兩端點的多余觀測值分量小于中間點的多余觀測值分量，即兩端點和中間點發現和定位粗差的能力是不相同的。對于相同的觀測值個數，自變量雙向黃金分割兩端點的多余觀測值分量相對于等差級數的多余觀測值分量增加大約為0．1，減小了各個觀測值多余觀測分量之間的差異，自變量雙向黃金分割提高了兩端點發現和定位粗差的能力。

4 算 例

設直線回歸的理論方程為y＝~a＋~b~x。

取a＝1．5，b＝0．5（a和b的取值不影響計算結果），觀測值的真值為（xi，yi）（x＝1，2，…，n）。自變量xi的取值范圍為10～100。因變量yi根據自變量xi計算。xi和yi的單位均為m，自變量不同取值方式的觀測值（xi，yi）的真值如下：

自變量等差級數：（10，6．50），（28，15．50），（46，24．50），（64，33．50），（82，42．50），（100，51．50）。

自變量雙向黃金分割：（10，6．50），（17，10．00），（28，15．50），（82，42．50），（93，48．00），（100，51．50）。

對于第1個和第3個觀測值包含粗差的情況，用Danish方法計算觀測值的改正數，結果見表1和表4。用IGGⅢ方案計算觀測值的改正數，結果見表5和表6。用Tukey方法計算觀測值的改正數，結果見表7和表8。

表4 第1和第3個觀測值包含粗差時觀測值的改正數（黃金分割）

由表4可知，自變量雙向黃金分割：當第1個觀測值包含5．0 cm的粗差時，觀測值的改正數V1與真誤差Δ1相同，Danish方法完全消除了粗差對參數估計的影響。當第3個觀測值包含5．0 cm的粗差時，觀測值的改正數與真誤差相同，Danish方法完全消除了粗差對參數估計的影響。

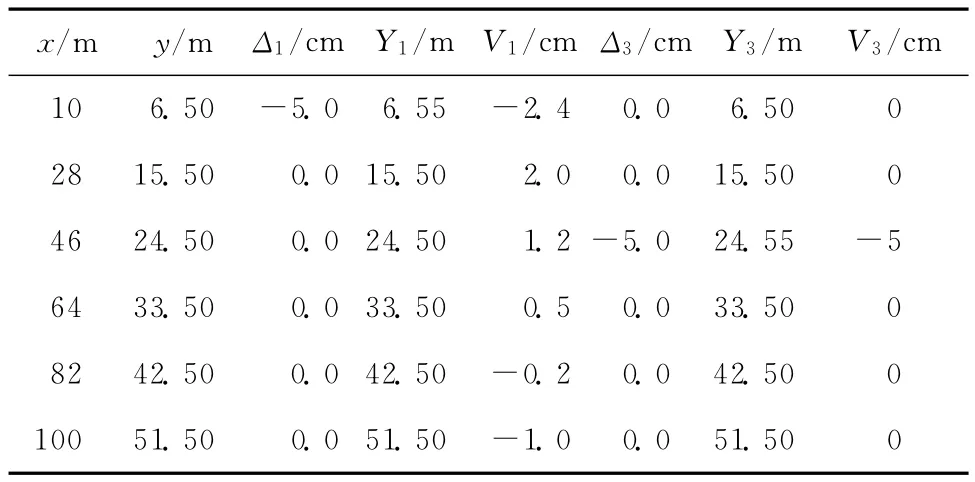
表5 第1和第3個觀測值包含粗差時觀測值的改正數（等差數列）

由表5可知，自變量等差級數：當第1個觀測值包含5．0 cm的粗差時，觀測值的改正數V1與真誤差Δ1不相同，IGGⅢ方案不能完全消除粗差對參數估計的影響。當第3個觀測值包含5．0 cm的粗差時，觀測值的改正數與真誤差相同，IGGⅢ方案完全消除了粗差對參數估計的影響。

表6 第1和第3個觀測值包含粗差時觀測值的改正數（黃金分割）

由表6可知，自變量雙向黃金分割：當第1個觀測值包含5．0 cm的粗差時，觀測值的改正數V1與真誤差Δ1相同，IGGⅢ方案完全消除了粗差對參數估計的影響。當第3個觀測值包含5．0 cm的粗差時，觀測值的改正數與真誤差相同，IGGⅢ方案完全消除了粗差對參數估計的影響。

表7 第1和第3個觀測值包含粗差時觀測值的改正數（等差數列）

由表7可知，自變量等差級數：當第1個觀測值包含5．0 cm的粗差時，觀測值的改正數V1與真誤差Δ1不相同，Tukey方法不能完全消除粗差對參數估計的影響。當第3個觀測值包含5．0 cm的粗差時，觀測值的改正數與真誤差相同，Tukey方法完全消除了粗差對參數估計的影響。

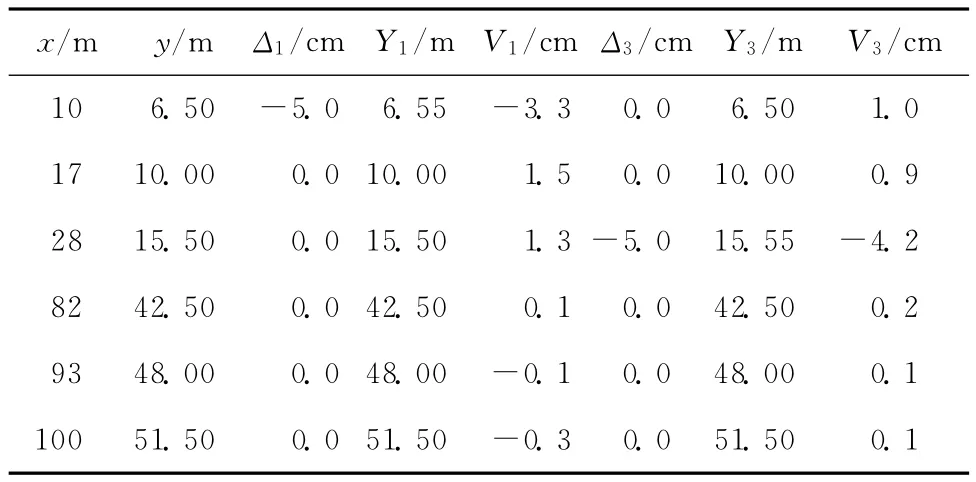
表8 第1和第3個觀測值包含粗差時觀測值的改正數（黃金分割）

由表8可知，自變量雙向黃金分割：當第1個觀測值包含5．0 cm的粗差時，觀測值的改正數V1與真誤差Δ1不相同，Tukey方法不能完全消除粗差對參數估計的影響。當第3個觀測值包含5．0 cm的粗差時，觀測值的改正數與真誤差不相同，Tukey方法同樣不能完全消除粗差對參數估計的影響。

對于自變量等差級數，當相同的粗差包含在不同的觀測值中時，穩健估計方法減弱或消除粗差的能力是不同的。例如當觀測值數量等于6和兩端點的觀測值包含粗差時，穩健估計方法不能有效地消除粗差對參數估計的影響。對于自變量雙向黃金分割，當觀測值數量等于6時，無論哪個觀測值中包含粗差，Danish方法、IGGⅢ方案和Tukey方法都能有效地消除粗差對參數估計的影響。

5 結束語

本文提出了一元線性回歸中自變量雙向黃金分割。在不改變觀測值數量和觀測值精度的前提下，自變量雙向黃金分割與自變量等差級數相比縮小了觀測值多余觀測分量之間的差異。相對于自變量等差級數，當自變量雙向黃金分割時，穩健估計方法能夠更有效地消除或減弱粗差對參數估計的影響。

［1］陳軻，歸清明，柳麗，等．Gauss－Markov模型的t型抗差估計［J］．測繪學報，2008，37（3）：280－284．

［2］王新洲 ，陶本藻，邱衛寧，等．高等測量平差［M］．北京：測繪出版社，2006：73－89．

［3］黃幼才．數據探測與抗差估計［M］．北京：測繪出版社，1990：287－309．

［4］邱衛寧，陶本藻，姚宜斌，等．測量數據處理理論與方法［M］．武漢：武漢大學出版社，2008：58－72．

［5］周江文．經典誤差理論與抗差估計［J］．測繪學報，1989，18（2）：115－120．

［6］M．I．Griep，I．N．Wakeling，P．Vankeerberghen，et al．Comparison of semirobust and robust partial least squares procedures［J］．Chemom．Intell．Lab．Syst．1995，29（1）：37－50．

［7］Peter J．Huber．Robust statistics［M］．New York：John Wiley and Sons．1981：229－236．

［8］Zioutas，G．，Avramidis，A．Deleting Outliers in Robust Regression with Mixed Integer Programming［J］．Acta Math．Appl．Sin．Engl．Ser．2005，21（2）：323－334．

［9］Peter J．Huber Robust Estimation of a Location Parameter［J］．Ann．Math．Statist．．1964，35（1）：73－101．

［10］James K．G．Watson，Robust weighting in least－squares fits［J］．J．Mol．Spectrosc．2003，219（2）：326－328．

［11］Antonia López Villavicencio，Nonlinearities or outliers in real exchange rates［J］．Economic Modelling 2008，25（4）：714－730．

Simple linear regression with independent variables optimized

HAN Xiao－hui，GE Yong－hui
（College of Mining Engineering，Taiyuan University of Technology，Taiyuan 030024，China）

Simple linear regression is one of the most widely used methods of parameter estimation．The paper proposes a bidirectional golden section based on independent variables according to arithmetical progression，which increases the redundant observations of the observations at both endpoints and narrows the difference of redundant observations among the observations．Under the premise of not increasing the number of observations and changing observation accuracy，this method improves the capability of robust estimate method eliminating and weakening gross errors．

simple linear regression；robust estimation；independent variables optimization；bidirectional golden section

P228

A

1006－7949（2012）03－0013－05

2011－05－22

國家高技術研究發展計劃（863計劃）資助項目（2008AA06A415－06A4）

韓小慧（1986－），女，碩士研究生．

［責任編輯劉文霞］