區間數級數的理論研究

高德寶

（黑龍江八一農墾大學理學院，大慶 163319）

區間數級數的理論研究

高德寶

（黑龍江八一農墾大學理學院，大慶 163319）

文章在已知實數項級數收斂及區間數列收斂概念的基礎上，具體闡述了區間數項級數的定義及其性質.然后，給出了幾個關于正區間數項級數斂散性判斷定理與推論.最后，關于一般項區間數級數斂散性的判別作了討論.

區間數；級數；收斂；發散

1 引 言

區間分析或稱區間數學是最近四十年來發展起來的一個新的數學分支.目前，區間分析的主要研究對象是區間數的應用，而關于區間數以及區間數集的研究卻很少.文獻［1，2］給出了區間數的定義及其基本運算，介紹了區間數在計算方法、自動控制中的具體應用.雖然，區間分析學的有關理論已被越來越多地應用到各個領域，如文［3，4］，但它的基礎性理論還有很大的研究空間.本文基于文獻［1，2，5，6，7］，結合數學分析的相關理論，給出區間數級數收斂的定義以及多個判別方法.

2 區間數的概念及其基本運算

定義1 稱A＝［al，ar］為一個區間數.當al＝ar時，區間數就退化為一實數.

定義2 給定兩個區間數A＝［al，ar］，B＝［bl，br］，兩個區間數之間有如下的運算

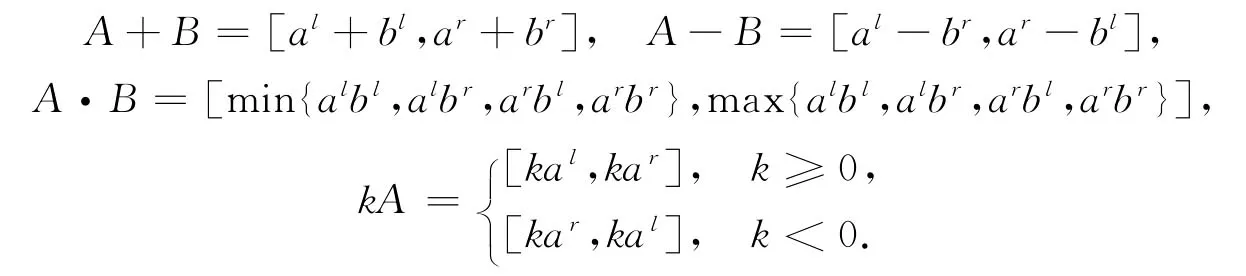
上面所提及的理論基本上來源于文獻［3］.相應于正數、負數與實數的模的定義，我們給出區間數對應的定義.

定義3 給定一個區間數［x，y］.若x＞0，稱其為正區間數.若y＜0，稱其為負區間數.

定義4 給定一個區間數［x，y］.對于所有的t∈［x，y］，稱由所構成的閉區間為區間數［x，y］的模，記作｜［x，y］｜.

由上面的定義，可得計算公式

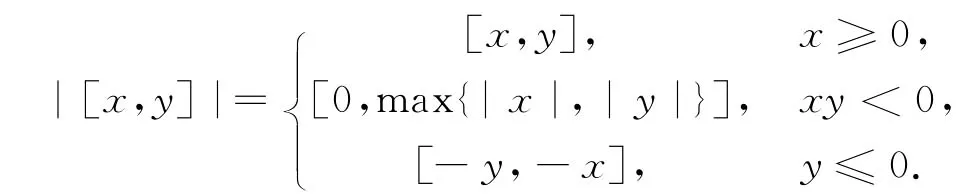
定義5 設｛［an，bn］｝為一區間數列，若存在一實數M＞0，使得

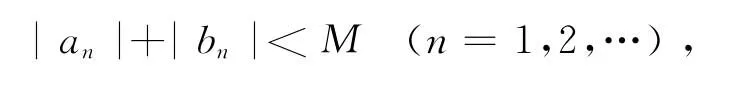
則稱其為有界區間數列.

定義6 設｛［an，bn］｝為區間數列，若an≤an＋1，bn≤bn＋1，則稱其為單調遞增區間數列；若an≥an＋1，bn≥bn＋1，則稱其為單調遞減區間數列.

定義7 設｛［an，bn］｝為區間數列，［a，b］為區間常數.若對任給的正數ε，總存在正整數N，使得當n＞N時，有｜an-a｜＋｜bn-b｜＜ε.則稱區間數列｛［an，bn］｝收斂于［a，b］，常數［a，b］稱為區間數列｛［an，bn］｝的極限，并記作［an，bn］＝［a，b］.若區間數列｛［an，bn］｝沒有極限，則稱其不收斂，或稱其為發散數列.

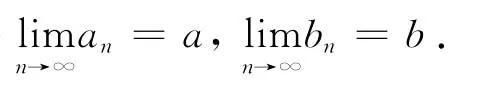
3 區間數級數的收斂性

定義8 給定一個區間數列｛［an，bn］｝，對它的各項依次用“＋”號連接起來的表達式

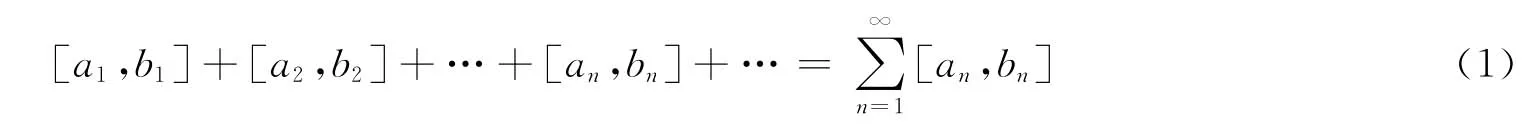
稱為區間數項無窮級數或區間數項級數（可簡稱為區間數級數），其中［an，bn］稱為區間數項級數的（1）通項或一般項.區間數項級數（1）也可簡單寫作∑［an，bn］.

區間數級數（1）的前n項之和，記為

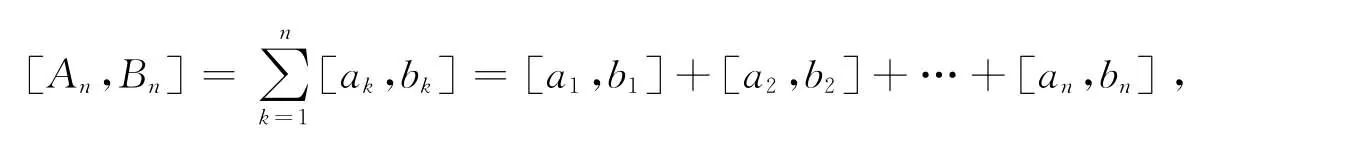
稱它為區間數項級數（1）的第n個部分和，簡稱部分和.

定義9 若區間數項級數（1）的部分和數列｛［An，Bn］｝收斂于［A，B］，則稱區間數項級數（1）收斂，稱［A，B］為區間數項級數（1）的和，記作

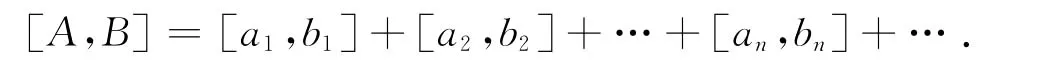
若｛［An，Bn］｝是發散區間數列，則稱區間數項級數（1）發散.

根據區間數列極限的定義，有下面的定理.

定理2 區間數項級數∑［an，bn］收斂的充要條件是：實數項級數∑an，∑bn（an≤bn）收斂.

推論區間數項級數∑［an，bn］發散的充要條件是：實數項級數∑an或∑bn（an≤bn）發散.

定理3 區間級數（1）收斂的充要條件是：任給正數ε＞0，總存在正整數N，使得當m＞N以及對任意的正整數p，都有

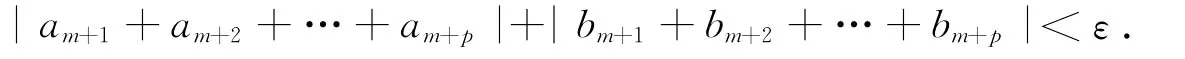
推論若級數（1）收斂，則

定理4（線性運算） 若區間數級數∑［an，bn］與∑［cn，dn］都收斂，則對任意的實常數k，l，級數∑k［an，bn］＋l［cn，dn］亦收斂，且

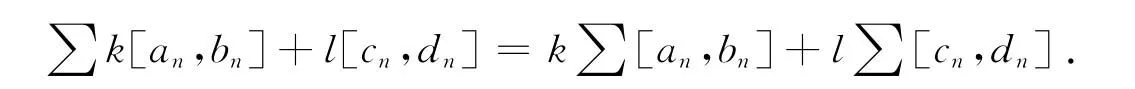
定理5 去掉、增加或改變級數的有限項并不改變級數的斂散性.

定理6 在收斂級數的項中任意加括號，既不改變級數的收斂性，也不改變它的和.

4 正區間數項級數

若區間數項級數各項均是正區間數或均是負區間數，則稱它為同號級數.對于同號級數，只需研究各項都是由正區間數組成的級數——稱為正區間項級數.如果級數的各項都是負數，則它乘以-1后就得到一個正區間項級數，它們具有相同的斂散性.

定理7 正區間數項級數∑［an，bn］收斂的充要條件是：實數項數列｛Bn｝有界，即存在某正數M，對一切正整數n有Bn≤M.

對于正區間項級（1）而言，因為an≤bn，若∑bn收斂，則∑an必收斂；若∑an發散，則∑bn必發散.故對于其收斂性而言，我們只需討論∑bn收斂性.而正數項級∑bn收斂性的充要條件是它的部分和數列有界.故定理7易證.定理7與下面的兩個定理是等價的.

定理8 正區間數項級數∑［an，bn］收斂的充要條件是正項級數∑bn收斂.

推論正區間數項級數∑［an，bn］發散的充要條件是實數項級數∑an發散.

定理9 設∑［an，bn］是正區間項級數，∑cn是正項級數.如果存在某正整數N，對一切n＞N都有

（i）bn≤cn且∑cn收斂，則正區間數項級數∑［an，bn］收斂.

（ii）cn≤an且∑cn發散，則正區間數級數∑［an，bn］發散.

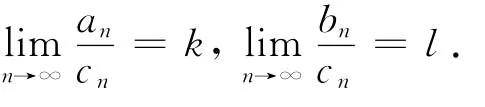
（i）當0＜l＜＋∞時，級數∑［an，bn］和級數∑cn同時收斂或同時發散.

（ii）當k＝0且級數∑cn發散時，級數∑［an，bn］發散.

（iii）當k＝＋∞或l＝＋∞且級數∑cn發散，則級數∑［an，bn］也發散.

證根據數學分析［5］中的比較原則，當0＜l＜＋∞時，級數∑bn和級數∑cn同時收斂或同時發散，故根據定理8可得：結論（i）是成立的.當k＝0且級數∑cn發散時，級數∑an是發散的，根據定理8的推論可知：結論（ii）是成立的.當k＝＋∞或l＝＋∞且級數∑cn發散時，級數∑an或∑bn發散，故結論（iii）是成立的.

（i）當q＜1時，正區間項級數∑［an，bn］收斂.

（ii）當q＞1或p＞1時，正區間項級數∑［an，bn］發散.

定理11（根式判別法） 設∑［an，bn］是正區間項級數，且存在某正整數N及常數l，

（i）若對一切n＞N，成立不等式nbn≤l＜1，則正區間項級數∑［an，bn］收斂；

（ii）若對一切n＞N，成立不等式nbn≥1，則正區間項級數∑［an，bn］發散.

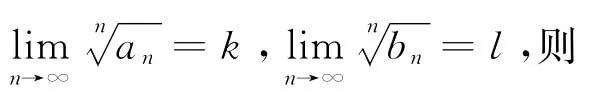
（i）當l＜1時，正區間項級數∑［an，bn］收斂；

（ii）當k＞1或l＞1時，正區間項級數∑［an，bn］發散.

4 一般項區間數級數

定義10 若區間數項級數的正、負區間數相間，即

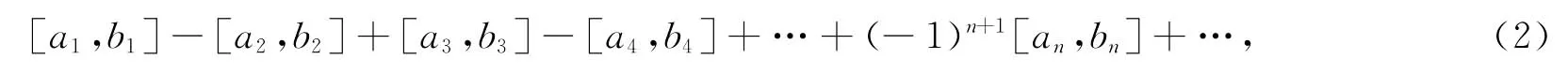
則稱其為為交錯區間數級數.

定理12（萊布尼茲判別法） 若交錯區間數級數（2）滿足下述兩個條件：

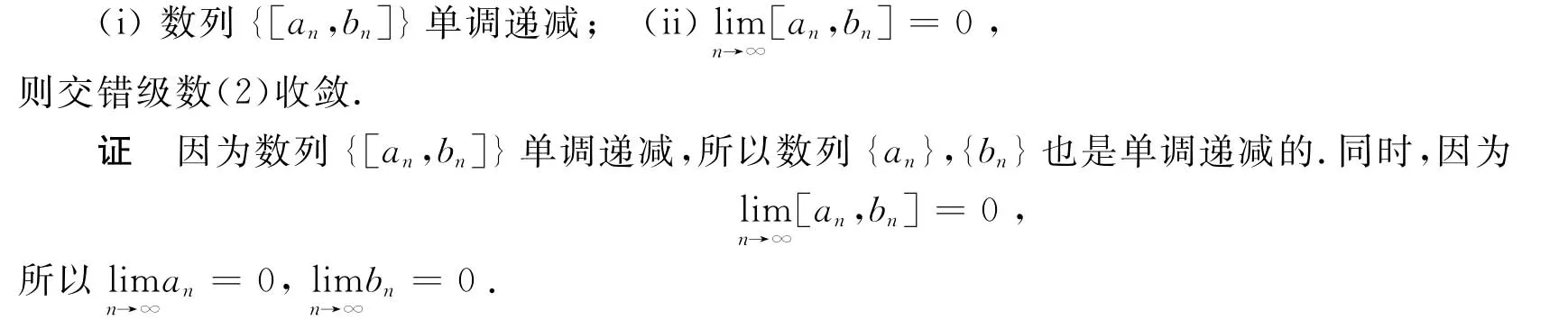
根據數學分析［5］中的萊布尼茲定理，數項級數∑（-1）n-1an，∑（-1）n-1bn是收斂的.故交錯區間數項級數（2）是收斂的.

推論若區間數級數（2）滿足萊布尼茲判別法的條件，則收斂的區間數級數（2）的余項估計式為

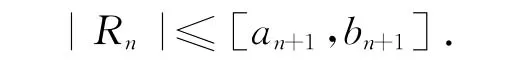
定義11 若區間數項級數［a1，b1］＋［a2，b2］＋…＋［an，bn］＋…的各項絕對值所組成的級數

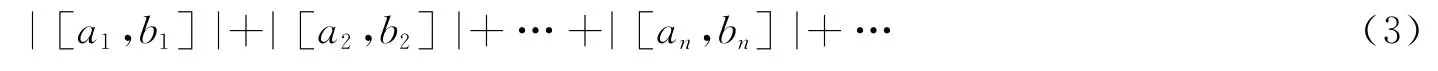
收斂，則稱原區間項級數為絕對收斂級數.

定理13 絕對收斂的區間數項級數一定收斂.

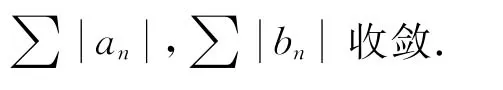
故級數∑an，∑bn是收斂的，從而級數∑［an，bn］是收斂的.

由區間數的乘法運算，我們會得到如下兩個區間數列乘積的級數：

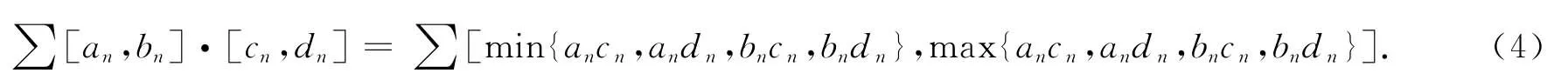
定理14（阿貝爾判別法） 若｛［an，bn］｝為單調遞增（或遞減）的有界區間數列，且區間數項級數∑［cn，dn］收斂，則區間數項級數（4）收斂.

證因為｛［an，bn］｝為單調遞增（或遞減）的有界區間數列，所以數列｛an｝，｛bn｝是單調遞增（遞減）且有界的.因為區間數項級數∑［cn，dn］收斂，所以數項級數∑cn，∑dn是收斂的.

根據數學分析［5］中的阿貝爾判別法可知，四個數項級數

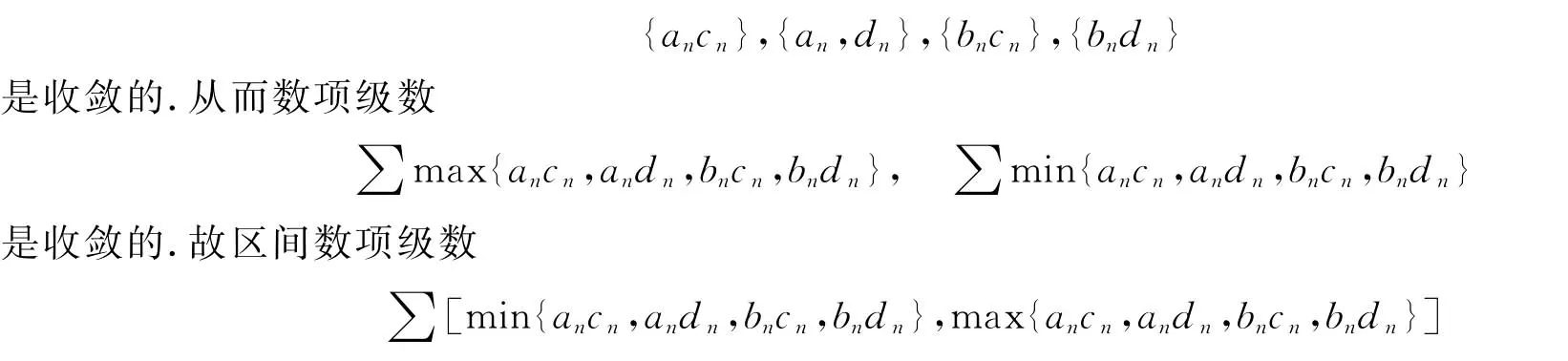
是收斂的.即區間數項級數（4）是收斂的.

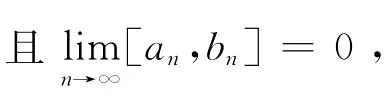
此定理的證明過程需用數學分析［5］中的狄利克雷判別法定理，它的證明過程與定理14的基本相同.故其證明過程略.

［1］ Moore R E.Interval analysis［M］.Englewood：Prentice-Hall，1966.

［2］ Moore R E，Kearfott R B，Cloud M J.Introduction to Interval Analysis［M］.SIAM：2008.

［3］ Chen P Y.An interval estimation for the number of signals［J］.Signal Processing，2005，85（3）：1622-1633.

［4］ Hansen E.Global Optimization Using Interval Analysis the Multi-Dimensional Case［J］.Numerische Mathematik，1980，34（3）：247-270.

［5］ Chen C Z.Mathematical Analysis［M］.Higher Education Press：2005.

［6］ Seqngupta A，Pal K.On comparing interval numbers［J］.European Journal of Operation Research，2000，127（1）：28-43.

［7］ Chanas S，Zielinski P.Ranking fuzzy interval numbers in the Setting of random sets-further results［J］.Information Scienee，1999，117（8）：201-207.

Study on The Theory of Interval Series

GAO De-bao
（College of Sciences，Heilongjiang Bayi Agricultural University，Daqing 163319，China）

The definition and its properties of interval number series is described in detail，which is based on the concepts of real series and interval sequences.Then，it gives a few theorems and deductions of the convergence and divegence of positive interval number series.At last，the he convergence and divergence of the common interval numbers series is discussed.

interval number；series；convergence；divergence

O173.1

A

1672-1454（2012）03-0042-05

2009-11-07