滾塑成型工藝加熱階段的數值研究

劉學軍

（北京工商大學材料與機械工程學院，北京100048）

0 前言

滾塑工藝的成型周期主要受外部環境與模具的對流換熱、內部空氣和塑料粉末的混合物與模具的對流換熱、塑料層的熔融與固化相變等多方面的影響。為此，對滾塑成型工藝建立一個準確的流動與傳熱的理論模型，然后通過數值計算對其進行模擬就顯得尤為重要。這種數值模擬可以研究多個滾塑參數對其成型周期的影響，從而為滾塑成型工藝的最優化提供理論依據。

郭同凱［1］和高鐿等［2］分別為滾塑成型工藝建立了傳熱模型。但都沒有給出任何理論分析解或數值計算結果。高桂天等［3］為卡車翼子板的滾塑成型工藝建立了一個簡單的一維熱傳導及熔融相變的傳熱模型。他們根據這個模型給出了加熱時間的理論計算結果，并將其與實驗結果相比較。何躍龍等［4］對一個圓柱形塑料制品的滾塑工藝建立了一維的傳熱模型。根據該模型給出了模具加熱時間、塑料粉末熔融燒結時間以及溫度場的理論分析解。

Gogos等［5］對一個球形中空制品的滾塑成型工藝的加熱階段建立了一維瞬態的傳熱模型，利用有限差分法對其進行了真正的數值計算。在該模型里，他們假設塑料粉末是均勻混合的。在加熱階段，塑料粉末只有一個作為集總參數的溫度在隨時間變化。計算區域只包含模具本身，不包括塑料粉末和內部空氣，但在模具內壁面處建立了模具與塑料粉末之間的熱平衡方程。筆者認為該傳熱模型有以下幾個方面需要改進：（1）塑料粉末的導熱率比較小，因此忽略其內部熱阻對其采用集總參數法會產生較大的誤差。（2）由于計算區域不包括內部空氣，因此該模型無法計算出加熱階段內部空氣的溫度。（3）該模型需要估計模具內部的對流換熱系數，這帶有較大的不確定性。

本文將對球形中空塑料制品的滾塑成型工藝的加熱階段建立一個更接近于實際的傳熱模型。在這個模型里，計算區域將擴大到包括模具、黏附在模具內壁面的塑料粉末層以及內部空氣，這樣內部空氣的溫度隨時間的變化規律也就可以計算出來。由于這是耦合換熱，因此模型中不再出現內部的熱邊界條件，內部的對流換熱系數也就不再需要估計。本文將利用有限容積法通過Fluent軟件對文獻［6］中的三種實驗條件進行數值模擬，并將計算結果與該文獻中的實驗結果進行比較，以驗證本模型的準確性。最后再應用此模型分別對不同外部加熱溫度、外部對流換熱系數以及塑料粉末層厚度的情形進行數值計算，以研究這些參數對滾塑成型工藝加熱時間的影響，并得出了一些有益的結論。

1 流動與傳熱模型

本模型假設在整個滾塑成型過程中，塑料粉末總是緊密地貼附在模具內壁面上形成一層均勻的塑料導熱層。即不考慮塑料粉末以及隨后熔融塑料的流動，但考慮內部空氣的流動。這個假設與實際情況之間具有一定的偏差，本文后面將此模型的計算結果與實驗結果相比較可以證明該假設所帶來的誤差在工程上仍是可以接受的。如圖1所示，本模型的計算區域包括模具、塑料粉末層以及內部空氣，將模具的導熱、塑料粉末層的導熱和隨后的熔融以及內部空氣的自然對流換熱耦合起來求解。考慮到此球形計算區域沿經度方向的對稱性，因此這是一個二維瞬態的傳熱學問題，即所有的計算物理量都是時間坐標t和空間坐標（r，θ）的函數。

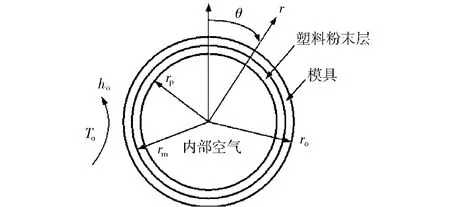
圖1 滾塑成型工藝加熱階段的流動與傳熱模型Fig.1 Heat transfer and fluid flow model of heating phase of rotational molding

對于模具，其控制方程是二維瞬態的導熱方程。外壁面（ro）的邊界條件為第三類熱邊界條件，內壁面（rm）的邊界條件為熱流密度連續條件。對于塑料層，其控制方程也是二維瞬態的導熱方程。內、外壁面（rp，rm）的邊界條件均為熱流密度連續條件。塑料層的熔融相變將采用Enthalpy-porosity方法來計算。這種方法不直接跟蹤熔融界面的移動，而是根據熵平衡在每一次迭代中計算液態相的百分比（介于0和1之間）。詳細內容可參見文獻［7］。

對于內部空氣，其流動和傳熱模式為自然對流換熱。控制方程為二維瞬態層流的連續性方程、動量方程和能量方程。其壁面（rp）上采用無滑移速度邊界條件和熱流密度連續條件。在以上所有方程中除內部空氣的密度之外，均采用常物性假設。考慮到在整個加熱過程中，內部空氣的溫度變化比較大，為保證計算結果的準確性，本模型不采用自然對流的Boussinesq假設，而是把內部空氣當成是密度隨溫度變化的理想氣體。

2 計算參數的確定

筆者將采用本文的理論模型去數值模擬文獻［6］中的3種實驗條件，如表1所示。

表1 計算的3個實驗條件Tab.1 Three experimental conditions calculated

在對以上3個實驗條件進行數值模擬時，本文將采用與文獻［6］完全相同的物性參數、結構參數以及工藝參數（如表2所示）以保證計算結果與實驗結果的可比性。

3 Fluent軟件的設置

在Fluent應用程序中選擇瞬態的二維平面層流模型，并選擇melting／solidification模塊。在設置環境條件時，需要將豎直方向上的加速度設為-9.8m／s2以考慮內部空氣自然對流的影響。在設置空氣物性時，要選擇理想氣體。計算采用SIMPLE算法［8］。為保證瞬態問題數值解的穩定性，在沿時間方向上的差分格式采用一階全隱格式。關于松弛因子，壓力項采用0.3，密度項、體積力項和能量項都采用1，動量項采用0.5，液態相百分比采用0.8。時間步長設為5s，每一個時刻的迭代次數設為90次。計算結果表明90次的迭代可保證每一個時刻的速度殘差不超過10-3，溫度殘差不超過10-9，且熔融開始后，塑料層中液態相百分比的相對變化不會超過千分之一。

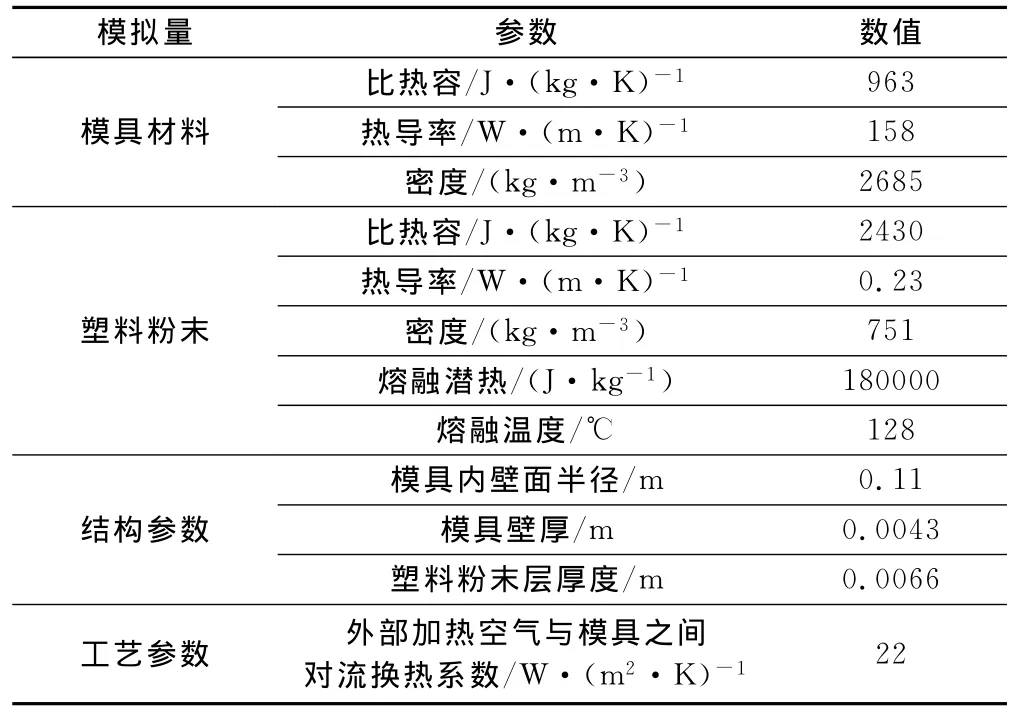
表2 數值模擬所采用的參數Tab.2 Parameters for numerical simulation

在迭代計算過程中，當模具內壁面溫度升高到塑料粉末的熔融溫度時，液態相的百分比開始大于0，這表明塑料粉末開始熔融。隨后液態相的百分比隨時間越來越大。當其值達到1時，說明全部塑料粉末都已經熔融完畢，加熱過程結束，此時即可終止迭代。

4 數值計算結果及分析

4.1 計算結果與實驗結果的比較

首先應用本文的理論模型對表1所列的三種實驗條件進行數值模擬。表3中給出了本文模型計算所得的加熱時間與文獻［6］中實驗所得的加熱時間相比較的結果。加熱時間是指從裝有塑料粉末的模具在加熱室里開始受熱直到所有塑料粉末都已熔融沉積在模具內壁面為止所花費的時間。

從表3中可以看出對于加熱時間來說，本模型的計算結果與文獻［6］中的實驗結果吻合得較好。在3種實驗條件下，最大的相對誤差不超過9%，在文獻［3］中，理論加熱時間與實際加熱時間的相對誤差為13.8%，仍認為在工程允許的范圍內，本文計算的相對誤差更小，從而證明了本文模型的準確性。從該表還可以看出計算所得的加熱時間比實測的加熱時間都要短，本文認為造成該誤差的主要有兩個原因：（1）本文假設自始至終塑料粉末都均勻緊密地黏貼在模具的內壁面上，這樣塑料粉末與模具內壁面之間始終是以純導熱方式來進行傳熱。但實際的情況是塑料粉末和內部空氣的混合物與模具內壁面進行對流換熱。因為該對流換熱是在一個封閉空腔內進行的，因此其換熱系數很小，不會超過5W／（m2·K）［5-6］。也就是說，本文的模型在一定程度上過分地強化了模具內壁面向塑料粉末的傳熱，因此使得計算所得的加熱過程提前結束。（2）文獻［6］通過一套測量系統來連續地監測模具內部的空氣溫度。當該空氣溫度開始急劇增大，即認為所有的塑料粉末已經完全熔融沉積，此時所測得的時間即為整個加熱過程所花費的時間。本文認為用這樣的方法來判斷塑料粉末完成熔融在時間上可能有一定的滯后，也就是說文獻［6］所測得的加熱時間可能比實際值要稍微長一些。

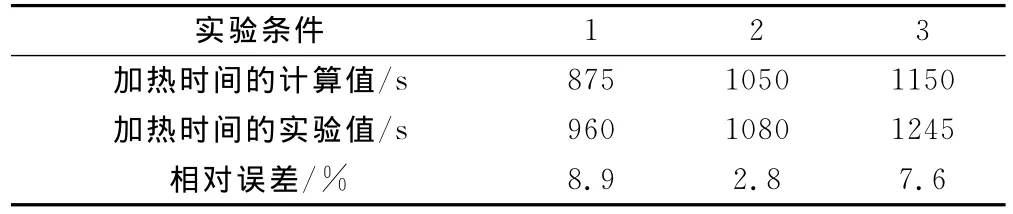
表3 加熱時間的計算值與實驗值的比較Tab.3 Comparison of calculated results of heating time with experimental results

圖2 模具外壁面溫度的計算值與實測值的比較Fig.2 Comparison of calculated values with experimental values of mold temperatures

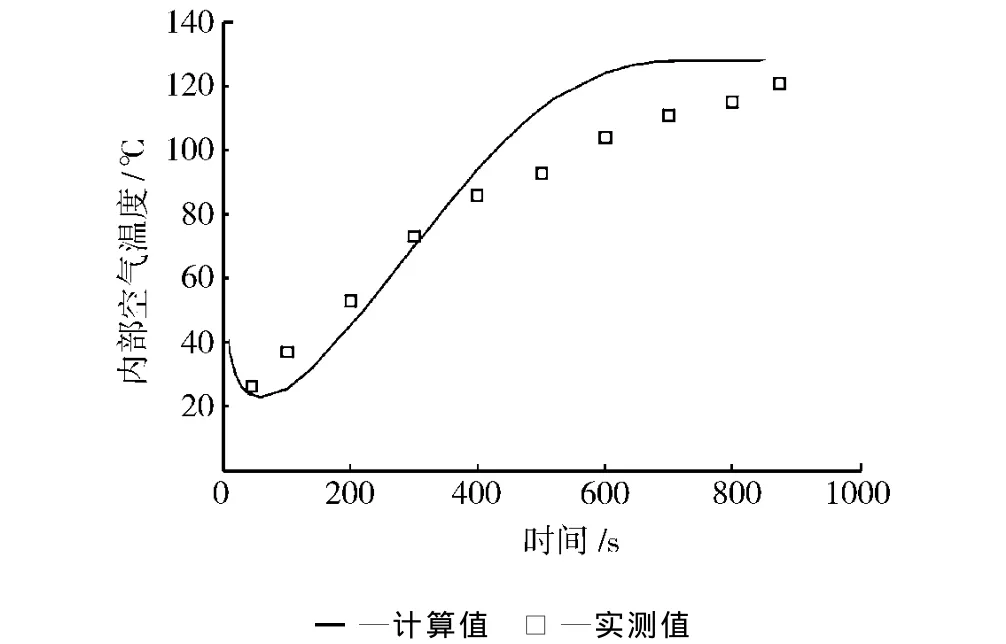
圖3 內部空氣溫度的計算值與實測值的比較Fig.3 Comparison of calculated values with experimetal values of internal air temperatures

圖2和圖3分別顯示了對于實驗條件1，本模型計算所得的模具外壁面溫度和內部空氣溫度與文獻［6］中相應的實測值相比較的結果。可以看出這兩個溫度的數值計算結果與實驗結果吻合得也比較好，這從另一個側面進一步證實了本文理論模型的準確性。從圖2可以看出，模具外壁面溫度的計算值在整個加熱過程都要低于實測值。造成這個誤差的主要原因可能還是如前所述。在本文模型中，模具的內壁面與塑料粉末層總保持緊密接觸，即模具與塑料粉末層之間的熱阻比實際情況偏小。因此在加熱過程中就有更多的熱量傳給了塑料粉末層和內部空氣，而留給模具本身的熱量相對較少，因此計算出來的模具溫度就比實際值偏低一些。而獲得較多熱量的塑料粉末層則能更快地完成熔融，從而使得理論上的加熱過程比實際提前結束。另外同樣也獲得較多熱量的內部空氣理論上溫升就會較快，這也解釋了為什么在圖3中內部空氣溫度的計算值隨時間增大的速率要高于實測值。但在加熱過程的最后大約300s，該計算值隨時間增大的很慢，無限地趨近于塑料粉末的熔融溫度128℃，這一點也與實測的內部空氣溫度隨時間的變化規律有一些差別。對于實驗條件2和3，從表3可以看出其加熱時間的計算值與實測值之間的相對誤差比實驗條件1更小，因此可以推斷其模具外壁面溫度和內部空氣溫度的計算值與實測值之間應該都吻合得比實驗條件1更好，對這兩個實驗條件就沒必要再做上述的比較。

4.2 外部加熱溫度和對流換熱系數對加熱時間的影響

首先采用與表2中完全相同的計算參數，只是將加熱溫度從250℃增大到380℃，把數值模擬的結果畫在圖4中以表示外部加熱溫度對滾塑工藝加熱時間的影響。從圖4可以看出加熱時間隨加熱溫度的增大而減少，但在加熱溫度超過300℃后，加熱時間隨加熱溫度的增大而減少的速度變得越來越慢。也就是說，盡管提高外部加熱溫度確實可以縮短滾塑工藝的加熱時間，但在加熱溫度超過300℃后，該措施的有效性就變得越來越差。實際上如果加熱溫度太高，塑料粉末就容易發生氧化，致使滾塑制品的力學性能變差。因此從加熱的有效性以及力學性能的強化這兩方面來綜合考慮，合適的外部加熱溫度應該是300℃左右。

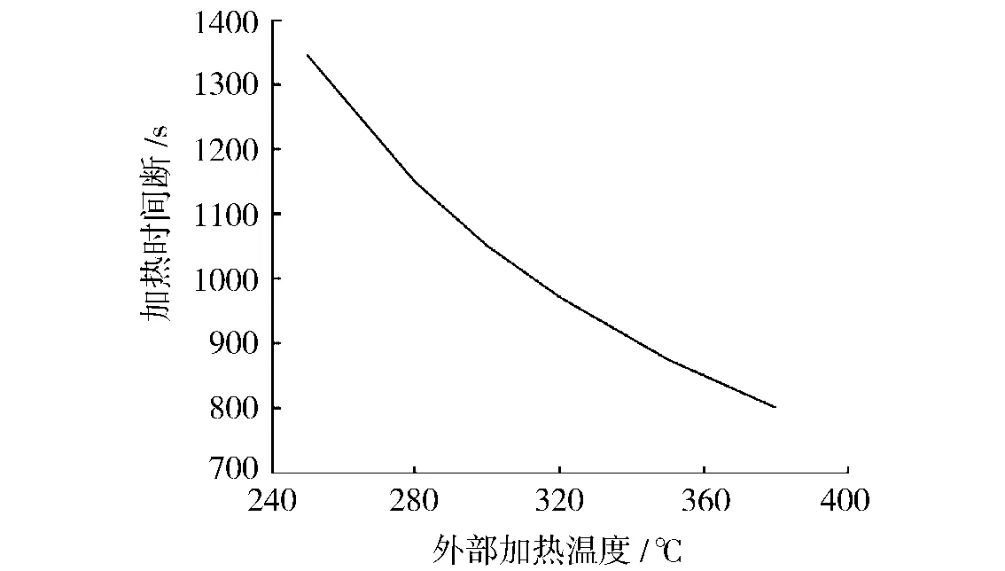
圖4 加熱時間隨外部加熱溫度的變化Fig.4 Variation of heating time with outer heating temperature

加熱時間（t）由兩部分組成，一部分是將模具從室溫加熱到塑料粉末熔融溫度所花費的時間（t1），另一部分是塑料粉末從剛開始熔融到全部完成熔融所花費的時間（t2）。很顯然t＝t1＋t2。上述計算結果表明對于加熱 溫 度 250 ℃ 的 情 形，t1／t ＝ 48.3%，t2／t＝51.7%；對于加熱溫度380 ℃的情形，t1／t＝41.2%，t2／t＝58.8%。通過兩種情形的對比可以發現隨著加熱溫度的提高，塑料粉末的熔融時間在整個加熱時間中所占的百分比明顯增加。這說明造成高溫加熱有效性變差的主要因素是塑料粉末的熔融過程拖累了整個加熱過程的結束。這可能是由于在較高的加熱溫度下，更多的熱量被模具吸收走，而留給塑料粉末用于熔融的熱量卻增加的不多，致使整個熔融過程不能很快結束。總而言之不能單純地通過提高外部加熱溫度來縮短滾塑工藝的加熱時間，而要采取一些其他的輔助措施。比如可以在塑料粉末開始熔融的時候，采用模具內部加熱的方法來加快塑料粉末的熔融過程。

接著本文采用與表2相同的計算參數，將外部加熱溫度定為300℃，將外部對流換熱系數從18W／（m2·K）依次增大到28W／（m2·K），把數值模擬的結果畫在圖5中以表示外部對流換熱系數對滾塑工藝加熱時間的影響。從該圖可以看出加熱時間隨外部對流換熱系數的增大而減少，但在對流換熱系數超過22 W／（m2·K）之后，加熱時間隨之減少的速度也開始逐步放緩。但與圖4相比，可以看出圖5中曲線的彎曲程度并不嚴重，這說明采用增大外部對流換熱系數的方法比采用提高外部加熱溫度的方法能更有效地縮短滾塑工藝的加熱時間。可以通過改變外部加熱方式、改進模具的表面結構等措施來提高外部對流換熱系數。

4.3 塑料粉末層厚度對加熱時間的影響

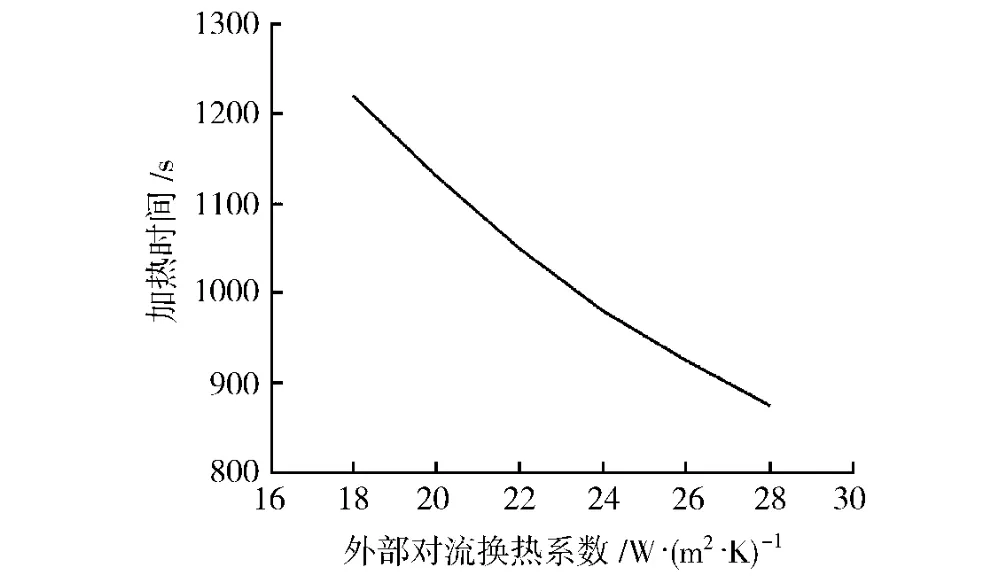
圖5 加熱時間隨外部對流換熱系數的變化Fig.5 Variation of heating time with outer convective heat transfer coefficient

采用與表2完全相同的計算參數，并將加熱溫度保持為300℃。然后應用本文計算模型分別對不同的塑料粉末層厚度的情形進行數值模擬，將其結果畫在圖6中以表示滾塑成型工藝的加熱時間隨塑料粉末層厚度的變化規律。從該圖可以看出隨著塑料粉末層厚度的增大，需要的加熱時間也越來越長。另外還可以看出圖中曲線的斜率越變越大，這說明加熱時間并不按線性關系隨塑料粉末層厚度增加，而是隨該厚度以越來越快的速度急劇增加。也就是說對于厚度較大的塑料制品，其滾塑成型工藝的時間成本會增大很多，因此滾塑成型的塑料制品的厚度應設計得盡可能的小。但另一方面，為提高塑料制品的強度，又希望其厚度能比較大。所以采用滾塑成型工藝的設計者應綜合考慮塑料制品的成本及強度這兩方面的要求才能確定合適的塑料制品厚度。

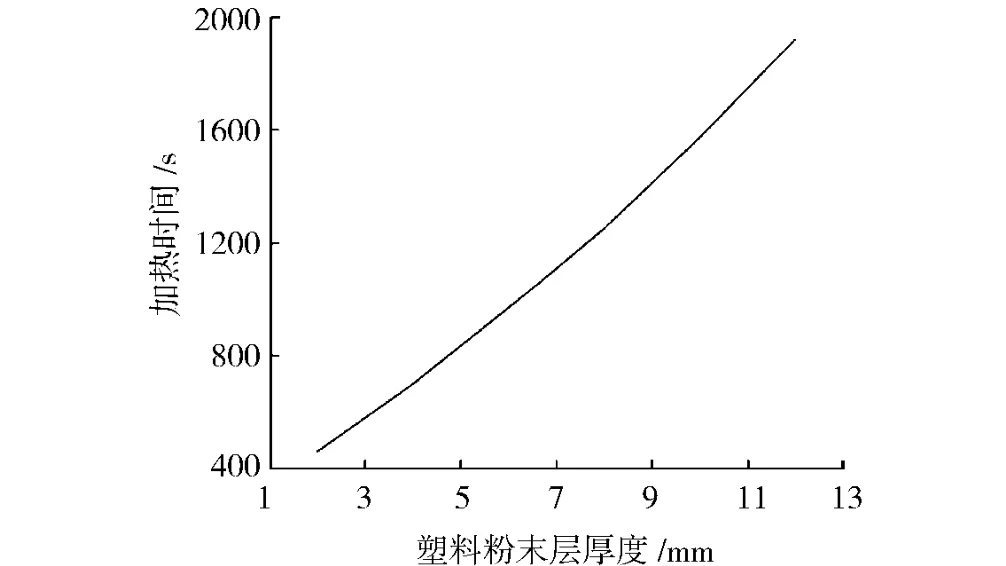
圖6 加熱時間隨塑料粉末層厚度的變化Fig.6 Variation of heating time with thickness of plastic powder layer

5 結論

（1）本文為滾塑成型工藝的加熱階段建立了一個新的理論模型。該模型將模具的導熱、塑料粉末層的導熱和隨后的熔融相變，以及內部空氣的自然對流換熱耦合起來求解。在該模型中，采用有限容積法并通過Fluent軟件對滾塑成型工藝的加熱階段進行了數值模擬。計算所得的加熱時間、模具溫度和內部空氣溫度與文獻［6］中的實驗結果都吻合得較好，從而驗證了本文理論模型的正確性。

（2）提高外部加熱溫度可以縮短滾塑成型工藝的加熱時間。但在加熱溫度達到300℃時，繼續增大外部加熱溫度，加熱時間減少的速度明顯變慢，即通過提高加熱溫度來縮短加熱時間的有效性開始變差。

（3）增大外部對流換熱系數也可以縮短滾塑成型工藝的加熱時間。但在對流換熱系數超過22W／（m2·K）之后，加熱時間隨之減少的速度開始逐步放緩。與提高外部加熱溫度相比，增大外部對流換熱系數能更有效地縮短加熱時間。

（4）隨著塑料制品厚度的增大，滾塑成型工藝的加熱時間會急劇增加，即采用滾塑工藝的制造成本會大大增加。

［1］郭同凱.旋轉模塑過程的熱交換計算機模擬系統［J］.新技術新工藝，1997，（3）：7-9.Guo Tongkai.Heat Transfer Computer-simulating System of Rotational Molding Process［J］.New Technology and Process，1997，（3）：7-9.

［2］高 鐿，王福生，高幼銀.滾塑成型工藝中的傳熱模型［C］.2005中國國際滾塑論壇論文集，2005：62-66.

［3］高桂天，梁 策，史新星，等.滾塑成型加熱時間的計算［J］.吉林大學學報（工學版），2008，38（2）：340-343.Gao Guitian，Liang Ce，Shi Xinxing，et al.Heating Time Algorithm for Rotational Molding［J］.Journal of Jilin University（Engineering and Technology Edition），2008，38（2）：340-343.

［4］何躍龍，丁玉梅，李維維.單軸滾塑成型傳熱過程的數學建模［J］.塑料科技，2009，37（5）：35-39.He Yuelong，Ding Yumei，Li Weiwei.Mathematical Model of Heat Transfer During Rotational Molding of Single Axis［J］，Plastics Science and Technology，2009，37（5）：35-39.

［5］Gogos G，Olson L G，Liu Xuejun，et al.New Models for Rotational Molding of Plastics［J］.Polymer Engineering and Science，1998，38（9）：1387-1398.

［6］Olson L G，Crawford R，Kearns M，et al.Rotational Molding of Plastics：Comparison of Simulation and Experimental Results for an Axisymmetric Mold［J］.Polymer Engineering and Science，2000，40（8）：1758-1764.

［7］Voller V R，Prakash C.A Fixed-grid Numerical Modeling Methodology for Convection-diffusion Mushy Region Phase-change Problems［J］.Int J Heat Mass Transfer，1987，30（8）：1709-1719.

［8］陶文銓.數值傳熱學［M］.西安：西安交通大學出版社，2001：203-207.