一種圓環(huán)面刀具五坐標端銑加工局部干涉檢測算法

譚建新

(婁底職業(yè)技術(shù)學院機電工程系，湖南婁底 417000）

0 引言

復雜曲面在航空航天、汽車、輪船及模具行業(yè)中得到了廣泛應用，這些曲面通常需要依靠五坐標數(shù)控銑削加工來完成，其中刀具與工件曲面的干涉檢測一直是該領域的重點和難點之一，國內(nèi)外很多學者對此進行了研究。通常刀具與工件曲面的干涉可分為局部過切和全局干涉兩類。其中，局部過切代表刀具刀頭部分和工件曲面在局部范圍內(nèi)的干涉，而全局干涉是指刀柄與工件及夾具等的干涉。目前，已有的干涉檢測方法主要有多面體法［1］、直接距離計算法［2-4］、刀具與曲面離散法［5-6］、凸包法［7-9］及其它專用算法［10-11］等。由于刀具類型及曲面加工形式的不同，幾乎所有的算法都有一定的應用局限性。針對圓環(huán)面刀具和端銑刀，陳麗萍等［4］提出了一種局部過切檢測算法，該方法利用賦范空間投影算法求圓環(huán)面刀具環(huán)心圓到工件曲面的最小距離來進行干涉檢測，算法簡單且計算效率高。龔堰玨等［12］指出這種賦范投影算法對于復雜曲線曲面可能存在發(fā)散的情況，由此提出了一種改進的幾何迭代算法。基于此，本文借鑒了這種思想，提出了一種穩(wěn)定易收斂的適用于圓環(huán)面刀具五坐標端銑加工的局部干涉檢測算法，并通過一個例子對算法的正確性和有效性進行了驗證。

1 圓環(huán)面刀具五坐標端銑加工特性

在復雜曲面端銑加工領域中，刀位算法一直是研究的熱點和難點。刀位算法被用來確定刀具相對于工件曲面的位置，目的是使刀具與工件曲面在不發(fā)生過切的前提下從工件毛坯中去除盡可能多的材料。目前應用最廣泛的刀位算法是刀軸傾斜法，它已經(jīng)作為通用算法被集成到商業(yè)軟件如UG、Mastercam中。對于球頭刀五坐標端銑加工而言，只需要根據(jù)刀觸點處法矢量和刀具半徑即可求得刀心點坐標，刀軸矢量也可由法矢量和進給方向來簡單確定，而圓環(huán)面刀具則要復雜的多。

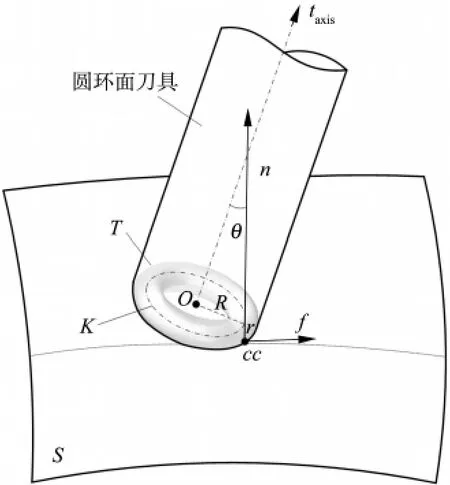
圖1 圓環(huán)面刀具端銑加工

圖1為用圓環(huán)面刀具進行曲面端銑加工的示意圖，其中S代表工件曲面，T代表圓環(huán)面刀具的工作切削面即圓環(huán)面，K代表T的環(huán)心圓，O為T的幾何中心，R和r分別代表T的環(huán)心圓半徑和圓角小半徑。cc代表一條刀路軌跡上圓環(huán)面刀具和工件曲面S之間的切觸點，n代表工件曲面S在cc點處的法矢量，f代表刀具進給方向，taxis代表圓環(huán)面刀具的刀軸矢量。根據(jù)圓環(huán)面的空間幾何性質(zhì)，容易知道法矢量n和環(huán)心圓K一定是相交的。基于刀軸傾斜法基本原理，刀軸矢量taxis一定位于由切觸點處法矢量n和刀具進給方向f確定的平面內(nèi)且與n的夾角為θ，則可以確定圓環(huán)面刀具的定位，其中θ被稱為Sturz角。

刀軸傾斜法傾向于使用固定的角度θ來完成整個曲面加工所需刀位處的刀具定位，由于曲面的復雜性，在一些刀位處，刀具和曲面的局部干涉是不可避免的，因此需要針對每個刀位處進行局部干涉檢測，然后通過調(diào)整角度θ來得到?jīng)]有局部干涉的優(yōu)化刀位。圓環(huán)面刀具端銑加工局部干涉檢測問題實際上是刀具圓環(huán)面和工件曲面之間的面面關系。為了簡化問題，可將圓環(huán)面刀具與理想曲面的幾何相對關系簡化為刀具環(huán)心圓K到工件曲面S的最小距離問題。用lmin代表該最小距離，當lmin小于圓角小半徑r時，圓環(huán)面刀具和工件曲面S之間發(fā)生了局部干涉，此時最大干涉量dmax可以通過dmax=r-lmin計算出來。根據(jù)dmax可以進行刀位調(diào)整從而得到無局部干涉的刀位，因此圓環(huán)面刀具曲面端銑加工的局部干涉檢測問題就轉(zhuǎn)化成計算K到S的最小距離問題。

2 局部干涉檢測算法原理

2.1 算法原理

在圖2中，N0、N1和 N 為曲面 S上的點，M0、M1和M為刀具環(huán)心圓K上的點，t0、t1和t分別代表環(huán)心圓K在M0、M1和M 處的參數(shù)，t0、t1和 t分別代表刀具環(huán)心圓K在點M0、M1和M處的切矢量，Δt代表刀具環(huán)心圓K上相鄰迭代點間參數(shù)t的增量。圓環(huán)面刀具局部干涉檢測算法的具體實現(xiàn)步驟如下:

(1）將刀具環(huán)心圓K按照參數(shù)t均勻離散，分別求該10個離散點到曲面S的最小距離，將使得距離最小時曲線曲面上的點位信息作為初始迭代信息:點 M0、N0、切向量 t0和參數(shù) t;

(2）把問題考慮為求曲面上點N0到刀具環(huán)心圓K的最小距離問題，此時將M0看作刀具環(huán)心圓K上的初始迭代點，根據(jù)點到曲線最小距離算法容易得到迭代步長Δt，根據(jù)t1=t0+Δt得到刀具環(huán)心圓K上的新迭代點M1和新的切向量t1，調(diào)用求點到曲面最小距離算法，可以得到點M1在曲面上的投影點N1;

(3）重復以上過程，經(jīng)過若干次迭代，當|Δt|＜10-6時停止，程序結(jié)束。

此時刀具環(huán)心圓K上的點收斂于點M，MN垂直于曲線在點M處的切向量t，同時點N為點M在曲面S上的投影，因此MN的長度即為算法所求的最短距離。

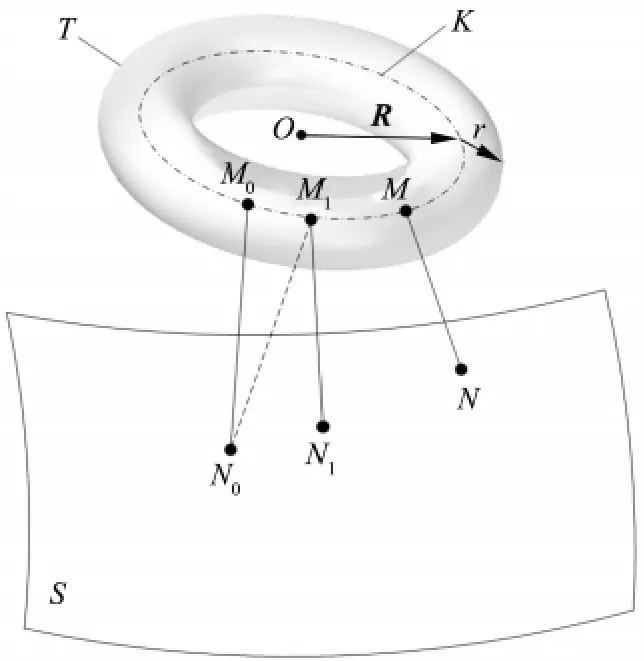
圖2 圓環(huán)面刀具局部干涉檢測算法

2.2 刀位修正處理

利用上述所提出的算法對整個曲面所有刀位進行局部干涉檢測，對于存在局部干涉的刀位，必須進行刀位修正。刀位修正的基本思想是調(diào)整圓環(huán)面刀具的刀軸矢量即調(diào)整刀具后跟角θ，從而避免刀具和加工表面的局部干涉。刀位修正過程可以通過迭代判斷來實現(xiàn)。

3 計算點到曲面的最小距離

由上可知，圓環(huán)面刀具局部干涉檢測算法是通過輪流求點到曲線最小距離和點到曲面最小距離來完成的，而這些都是可以通過賦范空間投影幾何迭代算法來實現(xiàn)，這兩種幾何迭代算法同時具有效率高且穩(wěn)定的特點。點到曲線的最小距離算法相對簡單，下面介紹一下點到曲面的最小距離算法。

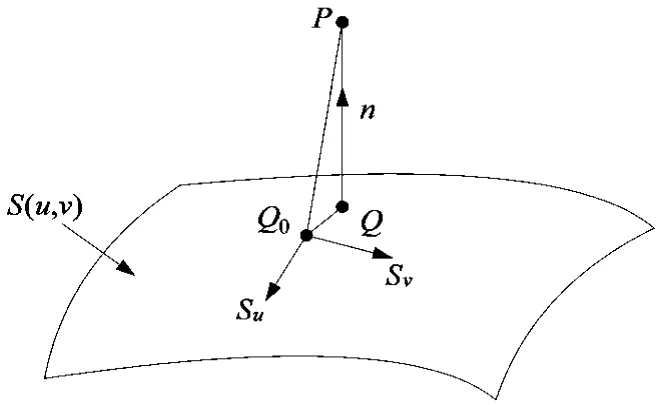
圖3 空間點到曲面最小距離迭代算法

在圖3中，空間一點P，Su和Sv分別是曲面S在初始迭代點Q0的兩個關于參數(shù)u和v的偏導數(shù)，假定曲面是正則的，則在任意點處兩個偏導數(shù)的叉積不等于零。則迭代步長Δu和Δv可以通過下面的方程組計算出來。

其中E、F和G為曲面S在點Q0處的第一基本量。計算出Δu和Δv以后，將得到的曲面上的新點作為新的初始迭代點，重復以上過程，直到|Δu|＜10-6及|Δv|＜10-6同時滿足時停止，此時即可求得精度要求范圍內(nèi)P點在曲面S上的投影點Q。

4 算法實例

選用雙參數(shù)曲面S(u，v）來驗證本文所提出的局部干涉檢測與修正方法，它的曲面方程由下式?jīng)Q定。

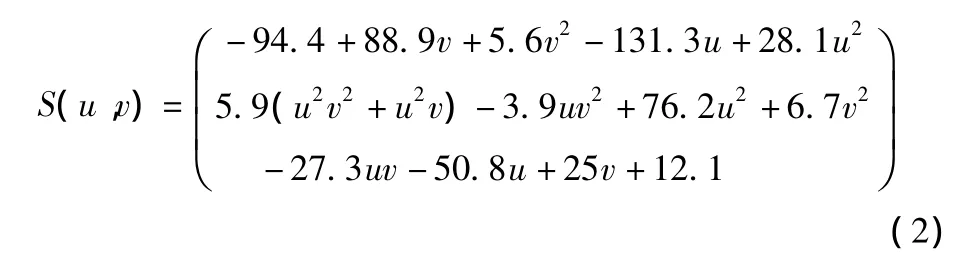
圓環(huán)面刀具參數(shù)為:R=10mm和r=3mm。使刀具進給方向f與曲面v參數(shù)一致。已知在由參數(shù)(u，v）=(0.5，0.5）決定的刀位處，有刀具傾斜角θ=5.118，利用本文提出的局部干涉檢測算法對該刀位進行檢測，可以得到使得圓環(huán)面刀具環(huán)心圓K到參數(shù)曲面S(u，v）達到最小距離時的對應點，有:M(-53.22，-64.73，17.09）和 N(-52.71，-65.47，14.34），如圖4所示，最小距離lmin可以計算出來，為lmin=2.8996mm。由于lmin＜r，可以判定圓環(huán)面刀具和參數(shù)曲面S(u，v）在該刀位處發(fā)生了干涉，且干涉量dmax=r-lmin=0.1004mm。此時需要調(diào)整刀軸矢量即調(diào)整θ角的大小對該刀位處進行修正處理。通過迭代判斷，得到當θ=5.847時，lmin=3.000mm，此時局部干涉可以得到有效的避免。

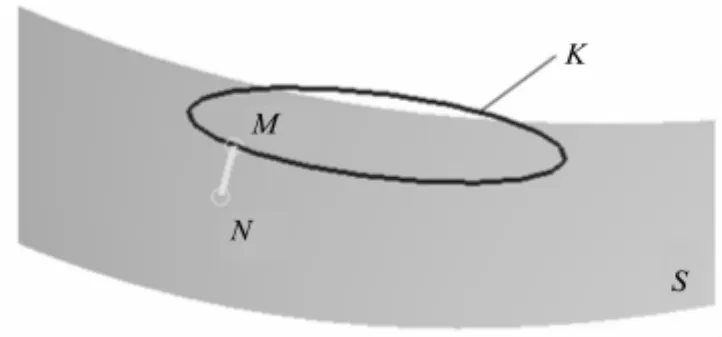
圖4 局部干涉算法的驗證

表1給出了用本文提出的局部干涉算法對不同刀位處進行檢測的情況，其中θ代表了初始給定的刀具后傾角，θ終代表最終確定的最優(yōu)刀具后傾角，tcal為檢測需要的時間，這可以通過連續(xù)運行5000次取平均值來獲得，采用C語言編程，在PC機(主頻為1.8G，內(nèi)存512M）上運算。

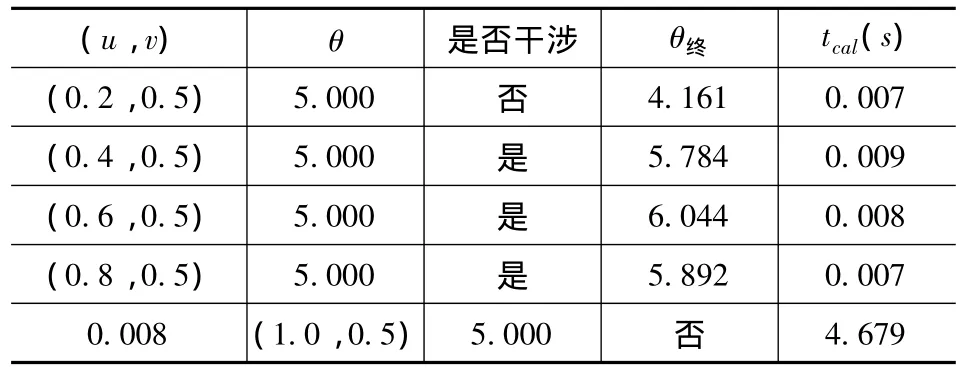
表1 一些刀位處的干涉檢測情況

容易看出，在參數(shù)(u，v）等于(0.2，0.5）和(1.0，0.5）處，干涉沒有發(fā)生，說明刀具后跟角θ還可以更小，以使刀具和工件曲面之間獲得更好的幾何匹配;而在參數(shù)(u，v）等于(0.4，0.5）、(0.6，0.5）和(0.8，0.5）處，經(jīng)檢測干涉已經(jīng)發(fā)生，說明需要增大刀具后跟角才可以，θ終值能夠真實的反映這個情況。同時，本文提出的干涉檢測算法具有很高的計算效率，這五個刀位的平均檢測時間為0.0078s。

5 結(jié)束語

在分析圓環(huán)面刀具五坐標端銑加工特性的基礎上，本文提出了一種新的局部干涉檢測算法。算法首先求得圓環(huán)面刀具環(huán)心圓到理想曲面之間的最小距離，然后將該距離與圓環(huán)面刀具的圓角小半徑比較，從而判斷局部干涉是否發(fā)生，并對發(fā)生干涉刀位通過調(diào)整刀軸矢量進行了處理。所提出的算法具有很高的計算效率，可以明顯的節(jié)省計算機運行時間，具有較高的工程應用價值。

［1］陳松，姜虹，李學藝，等.自由曲面五坐標數(shù)控加工干涉檢查［J］.工程圖學學報，2003(3）:31-36.

［2］蔡永林，席光，樊宏周，等.曲面5軸加工中全局干涉檢查與刀位修正［J］.機械工程學報，2002，38(9）:131-135.

［3］陳麗萍，陳燕，胡德金.非球頭刀數(shù)控加工無干涉刀位的計算方法［J］.上海交通大學學報，2004，38(7）:1130-1133.

［4］嚴思杰，周云飛，陳學東，等.五軸NC加工干涉檢查與避免算法研究［J］.中國機械工程，2006，17(17）:1822-1825.

［5］張和明，張玉云，熊光楞.復雜曲面五坐標數(shù)控加工干涉檢查與刀位修正［J］.清華大學學報(自然科學版），1998，38(2）:65-68.

［6］彭芳瑜，周云飛，周濟.復雜曲面的無干涉刀位軌跡生成［J］.華中科技大學學報(自然科學版），2002，30(2）:1-4.

［7］LEE Y S，CHANG T C.2-Phase approach to global tool interference avoidancein 5-axis machining［J］.Computer-Aided Design，1995，27(10）:715-729.

［8］高峰，吳俊軍，王同洋，等.基于包容盒分解的快速干涉檢驗算法［J］.計算機輔助幾何設計與圖形學學報，2000，12(6）:435-440.

［9］許曉光.5坐標加工中干涉檢測的凸包算法研究［J］.航空精密制造技術(shù)，2008，44(6）:28-32.

［10］楊方飛，閻楚良，林洪義.五軸數(shù)控加工葉片無干涉刀位軌跡的計算［J］.農(nóng)業(yè)機械學報，2003，34(2）:97-100.

［11］姜虹，于源，王小椿.復雜腔槽五軸數(shù)控加工的干涉檢查及修正算法研究［J］.機械科學與技術(shù)，2007，26(3）:274-278.

［12］龔堰玨，贠敏，王小椿.自由曲線曲面距離迭代算法的研究及其可視化處理［J］.小型微型計算機系統(tǒng)，2003，24(12）:2306-2308.