水資源危機預警模型

秦 成

(中國煤炭科工集團重慶研究院，重慶 400039)

水資源危機是指水資源系統不能保證生態、經濟和社會可持續利用及其發展，并且供求矛盾異常尖銳時的狀態[1]。水資源危機涉及的誘因較多，存在明顯不確定性，但爆發前的水資源系統狀態的變化卻是一個按客觀規律演變的連續變化過程，水危機的發生只是該系統連續變化過程中符合客觀科學規律的一個突變[2]。

從水資源危機發生前各種危機前兆的出現，到問題積聚到某一程度引發水資源危機這一過程存在一定的時間間隔，因此可以在這個時間段內通過預警來提前預報危機并采取相應措施控制或減緩危機的產生。所以預警的研究對解決水資源危機問題有著至關重要的作用，并成為當前研究的熱點。陳紹金[3]建立了基于系統動力學的湘江流域水安全系統預警模型;文俊等[4]提出了基于熵組合權重的區域水資源可持續利用預警新模型;李仰斌等[5]進行了山西省水資源安全評價與預警研究。但是，當前的研究還存在3個關鍵問題:①目前常用的預警方法將會面對預警警界即閾值難確定的問題，很多文獻是根據實際經驗確定閾值，缺乏理論依據;②面對預警指標眾多、指標間非線性關系復雜的難題，如何篩選合適的預警指標以及如何預測指標在未來時段的量值;③傳統的預警方法需要建立精準的數學模型方可實現對未來狀態的預測，然而面對像水資源系統這樣不確定或非線性時，此類方法就難以實現。為此，筆者將粗糙集(rough set)理論引入到水資源危機預警研究中，利用決策表的屬性約簡來篩選預警指標并獲得預警判別規則，在此基礎之上通過BP神經網絡預測預警指標未來的值，然后帶入預警判別規則即可快速而簡便地完成水資源危機預警。

1 CC-RS-BP模型的建立

1.1 系列年水資源危機識別

劉梅[2]和申海亮[6]分別驗證了水資源系統具有突跳性、多徑性、發散性和可恢復性，符合突變理論的基本應用條件，因此可以把尖點突變(cusp catastrophe)模型應用到水資源系統危機識別中[2，6]。

尖點突變模型勢函數是

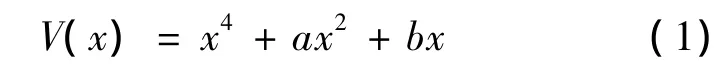
式中:x為狀態變量，a和b為控制變量，故相空間是三維的。

勢函數的所有臨界點集合成突變流形M，其表達式為V'(x)=4x3+2ax+b，通過聯立V'=0和V″=0可得到反映狀態變量與各控制變量間關系的分歧集Δ，Δ是突變流形M在控制空間a～b平面上的投影:

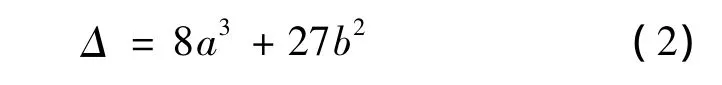
在平衡曲面M中發生質變有2種基本形式:①漸變。當a＞0時，b的變化只引起狀態變量x的光滑變化，x連續的從上葉量變過渡到下葉或由下葉量變過渡到上葉，b稱為正則因子;②突變。當a＜0時，M上出現褶皺，x的變化不再連續，a、b達到分歧集方程關系時，x從上葉突跳到下葉或由下葉突跳到上葉，a稱為剖分因子。在尖點突變中，a是決定突變的力量，b是某種質態的保守力量[7]。

因此，在應用突變模型前首先要確定控制變量。一般來說，水資源危機識別因子錯綜復雜又相互關聯，如果分析每個因子，不僅增加工作量，而且分析是孤立的，如果盲目減少因子又會損失很多信息。所以尋求一個合理的方法成為解決問題的關鍵。筆者采用主成分分析法，在保證數據信息丟失最少的前提下，把反映人類活動對水資源系統不利影響的識別因子 I1，I2，…，In－k進行主成分提取，得到少數幾個主成分，對這幾個主成分加權求和得到綜合主成分，將其作為尖點突變模型的剖分因子a。同樣把反映水資源系統自身狀態的識別因子In－k+1，…，In進行主成分分析，求得綜合主成分將其作為尖點突變模型的正則因子b。狀態變量x是指水資源系統的狀態。將各年a、b的值帶入式(2)，若Δ＜0，說明水資源系統將會發生突變。分歧集值Δ與控制變量a和b直接相關，而a和b又是從整個水資源系統出發通過主成分分析得到的，因此分歧集值Δ代表著水資源系統內部各個子系統綜合作用的結果。這就是說，水資源系統中某個或某幾個子系統出現了問題，可能并不會影響整個系統正常運行，當各子系統之間相互碰撞，不利因素突顯出來，便會導致系統狀態發生突跳，即爆發水資源危機[2]。

1.2 決策表的建立和離散化數據

設S={U，A，V，f}為一知識表達系統，U為對象的非空有限集合，稱為論域;A=C∪D是屬性集合，子集C和子集D分別稱為條件屬性和決策屬性;V是對象屬性的值域;f是信息函數，指定每個對象屬性的屬性值。具有條件屬性和決策屬性的知識表達系統稱為決策表。本次研究中將水資源危機識別的結果作為決策屬性，識別因子作為條件屬性。決策表以1個二維表格的形式表示。表中的每1列描述了1個屬性(識別因子)，每1行描述了所研究論域中的1個樣本。

粗糙集理論易于處理離散數據，然而在實際的水資源系統中大多數指標數據都是連續的。因此要實現連續數據的粗糙集約簡處理，得到水資源危機識別規則知識，其前提就是要將連續數據進行離散化。目前對連續數據進行離散化的方法有多種:等距離劃分、等頻率劃等，但是使用這些方法需用戶對數據特征有較清楚的認識[8]，所以本文采用具有動態聚類特性和一定的自適應性的K-均值聚類算法對連續數據進行離散化。

1.3 屬性約簡

在選取的各種水資源危機識別因子中，并非所有的因子都很重要，其中某些屬性是冗余的。屬性約簡就是在保持屬性分類能力不變的條件下，刪除其中不相關或不重要的屬性。對?a∈C，若posC(D)=pos(C－{a})(D)(posC(D)稱為 D 的 C正域)則認為a是冗余的，稱C'=C－{a}為C的一個約簡。通過屬性約簡后保留的指標即為預警指標。

1.4 水資源危機識別決策規則產生及過濾

令Xi和Yj分別代表U/C與U/D中的各個等價類，des(Xi)表示對等價類Xi的描述，即等價類Xi對于各條件屬性值的特定取值;des(Yj)表示對等價類Yj的描述，即等價類Yj對于各決策屬性值的特定取值。決策規則定義如下:

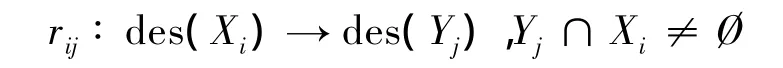
根據約簡后的決策信息系統，可以得到具有一定決策概率的不精確決策規則。其中大量的決策規則是冗余的，這就需要衡量這些規則的價值。從系統客觀層面評價一條規則，主要依據可信度、覆蓋率和支持數來衡量，在數據挖掘時，一般希望得到可信度和覆蓋率都高的有效規則，但實際上這兩個指標是成負關系的。所以需要權衡一規則的可信度和覆蓋率來評價其價值。雖然運用數學方法可以對一規則進行評價，但還應結合水資源科學的相關知識、考慮水資源危機自身的特點。

1.5 BP神經網絡滾動預測預警指標值

由于預警指標歷史樣本數目N往往較小，故一般只能對各指標進行短中期預測。在確定BP網絡拓撲結構時，網絡輸入層和輸出層的神經元節點數均取預警指標數目，隱層的神經元節點數往往需要根據設計者的經驗和多次試驗來確定。用BP神經網絡模型進行滾動預測的基本思想就是[9]:設xi為一系統因子數據系列，i=1，2，…，N，在進行神經網絡預測時用 xi－n，xi－n+1，…，xi－1的信息數據來預測 i時刻的值，即將 xi－n，xi－n+1，…，xi－1作為數據信息輸入，而xi的值作為預測的期望值，以此構造如下學習樣本:輸入(x1，x2，…，xn)輸出 xn+1;輸入(x2，x3，…，xn+1)輸出 xn+2…;輸入(xN－n，xN－n+1，…，xN－1)輸出xN。通過對學習樣本的訓練，直到誤差達到允許的范圍，就可以用它滾動預測預警指標值。

1.6 水資源危機預警

將預測得到的預警指標數據樣本根據決策規則對水資源危機狀況進行判別，可能出現以下某種情況:①一個數據樣本與一個規則相匹配;②一個數據樣本與一個以上規則相匹配，結果一致;③一個數據樣本與一個以上規則相匹配，但結果不一致;④一個數據樣本不與任何一個規則相匹配。對于情況①和②，規則的判定結果是一致的;對于情況③和④可采用少數推理方法[10]來消除不一致沖突問題。應用這種推理方法，對于任意待識樣本都可以根據從決策表中所得到的規則進行判別，得到合適的結論。

2 實例研究

本文以A市為例，在文獻[11]的基礎上，針對水資源危機的特點篩選如下識別因子:I1為GDP年增長率，%;I2為人口自然增長率，%;I3為萬元GDP產值耗水量，m3/萬元;I4為萬元產值工業耗水量，m3/萬元;I5為農田灌溉用水定額，m3/hm2;I6為水資源開發利用程度，%;I7為地表水綜合污染指數;I8為地下水位下降速率，m/a;I9為人均占有水資源量，m3/人;I10為地表水資源模數，萬m3/(km2·a);I11為地下水可開采資源模數，萬m3/(km2·a)。為了進行系列年水資源危機識別，所有的識別因子都包含了1998—2007年10 a的數據，如表1所示。

采用 spss17 統計分析軟件分別對 I1、I2、I3、I4、I5、I6、I7、I8和 I9、I10、I1111 個評價因子進行主成分抽取，先將指標在方向統一為越大越好的值，再將各個指標值進行標準化處理，取得標準化值Z。對Z1，Z2，Z3，Z4，Z5，Z6，Z7，Z88 個表現人類活動對水資源系統影響的標準化變量進行分析，得到3個主成分F1、F2、F3，方差計算表明，累計方差貢獻率達到93.1%，認為能夠很好地代表原始數據，由F1、F2、F3加權求和得綜合主成分a(其代表人類活動對水資源系統影響，是決定突變的力量)，將它作為尖點突變模型的剖分因子。對Z9、Z10、Z113個表現自然水資源狀態的標準化變量進行分析，抽取累計方差貢獻率達93.7%的兩個主成分 W1、W2，由 W1、W2計算綜合主成分b(其代表水資源自然狀態，是保守力量)，將它作為尖點突變模型的正則因子。各年的剖分因子、正則因子計算結果如表2所示。

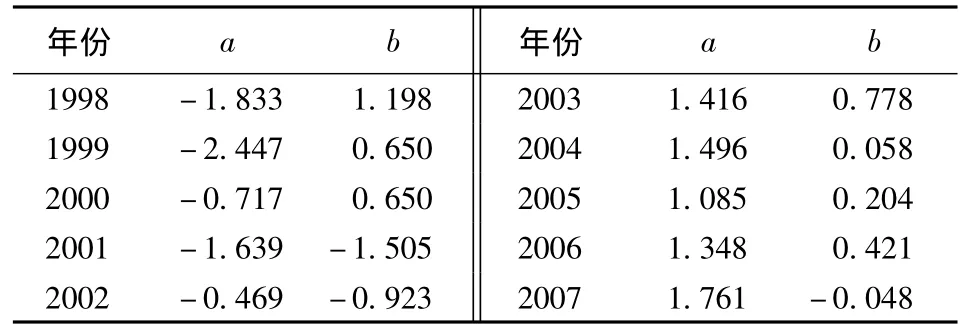
表2 系列年a、b值

將a、b值帶入式(2)進行計算，可知Δ＜0的是1998年和1999年，水資源系統處于不穩定狀態，將會發生突跳，即水資源系統處于危機狀態。其他年份Δ＞0，水資源系統處于穩定狀態，發生漸變。在決策表中決策屬性取值按Δ＜0取0，Δ＞0取1。決策屬性取值按Δ＜0取0，Δ＞0取1，即，0代表危機狀態，1代表非危機狀態，見表3所示。

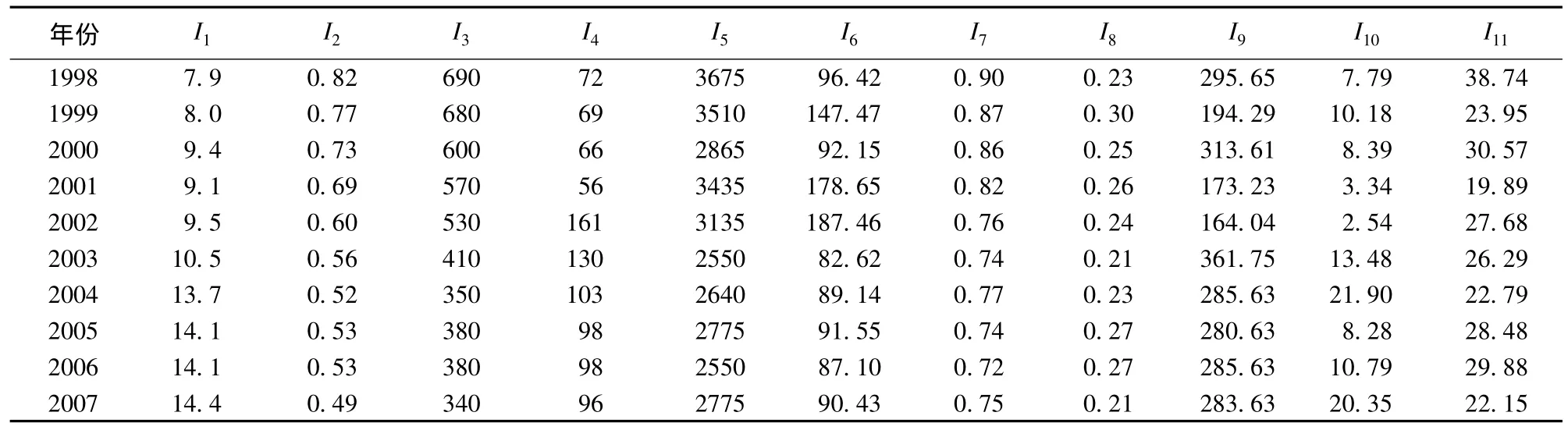
表1 水資源危機識別因子原始數據

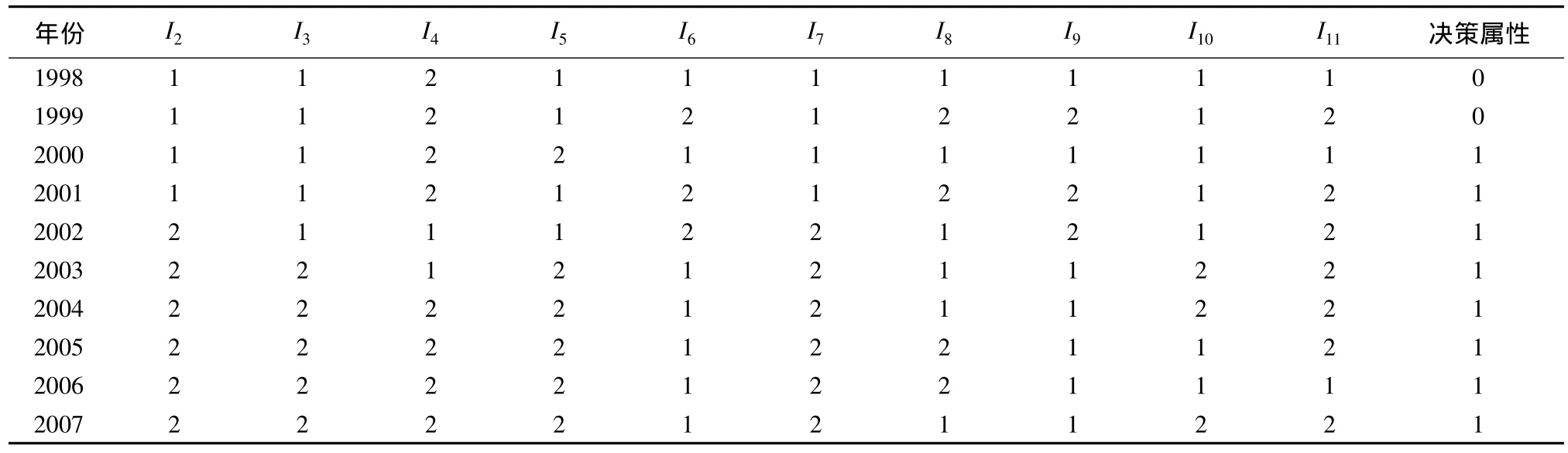
表3 各指標離散后數據類別及決策屬性

采用K-均值聚類的方法將表1中的樣本數據離散化，將各屬性下的列數據離散為兩類數據，分別用數字“1”和“2”來表示所分的類別。離散后的數據如表3所示，對應各個聚類中心I1(9.06，14.08)，I2(0.75，0.54)，I3(614，372)，I4(145.5，82.25)，I5(3438.75，2692.50)，I6(89.92，171.19)，I7(0.86，0.75)，I8(0.23，0.28)，I9(300.93，177.19)，I10(7.33，18.58)，I11(33.06，24.46)。

得到表3的離散數據后，對上述11個水資源危機識別因子進行屬性約簡，最終得到只含有3個識別因子的15條約簡，在此約簡基礎之上產生了83條相應的決策規則，通過從用戶主觀和系統客觀兩層面來衡量這些規則的價值，篩選出其中的約簡(萬元產值工業耗水量I4、農田灌溉用水定額I5、人均占有水資源量I9)作為水資源危機的預警指標，并通過對應的決策規則(表4)來進行預警。即通過{I4，I5，I9}這3個因子對應的數據就可以判斷水資源系統是否處于危機狀態，通過計算實際數據與聚類中心的距離，判斷樣本數據所屬類別后就可以按表4的規則知識來對水資源系統危機進行識別，快速而方便。

用BP神經網絡模型滾動預測預警指標2008—2012年的值，BP神經網絡的輸入層、隱層、和輸出層的神經元節點數分別為3、8、3，訓練網絡達到收斂后進行滾動預測，結果如表5所示。計算各預測值與 I4，I5，I9聚類中心的距離可知，2008—2012年滿足規則3:

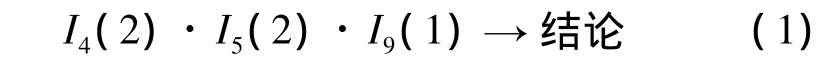
因此未來幾年內水資源系統不會發生突變，即不會產生危機。

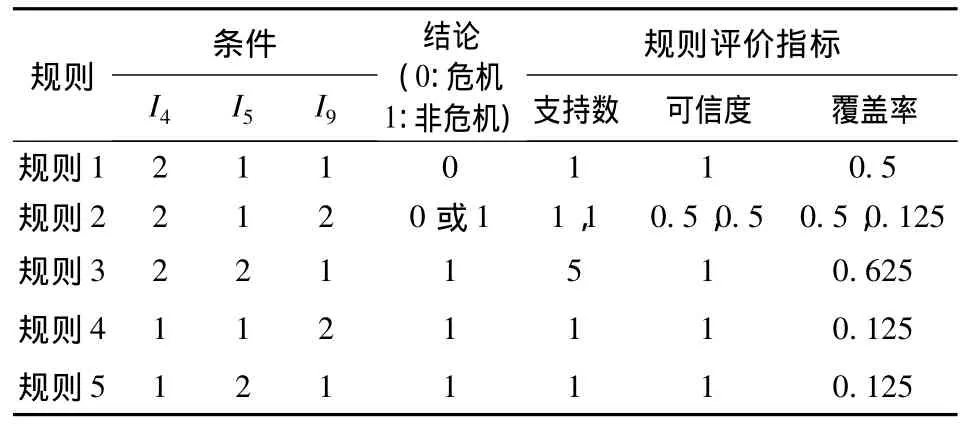
表4 水資源危機預警規則

3 結語

針對水資源系統具有突跳性、多徑性、發散性和可恢復性的特點，用尖點突變模型進行水資源危機識別，其中尖點突變模型中的正則因子和剖分因子分別通過對相應水資源危機識別因子進行主成分分析得到，將識別因子和識別結果分別作為決策表的條件屬性和決策屬性;針對粗糙集易于處理離散數據的特點，采用具有動態聚類特性和一定的自適應性的K-均值聚類算法對連續的識別因子數據進行離散化，對離散化的決策表進行屬性約簡確定出水資源危機預警指標和決策規則;針對預警指標間非線性關系復雜的特點，用BP神經網絡模型滾動預測預警指標，按照決策規則就可進行水資源危機預警判別。通過上述方法的耦合，建立了水資源危機預警的CC-RS-BP模型。

表5 用BP神經網絡預測各預警指標值

CC-RS-BP模型對A市進行水資源危機預警結果表明:分歧集Δ＜0的是1998和1999年，水資源系統處于不穩定狀態，將會發生突跳，即水資源系統處于危機狀態，其他年份Δ＞0，水資源系統處于穩定狀態，發生漸變;I4、I5、I9可以作為該地區的水資源危機預警指標，從系統客觀和用戶主觀兩層面在產生的83條規則知識中篩選出5條規則作為水資源危機預警的判別規則;BP神經網絡滾動預測2008—2012年的指標滿足其中規則3:

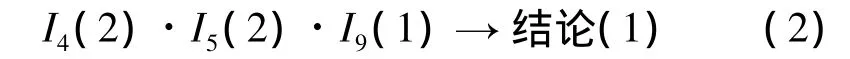
即未來幾年內水資源系統不會發生突變，這與A市2008—2010年的實際情況相吻合。

CC-RS-BP模型將尖點突變模型應用于內部作用尚未知的水資源系統，充分發揮了尖點突變理論直接處理不連續性而不聯系任何特殊的內在機制的優點，該模型的預警是以規則的形式來判斷的有別于傳統的預警方法，易被人理解和利用，模型采用BP神經網絡滾動預測預警指標值可以充分利用相鄰時期各指標的變化趨勢信息，為非線性、自學習、自適應、大規模并行分布多指標預測問題提供新途徑。

[1]周玉璽，馬傳棟.制度、技術、政策與水資源危機[J].中國生態農業學報，2006，14(2):1-4.

[2]劉梅.區域水資源危機的識別與對策研究[D].保定:河北農業大學，2009.

[3]陳紹金.水安全系統評價、預警與調控研究[M].北京:中國水利水電出版社，2006.

[4]文俊，李靖，金菊良.基于熵組合權重的區域水資源可持續利用預警模型[J].水電能源科學，2006，24(3):6-10.

[5]李仰斌，暢明琦.水資源安全評價與預警研究[J].中國農村水利水電，2009(1):1-4.

[6]申海亮.天津市水資源安全預警系統研究[D].天津:天津大學，2007.

[7]艾德春.我國煤炭供需平衡的預測預警研究[D].徐州:中國礦業大學，2008.

[8]徐襲，祝力，范學鑫.基于粗糙集與K-均值聚類的故障知識挖掘[J].微計算機信息，2007(15):141-142.

[9]呂光輝.中國西部干旱區生態安全評價、預警與調控研究:以新疆地區為例[D].烏魯木齊:新疆大學，2005.

[10]劉菁菁，田銀華.基于主成分-粗糙集理論的企業信貸風險預警研究[J].哈爾濱商業大學學報:社會科學版，2009(2):57-61.

[11]李升.地下水環境健康預警研究:以黃河下游懸河段(河南)為例[D].長春:吉林大學，2008.