基于HHT算法的軌道信號解調研究

楊菲菲，杜普選

（北京交通大學 國家電工電子教學基地， 北京 100044）

目前，軌道信號主要使用FFT（Fast Fourier Transform）和ZFFT（Zoom-FFT）結合的方法得到信號的調制頻率、上下邊頻，這些方法不能同時從時域和頻域2方面對信號進行分析，信號的上下邊頻不能從頻譜圖上直接觀察到。為此，本文采用一種新的時間序列信號分析方法解調軌道信號，即希爾伯特-黃變換（Hilbert-Huang Transform，HHT）算法。

1 ZPW2000軌道信號模型

ZPW2000軌道信號的低頻和載頻采用頻偏為11 Hz的UM71技術。該信號的頻譜特征是載頻附近的能量最大，上下邊頻附近的能量次之。信號載頻有4種并且每種又分為1型和2型，4種載頻分別為上行2 000 Hz、2 600 Hz，下行1 700 Hz、2 300 Hz。低頻調制信號共18種，以1.1 Hz的頻率從10.3 Hz～29 Hz遞增[1]。

采用相位連續(xù)的FSK信號的ZPW2000軌道信號，其時域表達式為[2～4]：

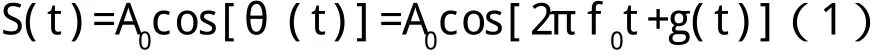
其中：

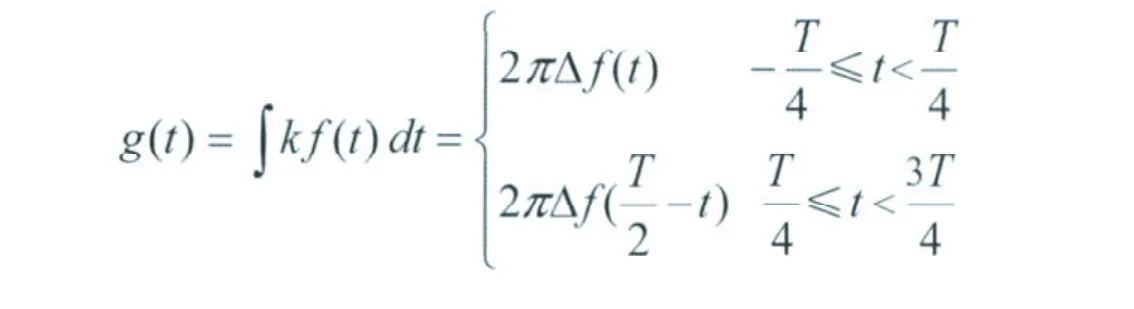
軌道信號的解調就是通過某種算法得到該鍵控移頻信號的載頻f0，調制頻率f1=1/T，上邊頻Fh=f0+△f，下邊頻Fl=f0－△f。

2 HHT原理

HHT由經典模態(tài)分解（Empirical Mode Decompo-sition，簡稱EMD）和Hilbert譜分析構成。HHT算法就是用EMD方法按照信號含有的信息量的不同，逐級分解成一系列的本征模態(tài)函數(shù)（Intrinsic Mode Function，IMF），然后求得每個IMF分量的解析函數(shù)，由解析函數(shù)求得其瞬時頻率和振幅[5]。

在HHT算法中，瞬時頻率的表達式為：

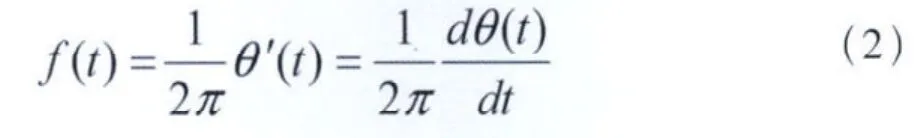
EMD通過自動調節(jié)時間尺度得到滿足要求的IMF函數(shù)。IMF函數(shù)滿足的性質為：（1）函數(shù)中所有的過零點的個數(shù)和極值點的個數(shù)之差的絕對值≤1；（2）在整個序列中，分別由信號的局部極大值和局部極小值形成的上下包絡的平均值處處為零或幾近于零。

EMD的篩選過程如下：首先分別求出原始信號y(t)的極大值和極小值點的上下包絡線，用y(t)減去上下包絡線的均值得到第一個殘余函數(shù)，如果該殘余函數(shù)滿足IMF函數(shù)的條件，則記為第一個IMF分量c1(t)。如果不滿足條件，則把該殘余函數(shù)視為一個新的信號重復上面的操作，直到找到符合IMF函數(shù)條件的殘余函數(shù)，把這個殘余函數(shù)記為第一個IMF分量，然后用y(t)減去c1(t)得到一個新的信號，重復上面的操作，得到其他IMF分量。分解停止的條件是直到找到的殘余函數(shù)是一個單純的遞增或遞減函數(shù)。得到EMD的最后分解式為[6]：

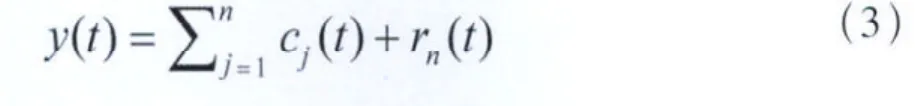
其中rn(t)為殘余函數(shù)，cj(t)為IMF分量。

3 用HHT算法對ZPW2000軌道信號解調

不同于以往用EMD分解和FFT算法結合的方法解調軌道信號，本文通過EMD分解得到正交的IMF分量，同時應用其瞬時頻率較為精確地解調出軌道信號的有用信息。

在實際環(huán)境中，鐵路信號不是純粹的FSK信號，所以在對信號的分析中加入了頻率為1 950 Hz和2 050 Hz的正弦噪聲。本文以載頻2 000 Hz、調制頻率22.4 Hz、頻偏11 Hz、信噪比為5 dB的軌道信號為代表進行分析。具體分析步驟如下：

（1）采用頻域濾波法對加入的正弦噪聲信號進行濾波。

（2）信號的EMD分解。求出濾波后的信號y1(t)的所有極值點（極大值點和極小值點），用3次樣條插值法進行曲線擬合，構造信號的上下包絡，求出兩者的均值m0(t)。用信號y1(t)減去m0(t)均值得到h1(t)，判斷h1(t)是否滿足IMF的2個性質，如果不滿足，則把h1(t)視為新的信號，重復上面的操作，直到找到滿足IMF條件的信號hk(t)，令c1(t)=hk(t)，得到第一個IMF分量，和殘余信號r1(t)=y1(t)－c1(t)。對殘余信號繼續(xù)進行EMD分解，直到殘余分量為常量或者是單調函數(shù)。這樣就得到了全部的IMF分量。

（3）求IMF分量的解析函數(shù)，并得到其瞬時頻率（簡稱IF）。

（4）求出上下邊頻和載頻。由瞬時頻率圖可以看出上下邊頻以某個值上下波動，為了求出準確的值，對瞬時頻率做一些數(shù)據上的處理。首先求出瞬時頻率IF在規(guī)定的時間窗口上的平均值f，以均值f作為中心把IF分為2個部分，即所有大于f的頻率為一部分，所有小于f的頻率為另一部分；對這2部分分別設置一個合適的范圍，求出該范圍以內的所有數(shù)據的平均值，所得的均值就是上邊頻fh和下邊頻fl；載頻f0=(fh+fl)/2。

（5）求調制頻率。由于從瞬時頻率圖形中不能直接求出調制頻率，所以本文對瞬時頻率做歸一化處理。即對頻率大于均值f的頻率置為1，對頻率小于均值f的頻率置為0，從而構成了一個方波信號。找到該方波中每個上升沿對應的位置，記為ki(i=1,2,…），則調制頻率為1/[(ki－ki－1)●△t]，使用8 192 Hz的采樣頻率，所以采樣周期△t為1/8 192 s，為得到精確的結果，對得到的所有調制頻率求平均值，得出最后的調制頻率。

4 Matlab仿真結果分析

載頻為2 000 Hz、調制頻率為22.4 Hz、頻偏為11 Hz、 信噪比為5 dB的軌道信號，經EMD分解得到10個IMF分量，如圖1。可知當分解到第10個IMF分量時，分量值基本接近于0，所以分解完畢。

圖1 EMD算法分解出的IMF分量

為了簡化計算量，有些IMF分量所含的信息量很少可以舍去。本文通過對IMF分量的頻譜與原始信號的頻譜作對比，找到和原始信號頻譜幾乎相同的IMF頻譜，如圖2。圖2中（1）、（2）、（3）分別是第1個IMF分量的頻譜、第2個IMF分量的頻譜、原始信號的頻譜。通過圖可知第1個IMF分量幾乎和原始信號相同，這樣只需取第1個IMF分量作為研究對象即可，可以減少運算量，加快解調的速度。

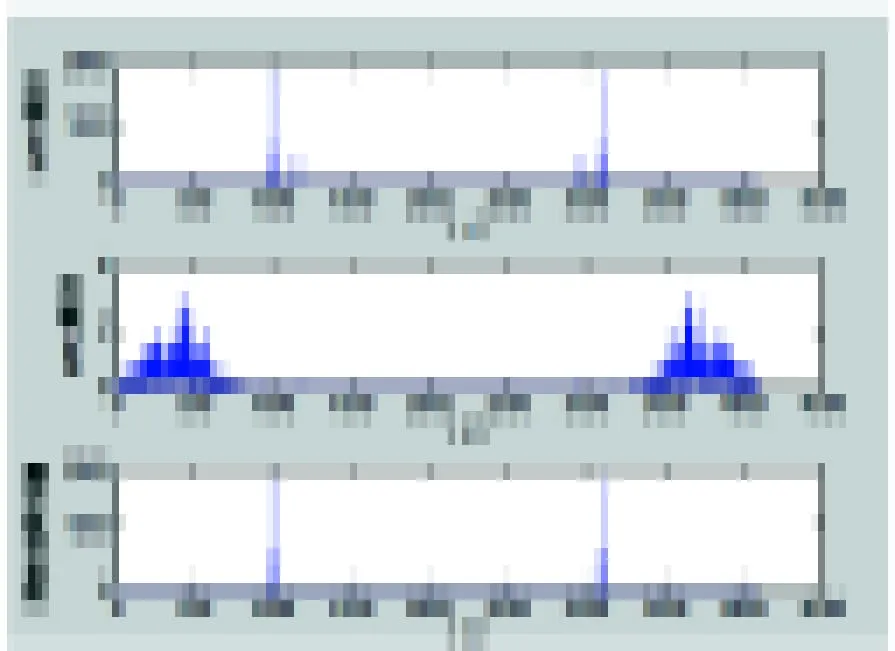
圖2 前2個IMF分量的頻譜與原始信號的頻譜對比圖

求得的第1個IMF分量的頻譜，如圖3，由圖可知，該信號的中心頻率在2 000 Hz，上邊頻以2 011 Hz為中心震動，下邊頻以1 989 Hz為中心震動。采用上述介紹方法可求出實際的上邊頻為2 010.948 4 Hz，下邊頻為1 988.852 1 Hz，中心載頻為1 999.867 1 Hz。誤差在0.15 Hz以內，達到軌道信號解調精度的要求。為了得到精確的調制頻率，采用歸一化處理，并對信號多個周期的調制頻率求平均值，如圖4。最后得到的調制頻率為22.400 9 Hz，誤差為0.000 9 Hz，解調結果非常理想。

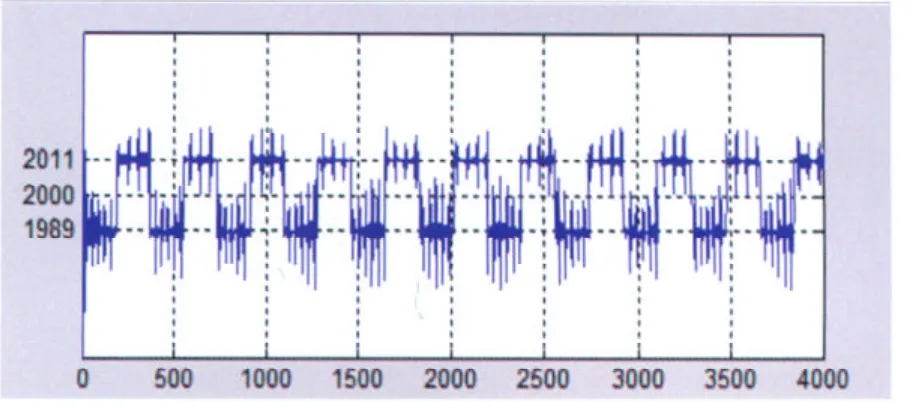
圖3 第1個IMF分量的瞬時頻率

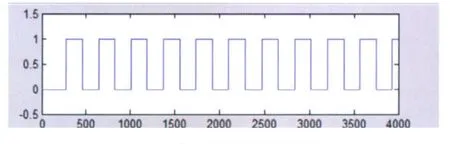
圖4 第1個IMF瞬時頻率歸一化

通過對ZPW2000軌道信號其他載頻的解調仿真，得到的解調結果和載頻為2 000Hz的解調結果具有相似的精度，調制頻率的解調結果比以往的解調精度高出很多，可見用HHT算法解調軌道信號是行之有效的。

5 結束語

本文采用HHT算法解調軌道信號，用HHT算法的核心經典模態(tài)分解法（EMD）得到本征模態(tài)函數(shù)（IMF），并求得瞬時頻率，通過瞬時頻率并結合信號的歸一化處理，實現(xiàn)了在信噪比較低的情況下對軌道信號的精確解調。與已有算法比較，本算法簡單，解調精確，可以直觀地得到信號的上下邊頻。

[1]林瑜筠，李 鵬. 鐵路信號新技術概論[M]. 北京：中國鐵道出版社，2007.

[2]柳艷紅，馬瑞軍，魏學業(yè). EMD算法在移頻信號解調中的應用研究[J]. 電子測量與儀器學報，2006，20（5）：34-38.

[3]周明晰，盧 迪，劉曉輝. 基于EMD和ZFFT的UM71軌道信號解調算法研究[J]. 自動化技術與應用，2008，27（9）.

[4]王雪麗. 基于TMS320C6720的軌道信號解調方案研究[J].北京交通大學，2010.

[5]N.E.huang, Z.Shen, S.R.Long, etai. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proc.R.Soc.Lond.A, l998.