遺傳算法在樹枝型專用線取送車作業中的應用研究
潘東亮
(神華包神鐵路有限責任公司 科技信息部,包頭 014014)
專用線取送車作業是鐵路貨運站的一項重要工作內容。合理地安排取送車順序,有利于加速車輛的周轉,縮短車輛的非生產停留時間,從而有效地提高鐵路貨物運輸的效率。對于求解樹枝型專用線取送車優化問題,提出了很多方法,也取得了一定的成果,其中遺傳算法的貢獻尤為顯著。遺傳算法(Genetic Algorithm-GA)是借鑒生物界自然選擇和自然遺傳機制的隨機搜索算法。遺傳算法作為一種搜索算法有著無可比擬的優點,表現在魯棒性強、全局搜索、并行性和高效性。
(1)文獻[1]和文獻[2]將取送車作業問題轉化成旅行商問題,以調車機車行走時間最短為優化目標,采用固定的交叉概率和變異概率,降低了搜索到問題最優解的效率;
(2)文獻[3]和文獻[4]利用哈密爾頓圖求解樹枝型專用線取送問題,該方法簡單直觀,但是當問題的規模較大時,卻難以找到最優解;
(3)文獻[5]以調車機車在整個取送作業中總耗時最少為最優目標,提高了鐵路貨物運輸的效率,但是只求得了送車順序,沒有求得取車順序,當以調車機車在整個取送車作業中總耗時最少為最優目標時,取車順序不是簡單地由送車順序決定的,取車順序與裝卸車時間有很大的關系。
上述文獻都將取車作業和送車作業分離開,沒有把它們看成是一個完整的作業,這樣不利于合理地安排取送車計劃。結合以上文獻的成果,對樹枝型專用線取送車問題進行了更深一步的研究,將取送車作業看成是一個完整的作業,不但得到送車順序,而且得到取車順序,同時建立了以調車機車在整個取送車作業中總耗時最少為最優目標的數學模型。采用改進的遺傳算法求解該問題,能夠得到合理的取送車順序,從而得到問題的最優解或近似最優解。
1 樹枝型專用線取送車問題的描述
1.1 樹枝型專用線取送車的特點
樹枝型專用線取送車作業的特點是:調車機車向某一專用線送取車完成之后不必返回車站,就能去其他專用線送取車,各專用線車輛的入線時刻不同,取回站內的時刻相同。本文討論的樹枝型專用線如圖1。
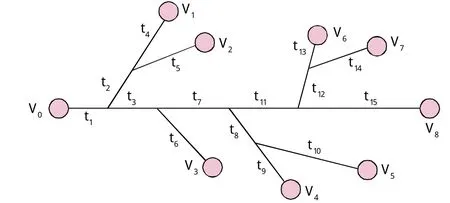
圖1 樹枝型專用線布置示意圖
圖1中V0代表調車機車的出發點和終點,Vi(i=1, 2,……, 8)代表各專用線的作業地點,ti(i=1, 2, ……, 15)代表調車機車在各路段的行走時間,這是已知的條件。由于現實中的取送車作業還受人為、天氣等眾多因素所影響,為了便于問題的討論,還需做如下假設:
(1)送往各專用線車輛的作業時間是已知的,其他輔助作業時間忽略不計;(2)有且僅有一輛調車機車負責一次取送車作業。
1.2 樹枝型專用線取送車數學模型
數學模型建立的好壞直接影響到是否能正確地搜索到問題的最優解。本文追求的最優目標是調車機車在一次作業中耗時最少,將取送作業看成是一次完整的作業,所以調車機車在一次作業中的耗時由送取車時間和等待完成作業時間決定,由此得到樹枝型專用線取送車數學模型:

其中,tij代表調車機車從專用線i到專用線j的行走時間(i=0, 1, 2,……, n;j=0,1, 2,……, n;n代表專用線),由于調車機車從站內出發,最后回到站內,所以一共有2n+1項tij,這樣就能保證把送往各專用線的車輛都能取回;tn'代表等待作業完成時間。設tn代表調車機車第2次到達專用線n與第1次到達專用線n的時間差,tn''代表調車機車第2次到達專用線n用的時間,tn'代表調車機車第1次到達專用線n用的時間,Tn代表專用線n的作業時間,則有如下關系:

如果Tn>tn,則調車機車取回專用線n的車輛時,等待作業完成時間公式如下:

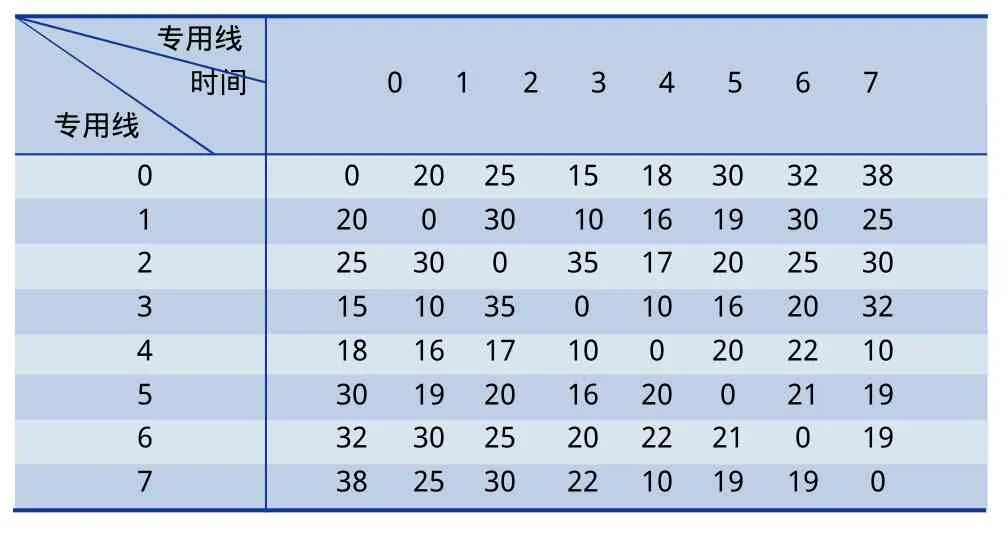
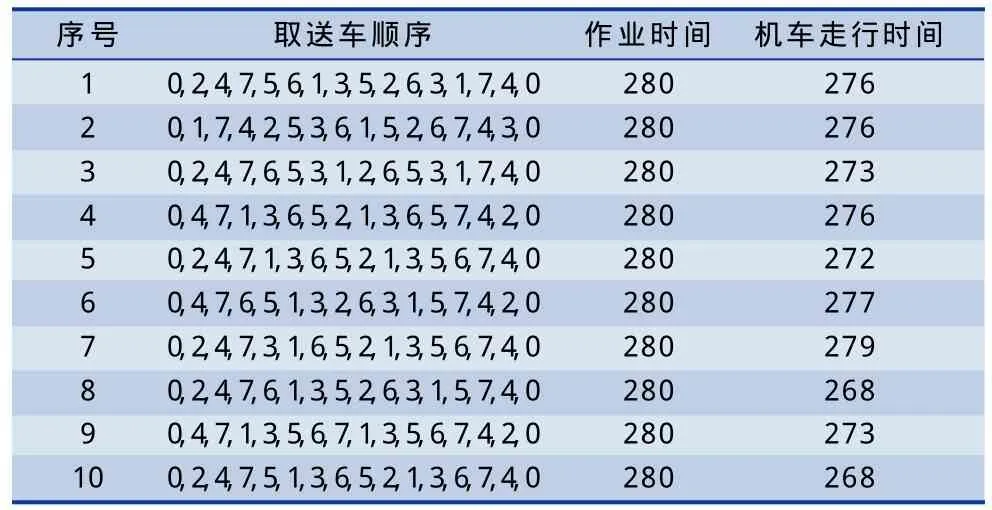
如果Tn 用(0,a1, a2,……, an-1,an, a1, a2,……, an-1, an,0)表示一條染色體,基因ai(i=1, 2, ……, n)為[1, n]之間互不重復的自然數,代表專用線。例如:染色體(0, 1, 2, 3, 2, 3, 1, 0),第1個0代表調車機車從站內出發開始作業,第2個0代表調車機車完成作業回到站內;第1個1代表調車機車將車輛送到專用線1,第2個1代表調車機車將車輛從專用線1取回,那么這條染色體的送車順序就是1、2、3,取車順序是2、3、1。 由于遺傳算法的初始種群隨機產生,優良染色體較少,極大地降低了算法的搜索效率。為提高算法的搜索效率,算法按照以下步驟生成染色體。 (1)送車時將作業量大的專用線盡量排在前面,作業量小的專用線排在后面;取車時將作業量小的專用線盡量排在前面,作業量大的專用線排在后面,減少調車機車的等待時間。 (2)設種群規模為M,則產生2 M個染色體,計算每條染色體的適應度,按照適應度大小將2 M個染色體進行排序,保留前M個染色體作為初始種群,淘汰后M個染色體。 在遺傳算法中,用適應度來確定某個體能進行遺傳操作的概率。適應度較大的個體遺傳到下一代的概率大,而適應度較小的個體遺傳到下一代的概率就小。度量個體適應度的函數稱為適應度函數。本文求解的最優目標是調車機車在一次作業中耗時最少,所以適應度函數f(x)為: 2.3.1 選擇運算 選擇運算采用精英比例選擇。記憶當前最優的個體,用它來替換本代群體經過交叉、變異后適應度最低的個體,對其他群體進行比例選擇運算。這種選擇運算的優勢是個體適應度大小與個體被選擇的概率成正比,利于種群的優化,能保證搜索到問題的最優解。 2.3.2 交叉運算 交叉運算采用兩點交叉。在(1,染色體長度-2)之間隨機產生兩個交叉點,交換待交叉兩條染色體兩個交叉點之間的基因,得到兩條新的染色體。判斷新的染色體是否合法,如果合法進入后續的運算;不合法將兩條新的染色體調整成合法的染色體,進入后續的運算。本文采用自適應的交叉概率。設f為某條染色體的適應度,favg為種群的平均適應度,隨機產生(0,1)之間的小數r1,(0.5, 1.0)之間的小數r2。 (1)當f≥favg,r1 (2)當f 染色體采用自然數編碼,交叉運算容易產生非法染色體,但是交叉運算能產生很多新的染色體,極大地維護了種群的多樣性,為更新種群、搜索到最優解做出了巨大貢獻。設待交叉的兩條染色體為A、B,交叉后的染色體為A'、B',交叉點為3和6,交叉結果如下: A'(0,1,3,4,5,2,1,4,5,2,3,0)B'(0,3,1,2,5,4,1,3,5,2,4,0) A(0,1,3,2,5,4,1,4,5,2,3,0)B(0,3,1,4,5,2,1,3,5,2,4,0) 2.3.3 變異運算 變異運算采用基本位變異。本文采用固定的變異概率。如果是取送結合的作業方式,在(1,染色體長度-2)之間隨機產生兩個變異點,交換兩點的基因。設待變異的染色體為A,變異后的染色體為A',變異點為2和6,變異結果如下: 如果是取送分離的作業方式,則隨機產生(0,1)之間的小數r1,當r1≥0.5時,兩個變異點在(1,染色體長度/2-1)之間產生;當r1<0.5時,兩個變異點在(染色體長度/2,染色體長度-2)之間產生,然后按照取送結合的變異方式進行變異。 按照改進的遺傳算法,可以解決樹枝型專用線取送車優化問題,算法流程圖如圖2。 圖2 算法流程圖 假設某車站銜接樹枝型專用線7條,且該站僅有一臺調車機車擔當取送車作業。現有一批列車組要送往各專用線進行作業,各專用線作業完成之后,調車機車要將列車取回,同時回到出發點。已知調車機車到各專用線的走行時間,如表1所示。各專用線的作業時間如表2所示。 表1 調車機車到各專用線的走行時間 表2 專用線作業時間 利用遺傳算法和本文提出的改進遺傳算法分別求解樹枝型專用線取送車優化問題,要求確定合理的取送車順序,使得調車機車在一次完整的作業中(包括取和送)耗時最少。設種群規模為50,進化代數為100,改進的遺傳算法采用本文提出的自適應交叉概率,遺傳算法的交叉概率為0.8,變異概率都為0.02,對取送車分離的作業方式分別進行100次實驗,算法效果對比如表3所示。 表3 兩種算法對比圖 由表3可以看出改進的遺傳算法搜索效率和準確率明顯優于遺傳算法,驗證了改進算法的有效性。利用改進的遺傳算法求得調車機車在一次完整的作業中最少的耗時為280,同時得到多條最優取送車順序,記錄了其中的10條最優取送車順序,如表4所示,作業時間包括機車取送車走行時間和等待作業完成時間。 由表4可以看出,雖然10種不同的取送車計劃都能使調車機車在一次完整的作業中耗時最少,但是機車的走行時間卻不完全相同。如果不但追求調車機車在一次完整的作業中耗時最少,而且希望機車的走行時間最少,則可以選擇方案8和方案10;還可以根據專用線的具體情況選擇不同的方案,因此利用改進的遺傳算法求解樹枝型專用線取送車優化問題利于鐵路貨運站效率的提高。 表4 最優的取送車順序 本文結合樹枝型鐵路專用線取送車的作業特點,建立了取送結合的作業模型,而不同于以往研究者只單方面研究送車作業或者取車作業。取送結合的作業方式符合現代鐵路運輸的需求,同時有利于加速車輛的周轉,縮短了車輛的非生產停留時間。本文改進的遺傳算法提高初始種群的適應度,優良的個體在種群中被遺傳的概率大,不良的個體被遺傳的概率小,從而提高了算法的搜索效率。仿真實驗驗證了模型和算法的優越性。由此可見,利用改進的遺傳算法求解樹枝型專用線取送車優化問題有較大的潛力。 [1]雷友誠,涂祖耀.基于遺傳蟻群算法的樹枝型鐵路取送車問題優化[J].中南大學學報,2011,42(8):2356-2362. [2]楊運貴,王慈光.樹枝行鐵路專用線取送車問題的遺傳算法研究[J]. 計算機工程與應用,2008,44(12):210-211. [3]張 健,宋建業. 貨物作業車取送模型的優化[J]. 鐵道貨運,2008,26(10). [4]余少鶴,李夏苗. 貨物作業車取送模型及算法研究[J]. 鐵道運輸與經濟,2002,24(12):46-48. [5]王雅琳,李開峰. 遺傳算法在企業鐵路取送調車作業優化中的應用[J]. 系統工程,2007,25(3):94-99. [6]楊 浩. 鐵路運輸組織學[M]. 北京:中國鐵道出版社,2006:157-163. [7]周 明,孫樹棟. 遺傳算法原理及應用[M]. 北京:國防工業出版社,1998:11-24.2 改進的遺傳算法求解樹枝型專用線取送車問題
2.1 初始種群的生成
2.2 適應度函數
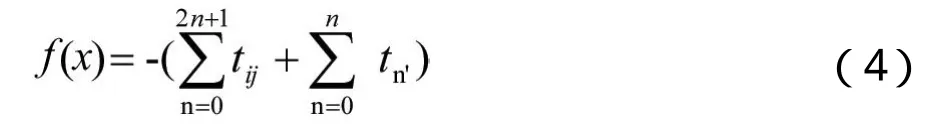
2.3 遺傳操作
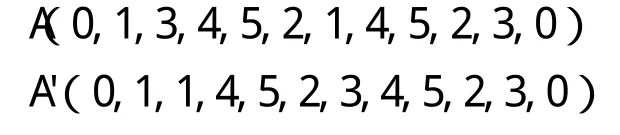
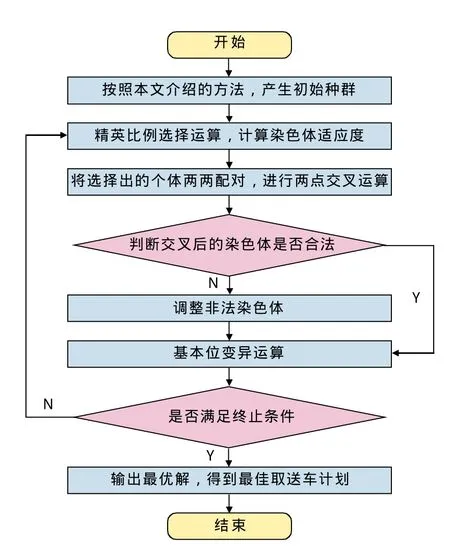
2.4 算法流程圖
3 仿真實驗與結果分析


4 結束語

