基于6σ穩健性方法的汽車行駛平順性優化

莫旭輝，趙宇航，鐘志華，張義

（湖南大學 汽車車身先進制造國家重點實驗室，湖南 長沙，410082）

汽車的平順性主要是保證汽車在行駛過程中產生的振動和沖擊環境對乘員舒適性的影響在一定界限之內[1]。在汽車各主要組成部分中，懸架是影響汽車行駛平順性最重要的因素，因此，懸架參數的設計及優化在整車研發中至關重要。近年來，為改善汽車行駛平順性，國內外學者做了大量的研究。趙旗等[2]建立了兩自由度汽車行駛平順性優化仿真模型，并運用遺傳算法對該模型進行了求解。Uys等[3]分析了某款越野車在不同路面上以不同速度行駛時的平順性，并通過改變懸架參數，優化其行駛平順性。然而，傳統的優化設計沒有考慮設計參數波動的影響，如懸架剛度和阻尼等的不確定性，這些設計變量的波動可能導致確定性優化結果失效。鑒于此，本研究建立整車 11自由度平順性模型，結合蒙特卡羅技術及6σ穩健優化設計方法，對整車行駛平順性進行穩健性優化，分析設計變量波動對優化結果的影響，通過對比結果，分析確定性優化與穩健性優化的優劣，并驗證穩健性優化設計方法在汽車平順性優化領域的工程實用性。

1 路面模型

我國的路面以B級和C級路面為主，考慮到研究對象的實際使用情況，選擇B級路面作為輸入。這里采用白噪聲濾波法構建路面信號[4]，其路面不平度表示如下：

式中：xi（t）為第i個車輪所受的路面不平度隨機激勵；f0為下截止頻率，f0=0.01 m?1；n0為參考空間頻率，n0=0.1 m?1；v為車速，v=20 m/s；Gq（n0）為路面不平度系數，在 B 級路面中，取 Gq（n0）=64×10?6m2/m?1；ω（t）為均值為0的白噪聲信號。

在 Matlab/Simulink環境中進行路面不平度的模擬，得到B級路面激勵時域仿真輸出結果如圖1所示。圖2所示為B級仿真路面與標準路面的功率譜密度，結果顯示：兩者的功率譜密度曲線重合度很高，所以，該B級仿真路面可以代替真實路面應用于仿真研究。

2 整車11自由度平順性仿真

圖1 B級路面時域模型Fig.1 B grade road in time domain

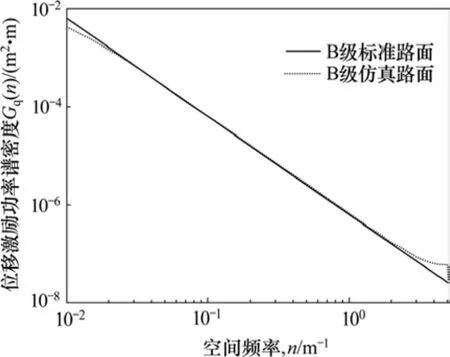
圖2 B級仿真路面與標準路面功率譜密度Fig.2 Power spectral density of B grade simulation road and standard road

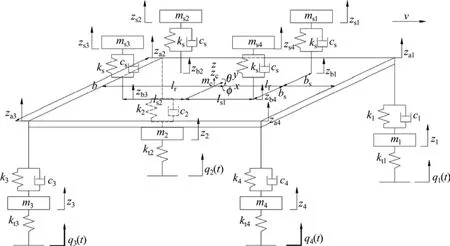
圖3 11自由度整車動力學模型Fig.3 Vehicle dynamics model with 11 DOFs

經過合理簡化，構建整車的11自由度整車動力學模型如圖3所示。所構建模型中，車身被視為剛體，有垂直振動、側傾轉動和俯仰轉動3個自由度，4個座椅和4個非簧載質量分別具有1個垂直振動自由度。整車坐標系以車身質心為原點O，以過原點向前的整車縱向對稱線為 X軸，以過原點垂直向上為 Z軸，Y=X×Z為右手坐標系。模型中各符號所代表的參數如表1所示。

表1 模型中的符號及代表的參數Table 1 Symbols and representatives in model

模型中各符號下標中出現的記號i=1,2,3,4，其代表的含義是：對于懸架和輪胎分別對應于左前、左后、右后和右前的位置；對于座椅則對應于駕駛員、左后乘客、右后乘客和副駕駛的位置。

基于牛頓定律可以建立 11自由度汽車平順性分析模型振動微分方程：式中：M為11×11階的質量矩陣；C為11×11階的阻尼矩陣；K為11×11階的剛度矩陣；Kt為11×1階的激勵矩陣，Z，分別為11×1階的位移、速度和加速度向量；Q為11×1階的激勵向量。

對于某款在研轎車，其有關參數如下：mc=1 200 kg；Ir=340 kg·m2；Ip=2230 kg·m2；m1=m4=40.5 kg；m2=m3=45.4 kg；ms=60 kg；kt1= kt2= kt3= kt4=190 kN/m；ks1=ks2=ks3=ks4=7 500 N/m；cs1=cs2=cs3=cs4=150 N·s/m；k1=k4=22 kN/m；k2=k3=24 kN/m；c1=c2=c3=c4=1 120 N·s/m；bl=br=0.74 m；lr=1.51 m；lf=1.25 m；ls=0.33 m；bs=0.54 m；v=20 m/s。

左前輪路面輸入采用式（1）中的路面模型。車輛在行駛時，同側前后車輪路面激勵相同，只是后輪比前輪滯后一段時間t0=（lr+lf）/v。由于車輛左右車輪所受路面激勵不同，考慮到路面的隨機性，右前輪和右后輪同樣采用式（1）中模型，但右前輪的路面激勵滯后任意時間t1（t1≠t0），右后輪滯后時間為t0+t1。

對11自由度整車動力學方程求解，得到各座椅垂向加速度均方根值，計算結果如表2所示。

表2 各座椅垂向加速度均方根值及加權振級Table 2 RMS values and weighted vibration levels of seats’vertical acceleration

根據文獻[5]中提到的加權振級和加權加速度與人的主觀感覺之間的關系，對于所研究的轎車，駕駛員和副駕駛感覺有一些不舒適，后排座椅的乘客感覺相當不舒適。

3 整車平順性優化

3.1 構建優化設計變量與約束函數

在表1所示的各個參數之中，輪胎剛度一般都經過標準化，不易改變，而座椅的參數受到制造上的制約，可選擇的余地不大，故選擇懸架剛度和阻尼作為設計變量[6?7]，而汽車的懸架一般是左右對稱的，即k1=k4，k2=k3，c1=c4，c2=c3。

對于所研究的車型，前懸架偏頻范圍為1.00～1.45 Hz，后懸架偏頻范圍為1.17～1.58 Hz。根據文獻[8]，結合已知參數，可以計算出懸架參數的取值范圍。

然而，考慮到制造和加工工藝，懸架的彈簧剛度和減振器阻尼容易受到制造過程和批量的影響，而它們的波動對整車的行駛平順性能有重要影響。由廠方提供的數據可知：阻尼制造誤差為±8%，懸架剛度的制造誤差為±11.3%[9]，設懸架剛度和阻尼均是服從以設計值為均值的正態分布的獨立變量，對應的標準差分別下式計算得到：

其中：σ為均方差；ε為誤差。最終確定優化變量如表3所示。

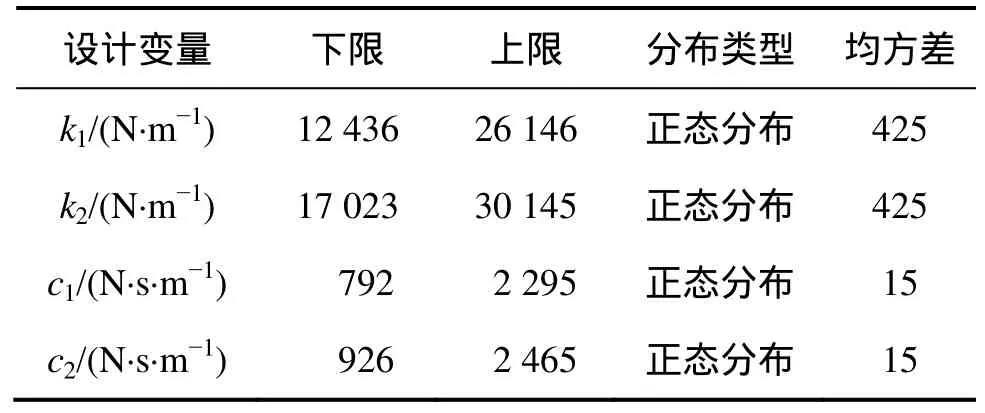
表3 設計變量Table 3 Design variables

為保證汽車正常行駛時，懸架的動撓度和車輪動載荷在適當的范圍內變化，車輪相對動載Fd/G和懸架的動撓度fd應滿足以下條件[8]：

式中：[fdi]為第i個懸架允許的最大動撓度，這里都取70 mm。

3.2 整車平順性的確定性優化

為保證汽車具有良好的行駛平順性，對于11自由度汽車模型，以各個座椅垂向加速度均方根azi最小為優化目標。結合以上的優化變量和約束條件，構建確定性優化模型如下：

3.3 基于蒙特卡羅模擬方法的整車平順性穩健性優化

穩健性是指在參數的不確定性影響下響應的穩定性。而穩健性優化則是在追尋目標函數最優解的同時，通過控制設計變量波動對優化目標的影響，達到降低目標函數在設計點上的敏感度及提高最優解的可靠性的目的。典型的穩健優化公式可以描述為[10]：

其中：C為約束值；x為設計變量；j為約束函數個數；xU和xL為設計變量的上、下限。

穩健性優化設計目標公式中的均值和方差可由蒙特卡羅模擬技術計算得到。進行蒙特卡羅計算，必須先對系統的仿真數值進行隨機抽樣[11]，將抽樣產生的隨機變量代入目標函數得到響應的蒙特卡羅云圖，并由蒙特卡羅云圖計算得到目標響應的均值和方差。

在式（4）中，約束可以改為質量約束，表示如下[12]：

其中：μ和σ分別為目標值的平均值和均方差；n為σ約束的質量水平，通過改變n以改變優化質量。在優化時，設計者由具體情況確定n，從而實現不同σ水平的優化。6σ穩健性優化設計則是將n設定為6，使約束及目標響應的優化結果均滿足6σ質量水平[13]。

工程設計中多目標穩健優化的數學模型為[14]：

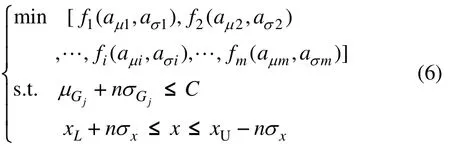
式中：C為約束值； fi（ aμi,aσi）為第 i個產品質量特性的穩健表達式；m為產品質量特性的個數。

根據優化分量的要求，合理構造穩健表達式，以各個座椅垂向加速度均方根最小為優化目標，共有 4個優化目標，均是最小特性的目標分量[15]。所以，構建整車平順性優化模型如下：

式中：λ為加權因子。

3.4 優化結果及分析

整車平順性的確定性優化和穩健性優化的設計變量優化結果如表4所示，在確定性優化中，整車懸架阻尼增大，剛度下降，并趨于下限值。而在穩健性優化中，整車懸架剛度和阻尼的變化趨勢雖與確定性優化的順序一致，但變化幅度較小。

表4 設計變量優化結果Table 4 Optimization results of design variables

初始方案、確定性優化和穩健性優化的各座椅垂向加速度均方根如表5所示，由表5可知：優化后各座椅的垂向加速度都有不同程度降低。這里以駕駛員座椅和其對應側的左前懸架與左前車輪為例進行分析。通過確定性優化，駕駛員座椅的垂向加速度均方根由0.403 6 m/s2降至0.293 7 m/s2，降低27.23%，均方差為0.035。而經過穩健性優化后，駕駛員座椅的垂向加速度均方根降至0.309 1 m/s2，降低23.41%，均方差為0.031。穩健優化在改善程度上雖然低于確定性優化的改善程度，但其優化結果的均方差較確定性優化減小11.43%，證明穩健優化結果更加穩定可靠。駕駛員座椅垂向加速度功率譜密度如圖4所示，由圖4可知：優化后，駕駛員的垂直加速度振動頻率主要集中 1～3 Hz，避開了人體的敏感振動頻率區域 4～12.5 Hz。

表5 各座椅垂向加速度均方根Table 5 RMS values of seats’ vertical acceleration

圖4 駕駛員座椅垂向加速度功率譜密度Fig.4 Vertical acceleration power spectral density for driver seat

各輪胎相對動載均方根如表6所示。由表6可知：經確定性優化，左前輪相對動載均方根由0.665 6升高至0.902 5，其σ水平為2.01，而經穩健性優化，左前輪相對動載均方根值升高至0.706 9，σ水平為6.15，σ質量水平得到大幅度提高。確定性優化與穩健性優化約束質量概率密度分布如圖5所示。確定性優化約束質量有部分超出邊界，而穩健性優化約束質量遠離邊界，證明其優化結果優于確定性優化結果。左前輪相對動載功率譜密度如圖6所示，由圖6可知：優化后，左前輪相對動載有一定幅度的增加，接地性變差。

表6 各輪胎相對動載均方根Table 6 RMS values of tires’ relative dynamic load

圖5 確定性優化與穩健性優化約束質量概率密度分布Fig.5 Constraint quality probability density distribution of deterministic optimization and robustness optimization

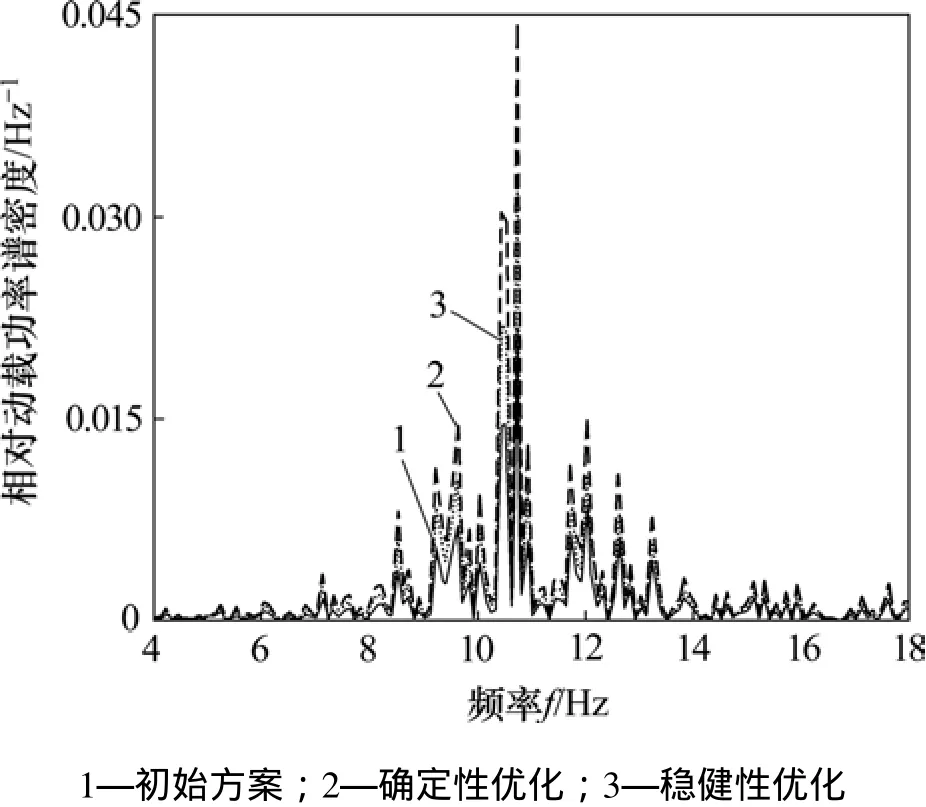
圖6 左前輪相對動載功率譜密度Fig.6 Relative dynamic load power spectral density for left front tire

左前懸架動撓度功率譜密度如圖7所示。由圖7可知：經確定性優化和穩健優化后，懸架動撓度相比優化前在整個頻域內均有所增加，但都在允許范圍內變化。同時，其σ水平均大于等于8，證明其具有較高的可靠性。綜合以上分析結果，經確定性優化和穩健性優化后的駕駛員座椅平順性均得到提高，但相比于確定性優化，穩健性優化的結果具有更強的抗干擾能力。

優化后，其他座椅的相關參數與駕駛員座椅也有類似的變化趨勢。

圖7 左前懸架動撓度功率譜密度Fig.7 Dynamic displacement power spectral density for left front suspension

4 結論

（1）建立了11自由度整車模型，結合蒙特卡羅抽樣技術和6σ穩健優化方法，在隨機路面輸入下，對其行駛平順性進行了優化。

（2）通過穩健性優化，一方面，整車行駛平順性得到顯著改善，另一方面，降低了優化結果對優化參數波動的敏感性，即使設計變量在最優解附近發生波動，也能保證整車行駛的平順性達到最優，即改善了優化目標的穩健性。

（3）穩健優化也大幅降低了因參數波動導致約束失效的概率，即提高了優化結果的可靠性。

（4）6σ穩健優化方法不僅為所研究的轎車確定了滿足平順性要求的懸架參數，為該轎車的設計與生產提供了理論依據，而且該方法也可以應用于懸架機構設計、汽車操縱穩定性優化及汽車平順性和操縱穩定性的協同優化等多個方面，具有廣闊的應用前景。

[1]余志生.汽車理論[M].5版.北京:機械工業出版社,2009:202?203.YU Zhi-sheng.Automobile theory[M].5th ed.Beiijng:China Machine Press,2009:202?203.

[2]趙旗,車華軍,李杰.基于遺傳算法的汽車行駛平順性優化仿真[J].機械設計與制造,2009（3）:203?205.ZHAO Qi,CHE Hua-jun,LI Jie.Automobile ride optimization simulation based on genetic algorithm[J].Machinery Design &Manufacture,2009（3）:203?205.

[3]Uys P E,Els P S,Thoresson M J.Suspension settings for optimal ride comfort of off-road vehicles travelling on roads with different roughness and speeds[J].Journal of Terramechanics,2007,44（2）:1163?1175.

[4]GB 7031—86,車輛振動輸入路面平度表示方法[S].GB 7031—86,Vehicle vibration-describing method for road surface irregularity[S].

[5]Dave C,喻凡.車輛動力學及其控制[M].北京:人民交通出版社,2003:72?73.Dave C,YU Fan.Vehicle dynamics and control[M].Beijing:China Communications Press,2003:72?73.

[6]Besselink I,van Asparen F.Numerical optimization of the linear dynamic behavior of commercial vehicles[J].Vehicle System Dynamics,1994,23（1）:53?70.

[7]Goncalves J P C,Ambrosio J A C.Road vehicle modeling requirements for optimization of ride and handling[J].Multi-body System Dynamics,2005,13（1）:3?23.

[8]劉惟信.汽車設計[M].北京:機械工業出版社,2002:181?182.LIU Wei-xin.Automobile design[M].Beijing:China Machine Press,2002:181?182.

[9]吳翹平.制造公差是影響螺旋彈簧剛度和彈力的主要因素[J].洪都科技,1996（4）:20?24.WU Qiao-ping.Influence of manufacturing tolerance as main factor spiral spring rigidity and tension[J].Hongdu Science and Technology,1996（4）:20?24.

[10]Koch P N,Yang R J,GU Lei.Design for six sigma through robust optimization[J].Structural and Multi-disciplinary Optimization,2004,26（3/4）:235?248.

[11]雷桂媛.關于蒙特克羅及擬蒙特卡羅方法的若干研究[D].杭州:浙江大學數學系,2003:17?18.WEI Gui-yuan.Study on the Monte Carlo and Quasi-Monte Carlo method[D].Hangzhou:Zhejiang University.Department of Mathematics,2003:17?18.

[12]李鐵柱,李光耀,陳濤,等.基于 Kriging近似模型的汽車乘員約束系統穩健性設計[J].機械工程學報.2010,46（22）:123?129.LI Tie-zhu,LI Guang-yao,CHEN Tao,et al.Robustness design of occupant restraint system based on Kriging Model[J].Journal of Mechanical Engineering,2010,46（22）:123?129.

[13]柳高潔,顧克秋.結合 NSGA-Ⅱ算法和蒙特卡羅模擬技術實現結構的魯棒優化[J].機械設計,2009,26（4）:65?67.LIU Gao-jie,GU Ke-qiu.Realizing the robust optimization of structures by combining the NSGA-Ⅱ algorithm with the Monte Carlo simulation technology[J].Journal of Machine Design,2009,26（4）:65?67.

[14]李玉強,崔振山,阮雪榆,等.6σ概率優化設計方法及其應用[J].中國機械工程,2004,15（21）:1916?1919.LI Yu-qiang,CUI Zhen-shan,YUAN Xue-yu,et al.6σ based probabilistic design optimization method and applications[J].China Mechanical Engineering,2004,15（21）:1916?1919.

[15]李玉強,崔振山,陳軍,等.基于響應面模型的 6σ穩健設計方法[J].上海交通大學學報.2006,40（2）:201?205.LI Yu-qiang,CUI Zhen-shan,CHEN Jun,et al.Six sigma robust design methodology based on response surface model[J].Journal of Shanghai Jiaotong University,2006,40（2）:201?205.