一種在無機晶體結構中檢索特定子結構的計算機方法

霍衛峰 李 乙,* 盧君然 于吉紅 徐如人 李 晶

(1吉林大學無機合成與制備化學國家重點實驗室,長春130012;2北京科技大學應用力學系,北京100083)

一種在無機晶體結構中檢索特定子結構的計算機方法

霍衛峰1李 乙1,*盧君然1于吉紅1徐如人1李 晶2

(1吉林大學無機合成與制備化學國家重點實驗室,長春130012;2北京科技大學應用力學系,北京100083)

提出了一種針對無機晶體化合物的子結構檢索方法.該方法以VF2子圖同構算法為基礎,針對無機晶體化合物的結構特點,采用了兩種策略以提高子結構檢索的效率:(1)引入晶體的對稱性信息避免了在等價原子間進行的大量重復性計算;(2)采用結構編碼預篩選可以有效地減少目標結構的數量.我們以在無機微孔分子篩數據庫中進行子結構檢索為例測試該方法的有效性.測試結果表明,該方法可以快速且準確地在分子篩數據庫中檢索包含特定子結構的記錄.兩種檢索策略的引入大大降低了子結構檢索的復雜度,檢索速度可提高3-5個數量級.該方法通過Perl語言實現,具有較好的可移植性.

無機晶體材料;數據庫;子結構檢索;VF2算法;分子篩;構筑基元

1 引言

分子結構檢索是利用計算機程序從數據庫中提取分子結構信息的過程,是化學信息學的核心研究領域之一,1其中的子結構檢索問題是研究最多的課題之一.簡單而言,子結構檢索就是利用計算機方法在分子結構數據庫中尋找包含特定子結構的分子.目前,子結構檢索主要應用于在有機分子結構中尋找特定的官能團,主要有ParMol、2MoFa、3FFSM、4gSpan、5Gaston、6SMSD7等方法.和有機分子一樣,無機晶體材料的子結構(構筑基元)對無機晶體材料的結構、性質以及合成研究至關重要,8,9因此針對無機晶體材料的子結構檢索同樣具有非常重要的意義.

然而,和以獨立分子為單位的有機晶體材料不同,無機晶體結構往往是三維方向無限延展的,沒有像有機分子一樣的特定獨立單元,數以萬計不同配位狀態的原子相互連接形成一個巨大的拓撲網絡結構.在如此巨大的體系中進行子結構檢索是一個非常復雜的問題;而當檢索范圍擴大到由大量復雜無機結構組成的數據庫時,子結構檢索將變得難以實現.目前在化學領域中使用最廣泛的晶體結構數據庫是劍橋結構數據庫(CSD),10數據庫中包含劍橋晶體數據中心開發的子結構檢索工具Conquest,11其原理和有機分子的檢索類似,即把龐大的晶體結構分割為有限大小的晶體學不對稱單元,進一步把這些不對稱單元當作獨立分子進行子結構檢索.這種檢索方法的局限性是顯而易見的:首先,無機晶體的不對稱單元在理論上是可以任意選取的,僅憑不對稱單元無法代表整個無機骨架結構;更為重要的是,當待檢索的子結構位于一個以上不對稱單元的交界時,像Conquest這種只檢索不對稱單元內部的方法是無法識別不對稱單元之間的關聯的.因此以晶體學不對稱單元或獨立分子為基礎的子結構檢索方法并不適用于不具備獨立單元的無機晶體結構.目前,對無機晶體結構進行子結構檢索的唯一途徑是將其骨架拓撲網絡擴展到相當大的范圍內(例如8個晶胞),而擴大的拓撲網絡同時會使計算量以指數形式遞增,當檢索的對象是包含大量無機結構的數據庫時,子結構檢索將變得難以實現.

由此可見,無機晶體材料子結構檢索的重要性和理論方法的局限性迫切要求新方法的誕生.基于這些問題,結合無機晶體材料的結構特點,我們提出了一種可以在無機晶體結構中有效地進行子結構檢索的方法.

2 方法

將無機晶體結構中的中心原子看作節點,將節點之間的連接看作邊,無機晶體結構就可以轉化成圖論中的圖,子結構檢索問題就轉化成為圖論中的子圖同構問題.子圖同構是非確定多項式時間完全問題(NPC),即沒有方法可以在合理的時間內(多項式時間)解決它.12算法的時間消耗是隨節點(中心原子)數的增加呈指數級增長的,可以想象,對于包含大量原子的無機晶體結構而言,傳統的子圖同構算法是難以實際應用的.

很多研究嘗試將子圖同構算法的復雜程度降至可以實際應用的程度,主要的算法包括Ullmann算法、13SD算法、14Nauty算法、15VF算法16和VF2算法17等.其中,VF2算法是在VF算法的基礎上發展起來的,和VF算法相比,VF2算法成功地將空間復雜度從O(N2)降到了O(N),其中N為圖中的節點數.特別是在規則圖(每個節點都具有相同數目鄰接節點的圖)和大圖(節點數大于600的圖)的同構計算中,VF2算法具有比其他算法更高的性能.1,18-21因為無機晶體的拓撲網絡結構絕大多數屬于規則圖和大圖,所以我們采用VF2子圖同構算法作為子結構檢索方法的基礎.

VF2算法是一種深度優先的回溯算法,算法的高效性得益于采用了狀態空間表示(SSR)的方法和減少搜索空間的一些匹配規則.16

圖1為檢索圖(Q)和目標圖(T)示意圖.如圖1所示,假設要查詢的圖Q中有N1個節點,目標圖T中有N2個節點,N1≤N2.M是Q和T之間的映射,包含點對(q,t),其中,q∈Q,t∈T,M?N1×N2.狀態空間S是M的一個子集,用于存儲圖Q和圖T的局部匹配.點對(qi,ti)是否可以加入S,取決于其是否滿足匹配規則.在這里,我們規定點對(qi,ti)加入S的規則是:(1)qi與ti的類型要一致;(2)對于S中任一已有的點對(qi-1,ti-1),如果qi與qi-1相連,則ti和ti-1必須相連;(3)ti的鄰接節點數要小于或等于qi的鄰接節點數.

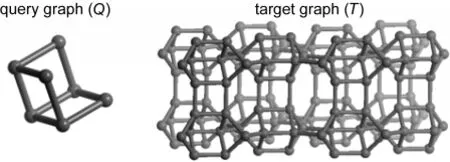
圖1 檢索圖(Q)和目標圖(T)示意圖Fig.1 Diagrams of query graph(Q)and target graph(T)

狀態空間S的初值S0為空.從查詢圖Q中選擇任意一個未訪問過的節點q1,在目標圖T中尋找當前這一輪未被訪問過的且滿足匹配規則的對應節點.如果Q中的第一個節點q1沒有在T中找到對應的節點,則Q不是T的子圖;如果能找到這樣的節點t1,就將點對(q1,t1)放入狀態空間S中,然后從節點q1在Q中的后繼節點集(與節點q相連的節點集合)中選擇一個節點q2,再從節點t1在T中的后繼節點集(與節點t1相連的節點集合)中尋找滿足匹配規則的對應節點.如果成功找到對應節點t2,則將點對(q2, t2)放入到狀態空間S中;如果找不到就回溯到上一輪,開始新的查找.當狀態空間S中有N1個點對時,表明圖Q是圖T的子圖,輸出結果.

因為無機晶體結構中包含的節點數是非常龐大的,直接采用VF2算法對無機晶體結構進行檢索仍然是不現實的.在此基礎上,根據無機晶體材料的結構特點,我們在VF2算法的基礎上做了兩個重要的改進以提高檢索效率.

(1)利用晶體結構的對稱性.在進行匹配前,分別將待檢子結構片段(查詢圖Q)和目標晶體結構片段(目標圖T)中的晶體學獨立或不對稱的原子(節點)移至相應圖的頂部.在進行子圖匹配時,檢驗Q中是否有與T中晶體學獨立節點相匹配的獨立節點,如果沒有找到滿足匹配規則的節點,就可以認為待檢結構不是目標結構的子結構,而并不需要遍歷待查詢的子結構及目標結構中的所有節點,從而大大提高計算的效率.

(2)采用編碼預篩選方法.由于子圖匹配算法的計算量非常大,因此如果在進行子圖匹配之前能夠預篩選掉大量確定無效的數據而僅保留少量有可能符合檢索條件的數據,將極大提高子結構檢索的效率.為此,我們設計了一個具有特定位數的二進制編碼,編碼中的每一位對應一種特定的構筑基元.以無機微孔分子篩晶體結構為例來說,我們采用了一個19位的二進制編碼,編碼中的每一位代表了19種在分子篩結構中最常見的構筑基元22(表1),編碼中每一位的值1或0代表該結構中含有或不含有指定的構筑基元.在進行子圖匹配計算之前,我們先通過計算機程序把待查詢的子結構和目標結構分別轉換成編碼(如圖2所示),然后對比編碼中相應位上的值,如果待查詢子結構編碼中的某一位顯示含有某個特定的構筑基元而目標結構編碼顯示不含有,說明待查詢子結構中包含目標結構中所不包含的構筑基元,因此可以直接判定目標結構不包含待查詢的子結構;如果待查詢的子結構中所有的構筑基元在目標結構編碼中都顯示含有,則說明目標結構有可能包含待查詢的子結構,需要進一步通過子圖匹配計算以確定兩者是否具有包含關系.對于僅包含少量目標結構的數據庫而言,編碼預篩選的優越性并不明顯.隨著數據庫中目標結構數量的增加,編碼預篩選的優越性將迅速顯現出來.需要強調的是,目標結構的編碼轉換是在子結構檢索之前完成并保存的,并不占用子圖匹配計算的時間.

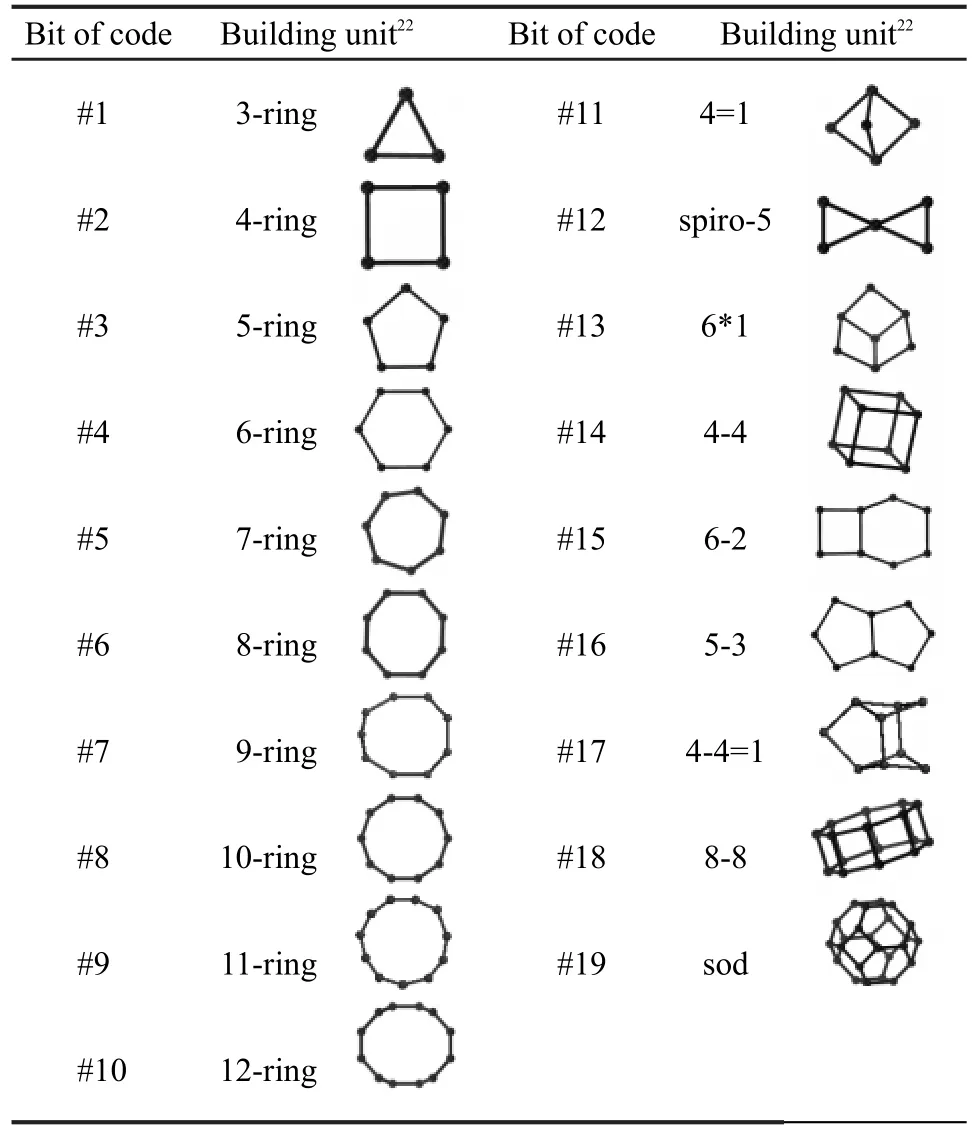
表1 19個分子篩結構編碼中各位所代表的構筑基元Table 1 Prescreening code for 19 zeolite structure building units

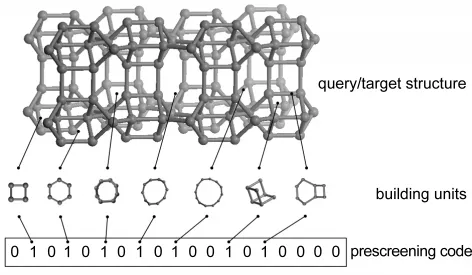
圖2 結構編碼Fig.2 Structure encoding

3 結果與討論

我們以在分子篩晶體結構中檢索特定的子結構為例測試這種方法的效率.數據源采用了國際分子篩協會(IZA)官方網站提供的197種分子篩結構的cif文件.22從每個結構的cif文件出發,計算了8個晶胞內容所對應的鄰接矩陣并合并在一起形成結構數據庫.選取了一些已知的分子篩構筑基元作為待查詢的子結構片段,在由197種分子篩晶體結構所組成的數據庫中進行檢索,并將檢索結果與分子篩協會官方網站提供的手工檢索結果相對比,以此檢驗我們這種檢索方法的準確性.在此基礎上,我們又任意定義了一些新的構筑基元,進一步考察這種結構檢索方法在不同條件下的效率.測試的硬件環境是Intel Core2 Duo T9600 2.8 GHz,4 GB DDR2 800 MHz,操作系統為Windows 7 Ultimate SP1 32位,程序開發環境為ActivePerl 5.12.4.

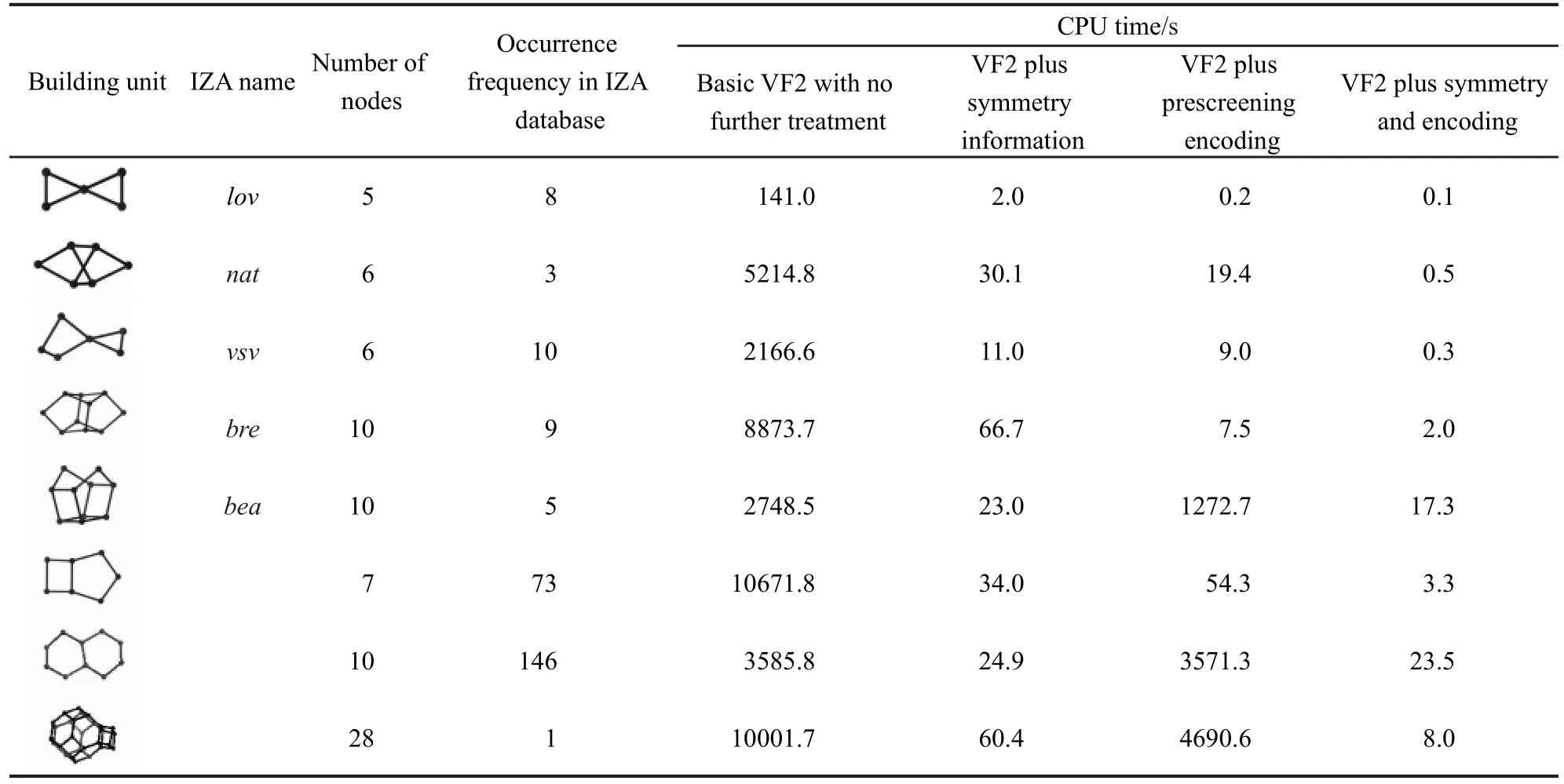
表2 采用不同策略進行子結構檢索所需時間的比較Table 2 Time needed for substructure search by different approaches

選取的已知分子篩構筑基元包括lov、nat、vsv、bre、bea等,22部分測試結果列在表2中.國際分子篩協會經過人工分析,在其官方數據庫中給出了這些常見的構筑基元在197個分子篩結構中出現的情況.經過對比發現,采用我們的子結構檢索方法得到的結果與國際分子篩協會人工統計的結果完全一致.說明我們的子結構檢索方法在準確性上是可靠的.

此外,表2還列出了各種檢索策略所需的CPU時間，包括單純的VF2檢索、引入對稱性的VF2檢索、采用編碼預篩選的VF2檢索以及同時引入對稱性和編碼預篩選的VF2檢索.盡管這四種策略所得到的檢索結果完全一致,但檢索效率卻相差較大.單純的VF2算法耗時非常長,在由197個結構組成的數據庫中進行子結構檢索一般需要1 h以上的CPU時間.而在引入了對稱性信息之后,檢索消耗的時間會降低2-3個數量級.從理論上說,對稱性的引入可以大大降低VF2算法所需遍歷的節點個數,因此VF2算法的效率會得到指數級的提升.此外,編碼預篩選能夠在子圖同構計算之前大幅度縮小目標結構的數量,同樣也可以大幅度提高結構檢索的效率.需要說明的是,待檢的結構片段越特殊、越少見,編碼預篩選提升的效率就越高,這個特性恰恰可以滿足實際需求.因為在實際應用中,人們往往對新穎少見的子結構更關心,更需要在數據庫中挖掘其結構特殊性.我們提出的采用編碼預篩選的子圖同構算法恰恰可以有效地解決這類問題.引入晶體結構對稱性和編碼預篩選這兩套方案分別基于不同的原理,因此將這兩種方法同時結合在一起,可以將子結構檢索的效率進一步提升.從表2的最終結果可以看出,同時采用這兩種改進方法的檢索策略是效率最高的,對于簡單的結構通常可以在1 s之內完成檢索;對于相對復雜的結構,檢索時間會略有增加,但仍在實際可接受的范圍內.

4 結論

提出了一種針對無機晶體材料的子結構檢索方法.該方法基于子圖同構的VF2算法,利用晶體結構的對稱性和編碼預篩選策略降低結構檢索的復雜度,可以在無機晶體數據庫中快速準確地檢索包含特定子結構的記錄,為無機晶體材料的結構分析提供了重要的研究工具.本文以分子篩結構為例展示了這種結構檢索方法的效率.除此之外,該方法同樣可以用于其他無機晶體結構的檢索,包括在假想分子篩結構數據庫、23多配位態的開放骨架結構數據庫、24甚至致密的礦物晶體結構數據庫中進行的子結構檢索.采用Perl語言實現了這種檢索方法,其高度的可移植性使得這種檢索方法可以在絕大多數計算機平臺上得以實現.

(1) Rijnbeek,M.;Steinbeck,C.J.Cheminf.2009,1,17.

(2) Worlein,M.Extension and Parallelization of a Graph-Mining-Algorithm.Ph.D.Dissertation, Friedrich-Alexander-Universit?t Erlangen-Nürnberg,Germany, 2006.

(3) Meinl,T.;Borgelt,C.;Berthold,M.R.Discriminative Closed Fragment Mining and Perfect Extensions in MoFa.In Frontiers in Artificial Intelligence and Applications;Onaindia,E.,Staab, S.Eds.;IOS Press:Amsterdam,2004;Vol.109,pp 3-14.

(4) Huan,J.;Wang,W.;Prins,J.Efficient Mining of Frequent Subgraphs in the Presence of Isomorphism.In Proceedings of the 3rd IEEE International Conference on Data Mining, Melbourne,FL,USA,Nov 19-22,2003;Wu,X.D.,Tuzhilin, A.,Shavlik,J.Eds.;IEEE Computer Soc.:LosAlamitos,CA, 2003.

(5)Yan,X.F.;Han,J.W.gSpan:Graph-Based Substructure Pattern Mining.In Proceedings of 2002 IEEE International Conference on Data Mining,Maebashi City,Japan,Dec 9-12,2002; Kumark,V.Ed.;IEEE Computer Soc.:LosAlamitos,CA,2002.

(6) Nijssen,S.;Kok,J.N.Electronic Notes in Theoretical Computer Science 2005,127(1),77.

(7) Rahman,S.A.;Bashton,M.;Holliday,G.L.;Schrader,R.; Thornton,J.M.J.Cheminf.2009,1,12.

(8) Sastre,G.;Vidal-Moya,J.A.;Blasco,T.;Rius,J.;Jordá,J.L.; Navarro,M.T.;Rey,F.;Corma,A.Angew.Chem.Int.Edit. 2002,41,4722.

(9) Corma,A.;Rey,F.;Valencia,S.;Jordá,J.L.;Rius,J.Nature Mater.2003,2,493.

(10) Cambridge Structure Database.http://www.ccdc.cam.ac.uk/ products/csd/(accessedAug 30,2011).

(11) Bruno,I.J.;Cole,J.C.;Edgington,P.R.;Kessler,M.K.; MacRae,C.F.;McCabe,P.;Pearson,J.;Taylor,R.Acta Crystallogr.B:Struct.Sci.2002,58,389.

(12) Cook,S.A.The Complexity of Theorem-Proving Procedures.In Proceedings of the Third Annual ACM Symposium on the Theory of Computing,Ohio,USA,May 3-5,1971;Harrison, M.A.,Banerji,R.B.,Ullman,J.D.Eds.;ACM:New York, 1971.

(13) Ullmann,J.R.J.Assoc.Comput.Mach.1976,23,31.

(14) Schmidt,D.C.;Druffel,L.E.J.Assoc.Comput.Mach.1976, 23,433.

(15) McKay,B.D.Congressus Numerantium 1981,30,45.

(16) Cordella,L.P.;Foggia,P.;Sansone,C.;Vento,M.Performance Evaluation of the VF Graph MatchingAlgorithm.In Proceedings of the 10th International Conference on Image Analysis and Processing,Venice,Italy,Sept 27-29,1999; Roberto,G.,Cantoni,V.,Levialdi,S.Eds.;IEEE Computer Society Press:LosAlamitos,1999.

(17) Cordella,L.P.;Foggia,P.;Sansone,C.;Vento,M.IEEE Transactions on Pattern Analysis and Machine Intelligence 2004,26(10),1367.

(18) Su,Z.Q.;Liao,C.Z.;Xie,A.H.;Lu,X.P.;Shi,L.M. Computers and Applied Chemistry 2003,20(5),556.[蘇振強,廖晨鐘,謝愛華,魯先平,石樂明.計算機與應用化學, 2003,20(5),556.]

(19) Li,X.;Song,T.T.;He,X.F.Computers and Applied Chemistry 2007,24(11),1551.[李 欣,宋婷婷,何險峰.計算機與應用化學,2007,24(11),1551.]

(20) Song,T.T.;He,X.F.;Wen,H.Computers and Applied Chemistry 2008,25(9),1152.[宋婷婷,何險峰,溫 浩.計算機與應用化學,2008,25(9),1152.]

(21) Feng,H.J.;Wang,Y.;Zhou,J.L.;Haji,A.Computer Applications and Software 2010,27(10),117. [馮紅君,汪 漪,周俊林,阿吉艾克拜爾·艾薩.計算機與應用軟件, 2010,27(10),117.]

(22) The Database of Zeolite Structures.http://www.iza-structure.org (accessedAug 30,2011).

(23) Li,Y.;Yu,J.H.;Xu,R.R.Hypothetical Zeolite Database.http:// mezeopor.jlu.edu.cn/hypo/(accessedAug 30,2011).

(24) Li,Y.;Yu,J.H.;Xu,R.R.AlPO Database.http://mezeopor.jlu. edu.cn/alpo/(accessedAug 30,2011).

November 17,2011;Revised:December 27,2011;Published on Web:January 4,2012.?

.Email:yili@jlu.edu.cn;Tel:+86-431-85168609.

A Computational Method for Specified Substructure Search in Inorganic Crystal Structures

HUO Wei-Feng1LI Yi1,*LU Jun-Ran1YU Ji-Hong1XU Ru-Ren1LI Jing2
(1State Key Laboratory of Inorganic Synthesis and Preparative Chemistry,Jilin University,Changchun 130012,P.R.China;2Department of Applied Mechanics,University of Science and Technology Beijing,Beijing 100083,P.R.China)

In this paper,a computational method for the substructure search in inorganic crystal structures is proposed.This method is based on the VF2 subgraph isomorphism algorithm.Furthermore, two additional approaches have been introduced into this method to improve the calculation efficiency of VF2:(1)introduction of crystal symmetry information with a view to avoiding redundant calculations among equivalent nodes(atoms);(2)a prescreening encoding treatment to enhance the calculation efficiency by greatly reducing the number of target structures.We tested the efficiency of this method by searching the zeolite crystal structure database from the International Zeolite Association for entries containing specified building units.The test results showed that this method could quickly and correctly retrieve all the entries containing the queried substructure in the zeolite structure database.The introduction of crystal symmetry information and the prescreening encoding treatment greatly reduce the complexity of substructure search. The search speed was significantly enhanced by at least 3-5 orders of magnitude.This method was developed using Perl programming language,ensuring that this method could be easily applied to various platforms.

Inorganic crystal structure;Database;Substructure search;VF2 algorithm;Zeolite; Building unit

10.3866/PKU.WHXB201201041

O641

The project was supported by the National Natural Science Foundation of China(21001049).

國家自然科學基金(21001049)資助項目