面內彈性繩系衛星系統的內共振?

夏 潔,龐兆君,金棟平

(南京航空航天大學振動工程研究所,機械強度與振動國家重點實驗室 ,江蘇 南京 210016)

引 言

繩系衛星作為一種新型空間技術具有巨大潛力,正日益受到學術和航天界的關注[1～5]。繩系衛星系統為高維非線性動力學系統,由于繩系衛星在工作狀態往往需要穩定的狀態保持,因此研究狀態保持階段繩系衛星的非線性行為具有重要意義。Nixon對于繩系衛星面內外動力學行為進行了解析和數值研究,給出了系統參數對于周期、概周期及混沌運動的影響[6]。 Fujii等研究了系繩彈性和軌道偏心率引起的繩系衛星狀態保持階段的分叉問題[7]。Misra等研究了狀態保持階段的面內非線性動力學[8]。此后,他們又考慮了面內外耦合的三維繩系衛星系統,結果表明圓軌道和橢圓軌道均存在混沌運動且混沌區隨Hamilton函數的增加而增大。Celletti和 Sidorenko等研究了“啞鈴”型繩系衛星系統在圓軌道及橢圓軌道上的姿態動力學。研究表明,圓軌道繩系衛星系統的局部平衡位置是穩定的,而橢圓軌道的平衡位置呈現出周期時變性[9]。此后,他們還研究了不計系繩質量時彈性連接的繩系衛星系統面內周期運動的分叉及其穩定性問題[10]。

當考慮系繩彈性時,由于系繩縱向和面內俯仰運動耦合,使得繩系衛星系統成為一復雜的含陀螺項的非線性動力學系統。在現有的研究中,人們大多集中于周期、概周期、混沌及其運動穩定性分析,而對繩系衛星系統運動耦合導致的非線性共振尚未有深入研究。本文針對一彈性繩系衛星系統的非線性耦合振動問題,應用多尺度方法研究了其在狀態保持階段的非線性共振,分析了可能的參數組合所導致的共振問題,獲得了基于 Jacobi橢圓函數的繩系衛星系統 2∶1內共振的解析解。

1 系統模型

研究“彈簧-質點”型面內繩系衛星系統。點質量分別為m1和m2的衛星通過質量為mt的一均質分布的彈簧相連,系統質心O1沿偏心率為e的未擾 Kepler橢圓軌道運動,考慮整個系統在軌道面內運動,如圖1所示。設彈簧僅發生沿其自身的縱向振動,只考慮重力梯度且重力場局部呈線性。建立固連于地心的慣性坐標系O-XY和固連于系統質心的軌道坐標系O1-xy。軌道坐標系單位矢量i和 j分別指向天頂和繩系衛星系統的質心飛行方向。

根據圖1可知,系統質心和衛星的位矢分別為

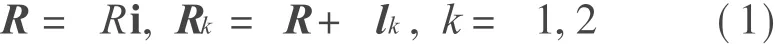
式中 l k=(-1)klk(i cosθ+ j sinθ)為衛星相對系統質心的位矢,其中lk=l[1-(mk+ 0.5mt)/m],m=m1+m2+mt為系統總質量。彈簧長度l=l0(1+X),l0為未變形的彈簧原長,X為彈簧的線彈性應變。系統的廣義主動力Qr和慣性力Q*r為

式中 _e=3.986×1014m3/s2為地球重力常數。Tk=k(l-l0)lk/lk為彈簧張力,k為彈性系數。vkr為衛星關于廣義坐標的偽速度。根據 Kane方程Qr+Q*r=0,可得狀態保持階段系統動力學方程

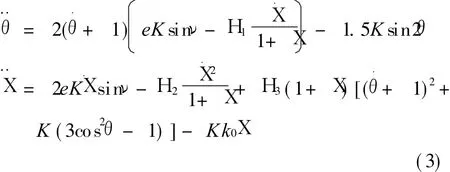
式中 “.”表示對真近點角ν的導數,K=(1+e cosν)-1,無量綱彈性系數 k0=ka3(1-e2)3/(m^_e),m^=m1(m2+mt)/m,a為橢圓軌道半長軸。其中式中~m=(m1+0.5mt)(m2+0.5mt)/m-mt/6。方程(3)為繩系衛星系統俯仰運動和系繩彈性變形相互耦合的自治非線性動力學系統,可能存在非線性共振現象。

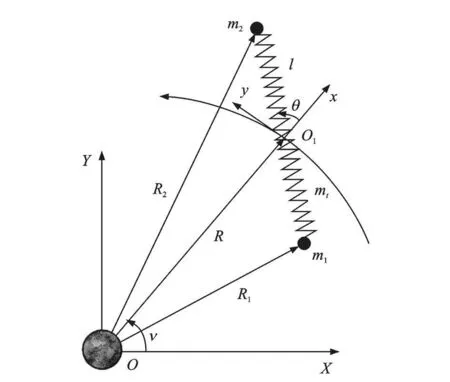
圖1 面內繩系衛星簡化模型Fig.1 A simp lifiedmodel for in-plane tethered satellite

2 共振條件分析

軌道偏心率的作用是在動力學方程中引入了一參數激勵。考慮小軌道偏心率情形以致可令e=T e,這里T為一小量。此時方程(3)的派生系統成為

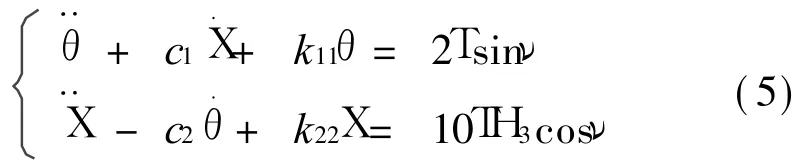
式中 c1=2H 1,c2=2H 3,k11=3,k22=k0-3H3。k 1,2為派生系統的固有頻率,滿足特征方程k4-(k11+

k22+c1 c2)k2+k11 k22=0,k 2＞ k 1。

考慮一次近似解的情況,系統固有頻率k1,2和激勵頻率k=1可能出現 2∶1內共振、2次超諧共振、1/2次亞諧共振以及參激組合共振的情況。選取兩組典型參數分析上述共振發生的可能性。取彈簧線密度 0.04 kg/m,長度 l=5 km,衛星質量m1=m2=100 kg。系統固有頻率k 1,2及其組合k2±k1隨參數k的變化如圖2(a),(b)所示。可見,k2±k 1始終遠離激勵頻率k=1。當時,k1≈2k,系統發生 1/2次亞諧共振,此時k2=2.110。取彈簧彈性系數,系統固有頻率k1,2及其組合k2±k1隨參數l的變化如圖2(c),(d)所示。k1始終在附近,k2遠大于固有頻率k1和激勵頻率k。可見,系統可能會發生2∶1內共振和 1/2次亞諧共振,但軌道偏心率所引起的亞諧共振并不會與系統內共振同時發生。

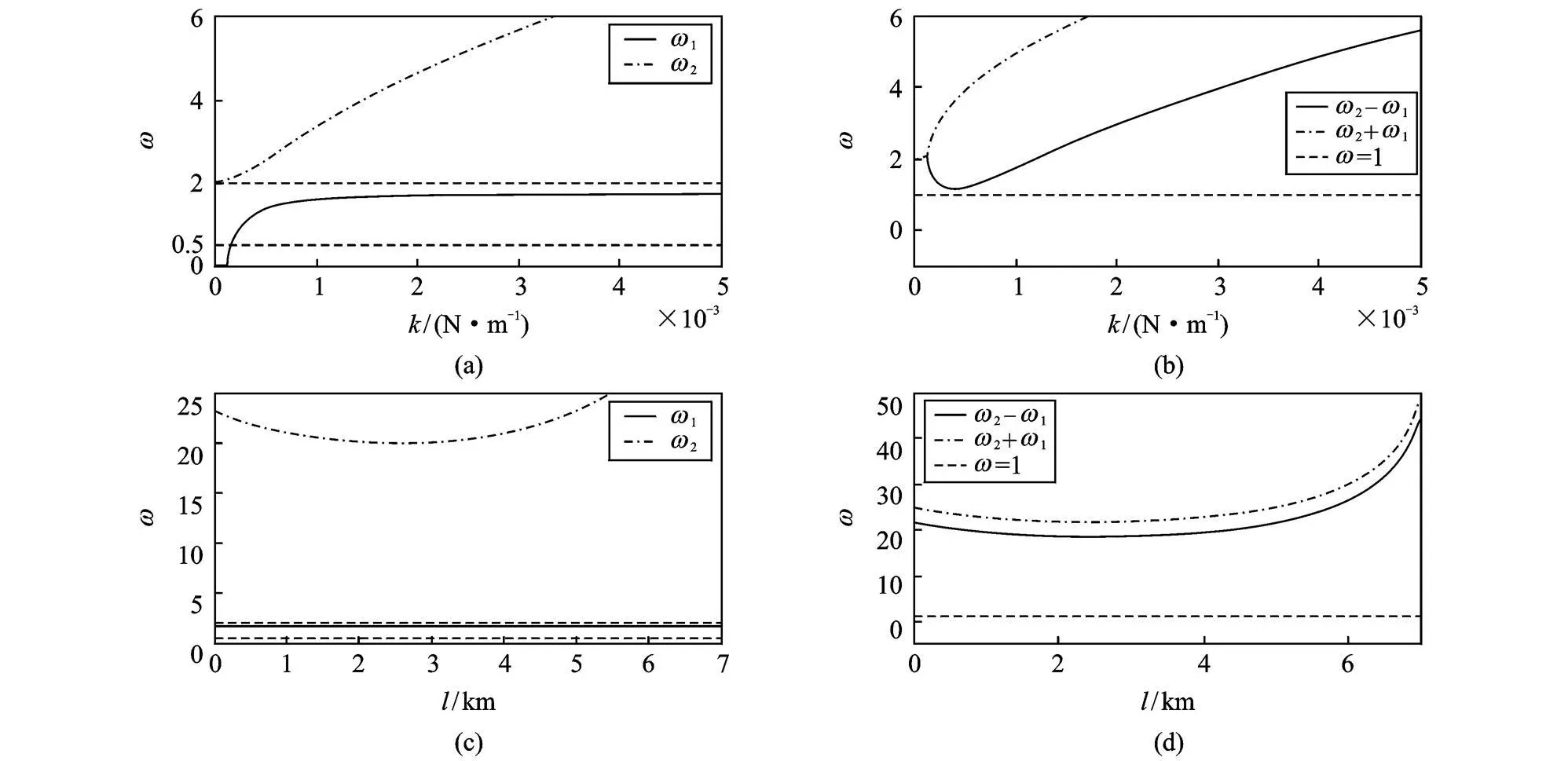
圖2 橢圓軌道共振分析Fig.2 Resonance analysis for ellipticalorbit

3 內共振分析

考慮到計入軌道偏心率后并不會影響系統的內共振,下面具體分析圓軌道內共振情形。此時系統動力學方程簡化為

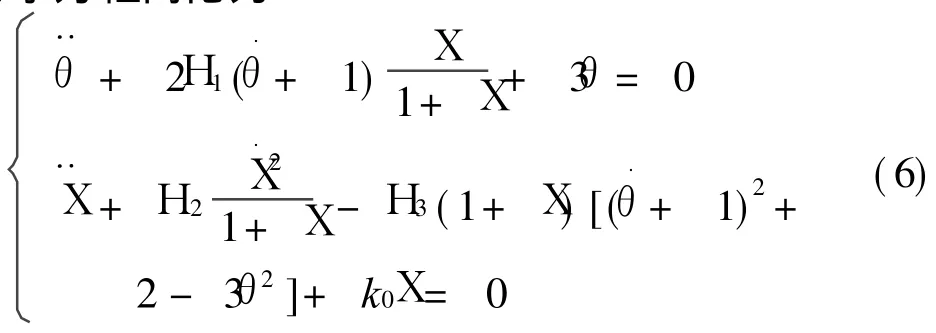
為消除常數項 ,可令a=X-2H3/H4,H4=k0-2H3。應用多尺度法求解系統(6)的一次近似解[11]。設

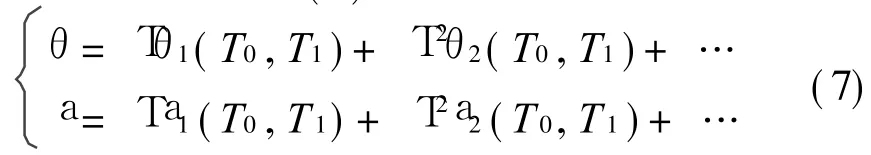
式中 T0=ν,T1=Tν。 將式(7)代入方程 (6)并比較方程兩邊T的同次冪系數得到

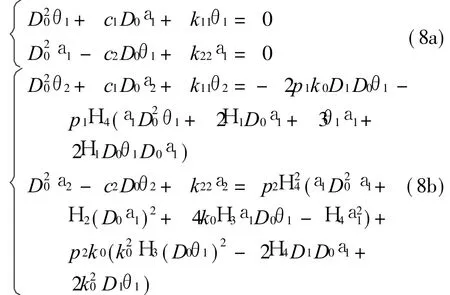
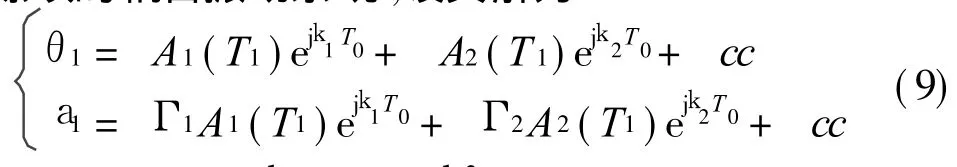
式中 Dr= ?/?Tr,r= 0,1。 p1=1/k0,p2=p1/H4,c1=2H 1H4/k0,c2=2k0H 3/H4。方程(8a)為一含有陀螺項的耦合振動系統,設其解為式中 Γr=j c2k r/(k22-k r2),r=1,2,cc代表前面各項的共軛,k 1,2為系統的固有頻率。將式(9)代入方程(8b)發現滿足k2=2k1+Te,e=O(1)時系統發生內共振。設方程(8b)的一個特解形如

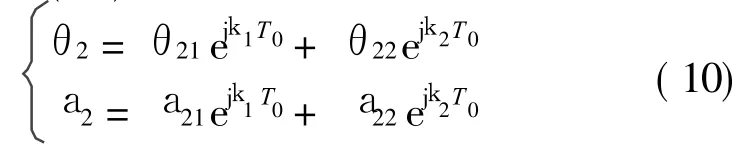
根據可解性條件,有

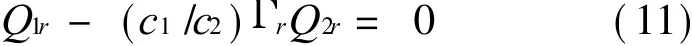
式中

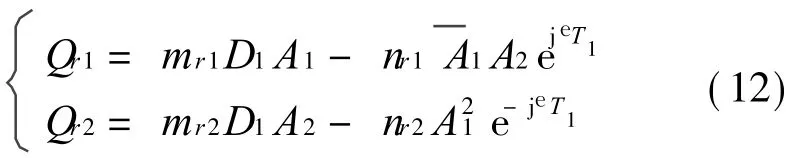
其中

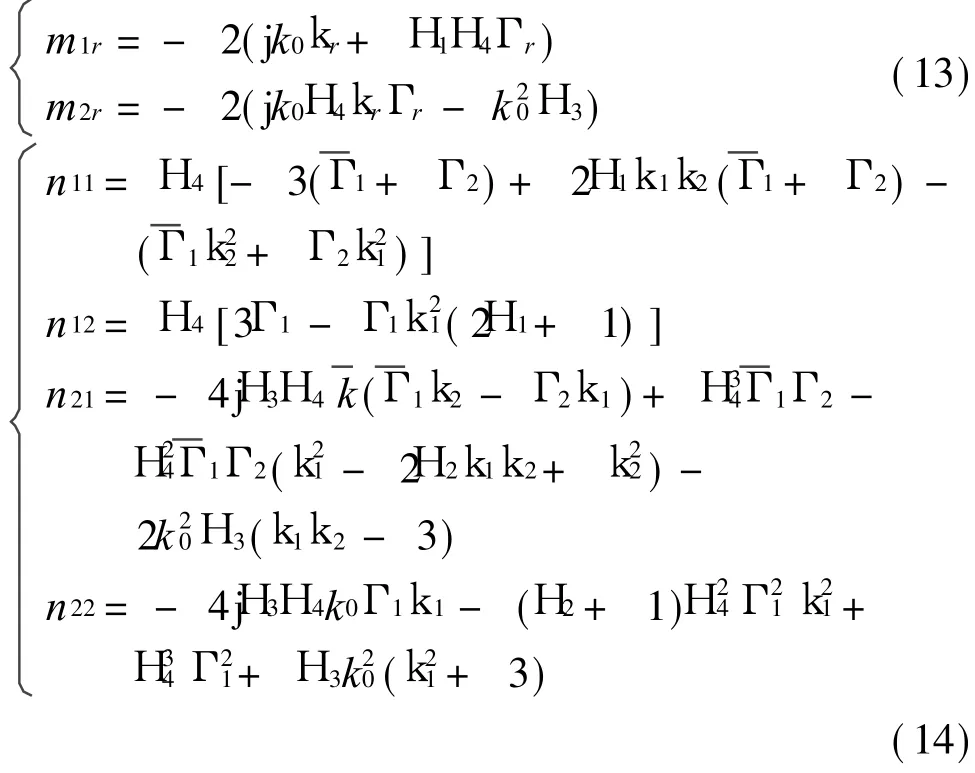
整理后獲得消除永年項的條件為

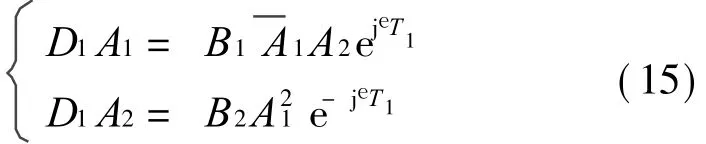
式中 Br= c2 n1r-c1Γr n2r/(c2m1r-c1Γrm 2r)。 令Ar(T1)=ar(T1)ejUr(T1)/2,代入方程(15)后分離實部和虛部,得到一階近似解振幅和相位滿足的微分方程組

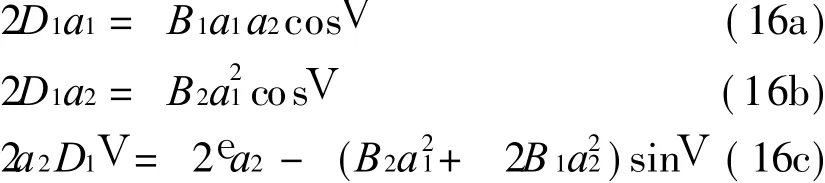
式中 V=U2-2U1+e T1。由方程 (16a)和 (16b)獲得全微分關系

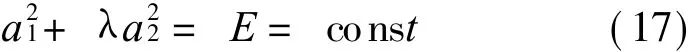
式中 λ=-B1/B2。 當λ＞ 0時 ,方程 (17)為 (a1,a2)平面上的橢圓;當λ＜0時,方程(17)為(a1,a2)平面上的雙曲線。本例中λ＞ 0。視a2為間接變量,由方程(16b)和 (16c)可得

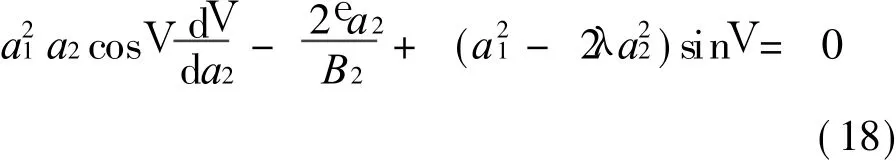
利用全微分關系將方程(18)整理后,有

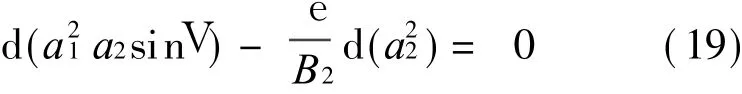
積分可得

a21a2 sin V-Be2a22= L= cons t (20)

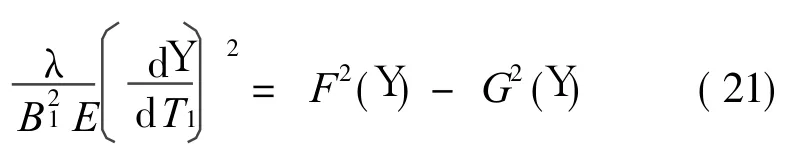
式中的一元函數F(Y)和G(Y)分別定義為

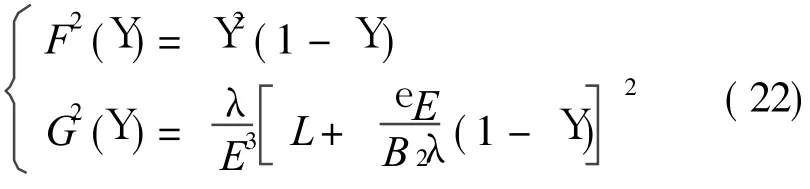
通常,函數 F(Y)與G(Y)有 3個交點。由于Y＞ 0,交點Y2和Y3對應于定常解D1 a1=0,即原系統的周期振動。當Y∈ (Y2,Y3),原系統作非周期振動,如圖3所示。引入變換Y3-Y=(Y3-Y2)sin2y,式(21)即可借助

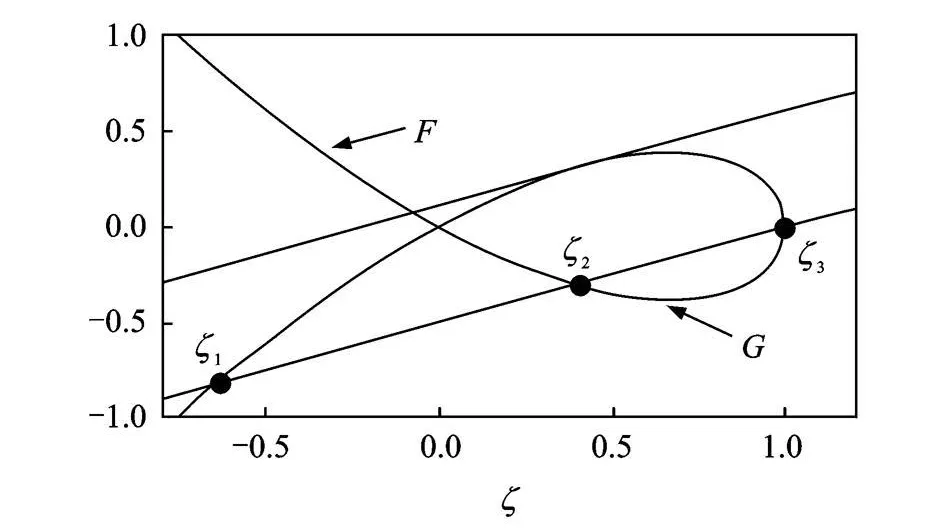
圖3 周期和非周期振動條件Fig.3 The conditions for periodic and non-periodic oscillations

Jacobi橢圓函數進行積分,從而給出

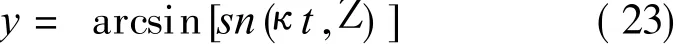
作為特例,當函數G(Y)與F(Y)的一支相切時(Y2=Y3),則

此時原系統對應周期振動。然而,任意小擾動都會導致函數 F(Y)與 G(Y)有3個交點,使其成為非周期振動。

4 算例研究

首先分析實現完全內共振的條件,即e=0。取無量綱參數H1=0.735,H 2=-1.326和 H3=0.526。當彈性系數 k=0.000 234 N/m或 k=0.000 408 N/m時,系統滿足 2∶1完全內共振條件,如圖4所示。

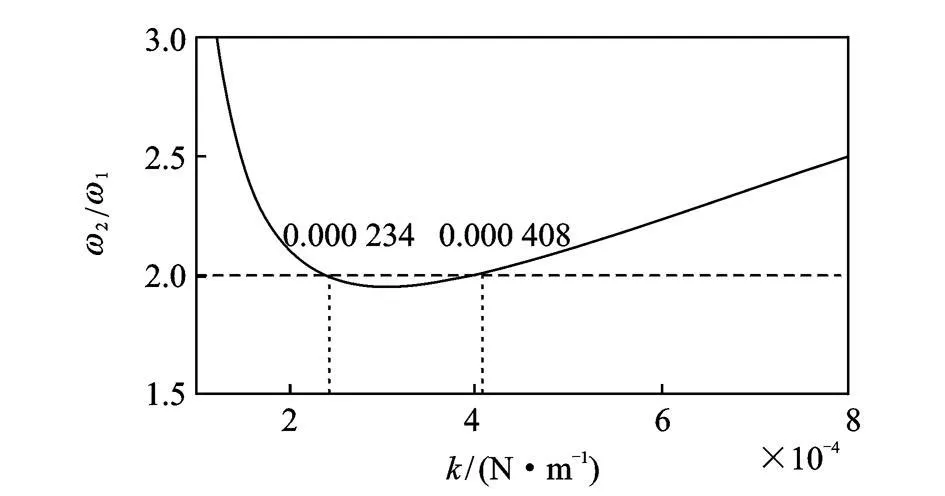
圖4 完全內共振條件Fig.4 The conditions for fully resonance

現取 k=0.000 5N/m,獲得k1=1.541和k2=3.230,即任一非完全內共振的情況進行數值研究。設振幅和相位初值為a10=0.04,T20=0.02和U10=U20=0.01。使用方程(16)和解析解(24)計算a1和a2的時間歷程,結果如圖5所示。結果顯示在ν=12 rad時,a1和a2分別達到最大值:a1的解析結果為 0.050 1,數值結果為 0.050 8;a2的解析結果為0.017 4,數值結果為0.017 2。在整個時間歷程內,a1的解析結果與數值結果的誤差絕對值始終小于 0.001,a2的誤差絕對值則始終在0.000 5以內。解析結果和數值結果吻合較好。從圖5可見,兩種模態表現為異步振動,能量發生相互轉換:一個模態的能量減小時,另一個模態的能量增大。

圖5 周期振動響應Fig.5 Periodic oscillation responses versusν

取參數W=k2-2k1,圖6給出了振幅最大值隨參數W的變化關系。由圖6(a)可知,a1的最大振幅為0.65,發 生在 W= 0.01,此 時彈性 系數 k=0.000 419 N/m。 從圖6(b)可見,當W∈ (-0.028,0.038),即k∈ (0.000 384,0.000 434)N/m時 ,a2的振幅出現了飽和現象,始終保持在初值 0.02上。在參數W接近零時,解析解和數值解吻合最好。

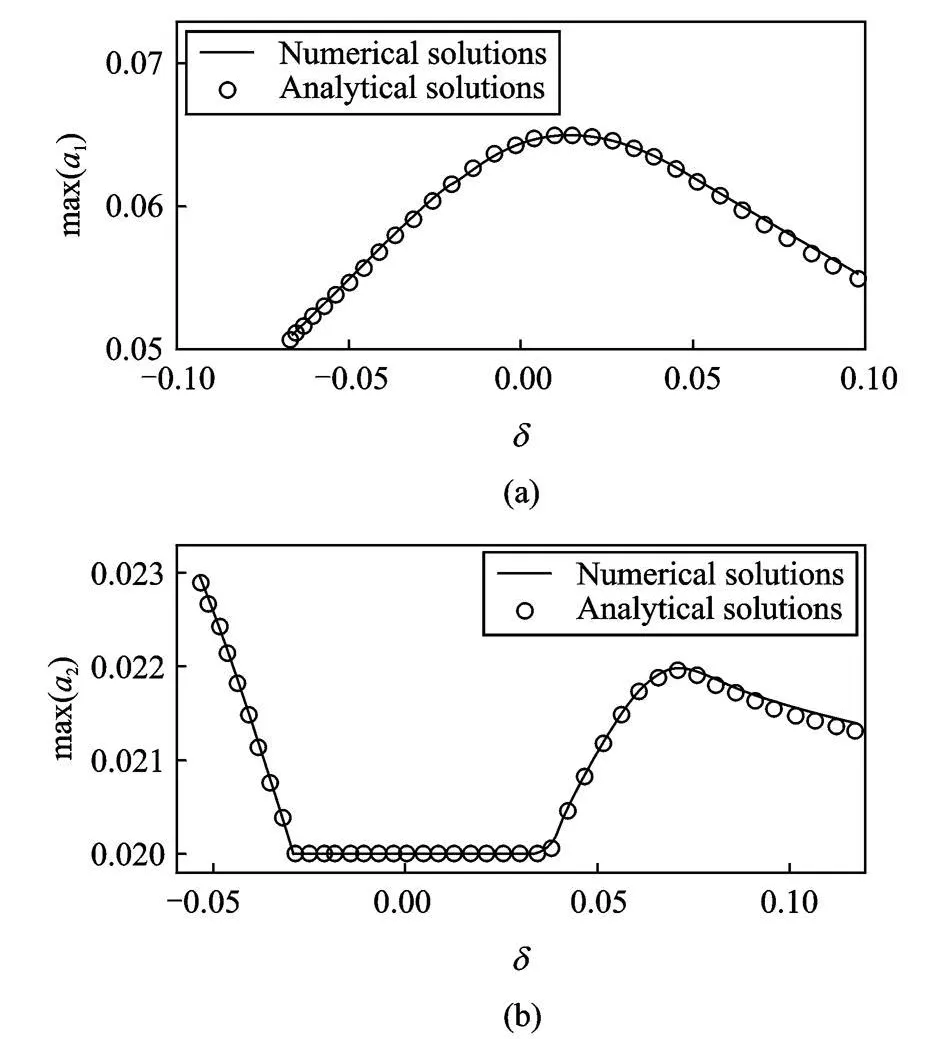
圖6 參數W對周期振動最大幅值的影響Fig.6 The effect of parameter W on maximum of periodic oscillation

非線性振動周期依賴于振幅。給定a20=0.01,研究a10對振動周期的影響,圖7(a)給出了a10變化時數值積分得到的模態振幅運動的周期T與解析表達式計算得到的周期的對比。可以看出二者吻合較好。注意到a10=0.04時,解析解得到的周期 T=40.8 rad和數值積分得到的周期T=39.7 rad均與圖6給出的算例一致。圖7(b)給出了根據解析表達式得到的周期隨初始振幅的變化情況。從圖7(b)可見,模態振幅運動的周期隨a10的增大而減小,隨a20的增大而增大。

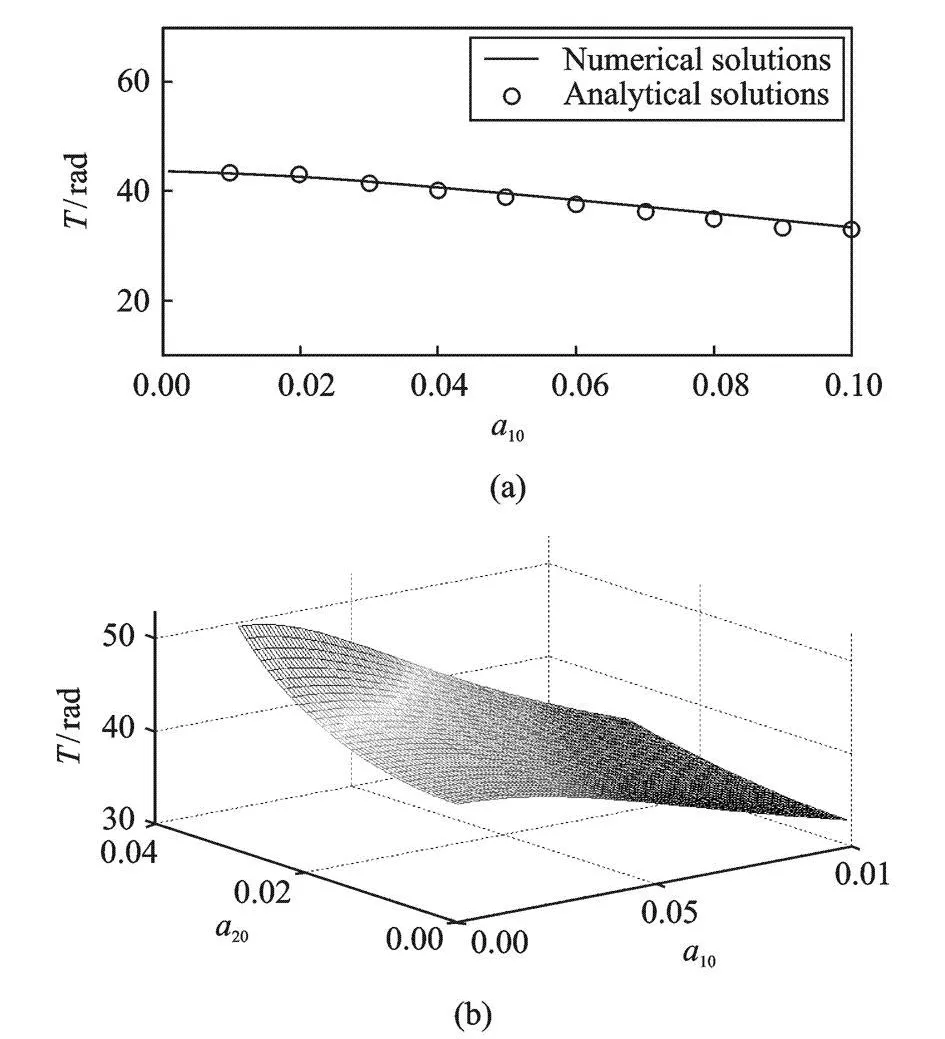
圖7 初始模態幅值對周期的影響Fig.7 The effect of initia lmode amp litudes on the period

5 結 論

考慮彈性的繩系衛星系統可發生非線性 2∶1內共振,其模態幅值可借助Jacobi橢圓函數表示。結果表明,系統的周期運動只是臨界穩定,任何微小的擾動都會使其成為非周期運動。在非線性共振時,模態振幅的周期與其初值有關,振動能量在兩個模態幅值間相互傳遞。在一個小的調諧參數范圍上,有一個模態振幅會出現飽和現象。

[1] Cosmo M L,Lorenzini E C.Tethers in Space Handbook(3rd ed.)[M].W ashington DC,NASA,1997.

[2] Modi V J,Lakshmanan P K,M isra A K.Dynam ics and contro l of tethered spacecraft:a brief overview[A].A IAA Dynam ics Specialist Conference[C].Long Beach,California,United States,1990.

[3] Kumar K D.Review of dynam ics and control of nonelectrodynam ic tethered satellite systems[J].Journal of Spacecraftand Rockets,2006,43(4):705—720.

[4] Cartmell M P,M ckenzie D J.A review of space tether research[J]. Progress in Aerospace Sciences,2008,44(1):1—21.

[5] W en H,Jin D P,Hu H Y.Advances in dynam ics and control of tethered satellite systems[J].Ac ta Mechanica Sinica,2008,24(3):229—241.

[6] Nixon M S.Nonlinear dynam ics and chaos of tethered satellite system[D].PhD Thesis,Department of Mechanical Engineering M cGill University,Montreal,1996.

[7] Fujii H A,IchikiW.Nonlinear dynamics of the tethered subsatellite system in the station keeping phase[J].Journal of Guidance,Contro l,and Dynamics,1997,20(2):403—406.

[8] M isra A K,Nixon M S,ModiV J.Nonlinear dynamics of two-body tethered satellite system s: Constant length case[J].Journal of the Astronautical Sciences,2001,49(2):219—236.

[9] Celletti A,Sidorenko V V.Some properties of the dumbbell satelliteattitude dynam ics[J].Celestial Mechanics and Dynamical Astronomy,2008,101(1-2):105—126.[10]Sidorenko V V,Celletti A A.“ Spring-mass” modelof

tethered satellite system s:p roperties of p lanar periodic motions[J].CelestialMechanics and Dynam ical A stronomy,2010,107(1-2):209—231.

[11]Nayfeh A H,Mook D T.Non linear Oscillations[M].New York:W iley InterScience,1979.