一類出現(xiàn)在燃燒理論中的奇攝動邊值問題

方曉玲 ，周 健 ，劉樹德

(1.安徽大學 數(shù)學科學學院，安徽 合肥230601；2.安徽師范大學 數(shù)學系，安徽 蕪湖 241000）

1 引 言

奇異攝動理論和方法是當前解決工程技術和科學問題的主要數(shù)學工具之一，在天體力學、流體力學、量子力學、彈性力學、化學反應理論、燃燒理論、光的傳播和非線性振動等學科得到了廣泛的應用，[1-7]例如 Willams，[1]章國華和 Howes[4]討論了幾類出現(xiàn)在燃燒理論中的奇攝動Dirichlet問題。

本文在此基礎上考慮如下形式的奇攝動Robin問題

其中y為燃燒火焰的密度，ε為反應速度的擴散率，它是一個正的小參數(shù)，t為燃燒位置，A≥2和B≥1為常數(shù)，n≥1為正整數(shù)。

我們通過選取適當?shù)木哂羞吔鐚有再|(zhì)和角層性質(zhì)的函數(shù)構造出一對界定函數(shù)，應用微分不等式理論證明問題(1)-(3)存在具有角層性質(zhì)的解，并給出解的漸近估計，為此需要用到如下引理。

引理[4]： 考慮二階非線性常微分方程Robin問題)))

其中函數(shù) f在區(qū)域 D=[a，b]×R2中連續(xù)， f(t，y，z)=O （|z|2） （（|z|） →+∞）。 p，q 是 非 負 常 數(shù)且不同時為零。 假設存在函數(shù) α(t)，β(t)∈C2[a，b]使得

及微分不等式

則問題(4)-(6)在區(qū)間[a，b]上存在一個解 y=y(t)，并成立不等式

α(t)，β(t)通常稱為問題(4)-(6)的一對界定函數(shù)。1968年Jackson[8]減弱了對界定函數(shù)的要求：若在[a，b]上存在分劃{t}：a=t0＜t1＜…＜tn=b，使得 α，β∈C2[ti-1，ti](i=1，2，…，n)（在左、右端點處的導數(shù)分別指右導數(shù)和左導數(shù)），即 α（t），β（t）為[a，b]上分段 C2類函數(shù)，且在

其中K2為確定的常數(shù)。當t0=0時，(10)寫為

及

則引理的結論仍成立。

2 構造具有邊界層和角層性質(zhì)的函數(shù)

由于退化解u(t)=|t|的導數(shù)在t=0處有躍度u'(0+)-u'(0-)=2，需要在t=0處構造具有角層性質(zhì)的函數(shù)。在(14)中令

當反應率ε=0時，問題(1)-(3)退化方程

可得

于是

從而得到

有解 u1=-t和 u2=t。選取方程(7)在[-1，1]上的一個穩(wěn)定解 u(t)=|t|。

助方程

方程(8)在I上具有如下形式的代數(shù)型漸近角層解

其中C為任意常數(shù)，λ，μ是與t0有關的常數(shù)。將(9)代入(8)得

它是一個在t=0處具有角層性質(zhì)的函數(shù)。

從而得出

3 解的存在性及解的漸近估計

于是

應用微分不等式理論，我們來證明解的存在性，并給出解的漸近估計。

定理：設 A≥2，B≥1，則燃燒問題(1)-(3)在[-1，1]上存在一個解y(t，ε)具有如下形式的漸近估計式：

當 t0=-1 時，(10)寫為

注意到問題(1)-(3)的解與(7)的穩(wěn)定解u(t)=|t|在

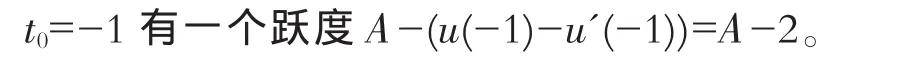
令

由(11)得

其中 0＜ε＜＜1，n≥1 為正整數(shù)。

證明：構造界定函數(shù) α(t，ε)和 β(t，ε)如下

其中 L(t，ε)，R(t，ε)和 M(t，ε)分別由(12)，(13)和(15)確定，r為待定的正常數(shù)。由(17)可知

且容易推出

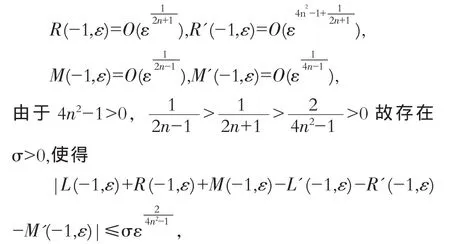
于是

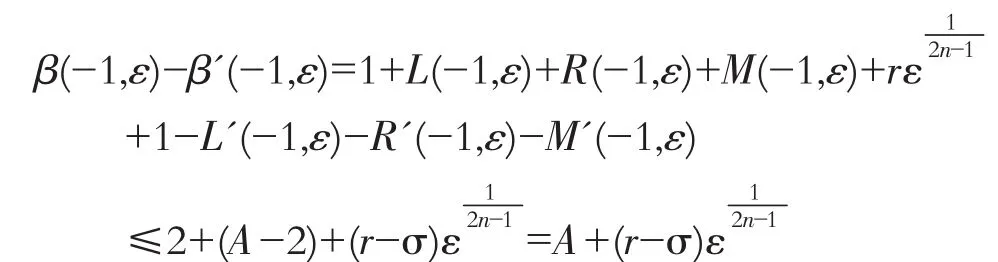
選擇 r≥σ，便有

同理可得

接著我們證明在 t∈(-1，0)∪（0.1）上

事實上，由于

可得

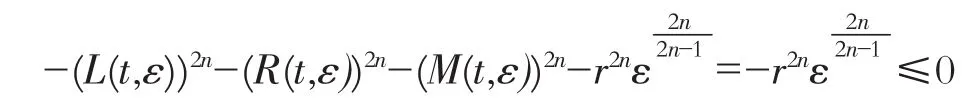
即(22)成立。

注意到函數(shù) α(t，ε)和 β(t，ε)在 t=0 不可導，但顯然成立

根據(jù)引理及Jackson[8]推廣的微分不等式理論，從(18)-(23)推出，對充分小的正數(shù) ε，問題(1)-(3)在[-1，1]上存在一個解 y(t，ε)，并滿足不等式

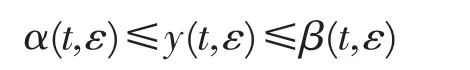
因此漸近估計式(16)成立，定理證畢。

[1]Willams，F(xiàn).A.Theory of combustion in laminar flows[J].Ann Rev Fluid Mech，1971，3:171-188.

[2]江濤，劉樹德.一類出現(xiàn)在化學反應器理論中的奇攝動邊值問題[J].黃山學院學報，2011，13（5）：13-15.

[3]Nayfeh，H，Introduction for Perturbation Techniques[M].New York:John Wiley&Sons，1981:394-432.

[4]Chang K.W，and Howes F.A Nonlinear Singular Perturbation Problems：Theory and Applications[M].New York:Spring Verlag，1984:153-208.

[5]林宗池，周明儒.應用數(shù)學中的攝動方法[M].南京:江蘇教育出版社，1995:123-126.

[6]de Jager，E.M.and Jiang Furu，The Theoy of Singular Perturbations[M].Amsterdam:Elsvier.1996:276-291.

[7]劉樹德，魯世平，姚靜蓀，等.奇異攝動邊界層和內(nèi)層理論[M].北京：科學出版社，2012:124-151.

[8]Jackson，L K，Subfunctions and Second-Order Ordinary Differential Inequalities[J].Adv in Math，1968，(2):307-363.