質點在不同初始條件下做有心力運動的探討

江昌龍

（黃山學院 信息工程學院，安徽 黃山245041）

0 引 言

在理論力學[1]教材書中有專門的章節介紹了質點在有心力作用下的運動，推導出比耐公式和能量方程，并討論萬有引力和庫侖引力兩種有心力模型，對比耐公式和能量方程進行了初步求解，但文中沒有確定求解結果中的系數，而且也沒有討論方程在什么樣的情況下有解以及說明初始條件的不同會對結果造成什么樣的影響。事實上，方程中的系數是由初始條件來確定的，若初始條件給定，質點在有心力作用下的運動也將確定。初始條件不同，運動結果也將大相徑庭，基于這方面的考慮，本文系統全面闡述了質點在不同初始條件下做有心力作用下的運動探討，對與平方成反比力的有心力模型做了深刻而細致的計算，對教材中的內容做了擴展和補充。

一般來說，對于二體運動問題，如果其中一方位置固定或者質量遠大于另一方，就可以化為單質點運動問題，也就是本文所討論的問題模型。此問題模型的探討在天體運動、人造衛星的發射，微觀粒子在靜電場中的運動等相關一類問題都有廣泛的應用。

1 質點在極坐標系下的動力學方程

在初始位置給出一定的初始速度，質點在有心力作用下開始運動，以r(r＞0)代表極徑，θ代表極角，如圖1所示，則在極坐標系下質點運動的動力學方程可以表示為：

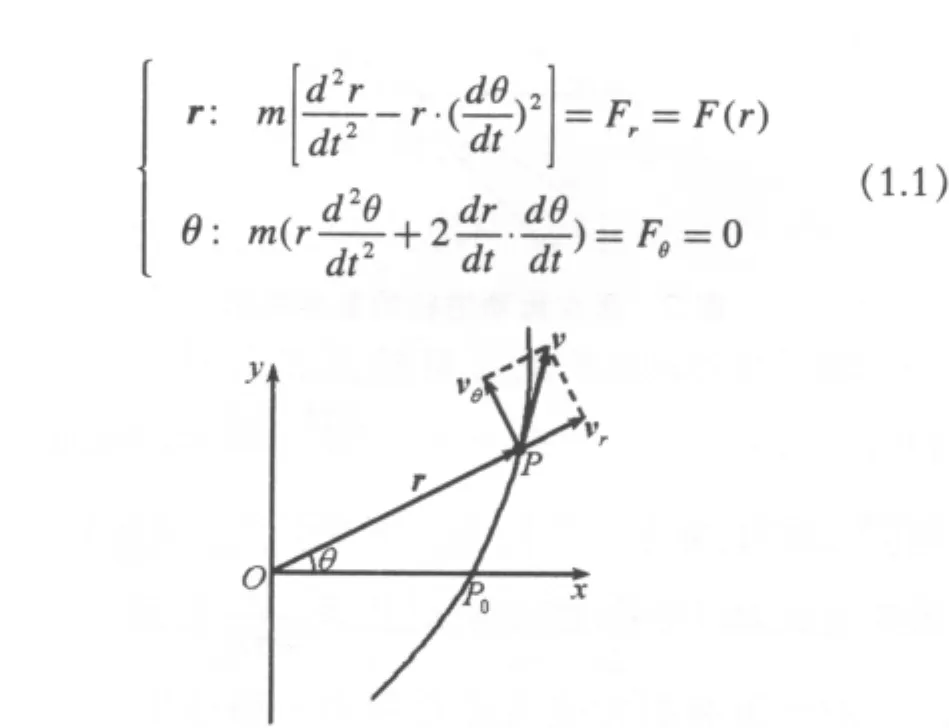
圖1 極坐標系下質點在有心力作用下的運動

4 總結

以上討論了質點在與距離平方成反比的有心力作用的條件下由于初始條件的不同而造成對運動結果及對運動軌跡的影響。

1.應用比耐公式也可以計算質點的運動方程，但采用能量方程更具廣泛意義。計算結果表明，質點運動的軌跡曲線與初始條件的r0，v0和α角都有關系。

2.在0＜α＜π時，可以根據初始條件把質點的運動的在極坐標系下的運動學方程比較容易得算出來。在α=0或π時，要根據初始條件計算質點在有心力作用下沿直線運動時位置與時間的關系時，該方程難以把位置表示成時間的函數關系，但是可以比較容易把時間表示成位置的函數關系。

[1]周衍柏.理論力學教程[M].北京：高等教育出版社，1986.