矩陣方程組(AX=B, XC=D)的Hermitian反自反反Hermitian反自反最小二乘解及其最佳逼近

周 碩, 王 霖, 王 雯

(東北電力大學 理學院, 吉林 吉林 132012)

0 引 言

近年來, 關于矩陣方程組AX=B,XC=D求解問題的研究已有許多結果[1-5]. 本文研究矩陣方程組AX=B,XC=D的Hermitian反自反(反Hermitian反自反)最小二乘解.

記Cm×n表示m×n階復矩陣集合,UCn×n表示n×n階酉陣集合;AH,A+和‖A‖分別表示矩陣A的共軛轉置矩陣、 Moore-Penrose廣義逆矩陣和矩陣A的Frobenius范數;In表示n階單位矩陣;S表示反序單位陣, 即In=(e1,e2,…,en), 則S=(en,en-1,…,e1)； 對全體A,B∈Cm×n, 定義內積〈A,B〉=tr(BHA), 對?A,B∈Cm×n,A*B=(aijbij)表示矩陣A和B的Hadamard乘積,Cm×n是完備的內積空間并且該內積空間下的矩陣范數為Frobenius范數.

定義1如果一個n×n矩陣J滿足JH=J,J2=In, 則稱J為n階廣義反射矩陣.

定義2給定一個廣義反射矩陣J, 矩陣A∈Cn×n是Hermitian反自反矩陣當且僅當AH=A,A=-JAJ. 所有n階Hermitian反自反矩陣的全體記為HAJn×n.

定義3給定一個廣義反射矩陣J, 矩陣A∈Cn×n是反Hermitian反自反矩陣當且僅當AH=-A,A=-JAJ, 所有n階反Hermitian反自反矩陣的全體記為AHAJn×n.

問題1給定A,B∈Cm×n,C,D∈Cn×s, 求X∈HAJn×n(或X∈AHAJn×n), 使得

‖AX-B‖2+‖XC-D‖2=min.

這里SE是問題1的解集合.

本文研究矩陣X∈HAJn×n(或X∈AHAJn×n)的特殊性質, 應用這些性質及文獻[4-8], 得到了問題1的一般解, 并當SE為非空集合時, 給出了問題2的解.

當J=S時, 本文研究結果可轉化為矩陣方程組AX=B,XC=D的對稱次反對稱(反對稱次對稱)最小二乘解. 當C,D=0時, 本文研究結果可轉化為矩陣方程AX=B的對稱次反對稱(反對稱次對稱)最小二乘解[9-10].

1 問題1的求解

先討論n×n廣義反射矩陣J的結構和集合HAJn×n(AHAJn×n). 因為J2=In, 所以J可能的特征值只有+1和-1. 假設特征值+1是r重的. 因為JH=J, 則+1對應的特征子空間也是r維的, 它的正交補空間(顯然是n-r維的)是-1對應的. 因此, 易得:

引理1給定一個n×n廣義反射矩陣J, 則存在酉矩陣U, 使得

(1)

由定義2、 定義3及引理1, 可得矩陣集合HAJn×n和AHAJn×n的如下結果.

引理3給定矩陣A∈Cn×n, 廣義反射矩陣J的譜分解由式(1)給出, 則矩陣A∈AHAJn×n當且僅當

證明: 可參考引理2的證明.

引理4[7]給定矩陣A,B∈Ch×r,C,D∈Cr×l, 矩陣A和C的奇異值分解如下:

則極小化問題‖AX-B‖2+‖XC-D‖2=min, 解的形式為

?X22∈C(r-r1)×(r-s1),

由引理1和引理2知, 求解矩陣方程組AX=B,XC=D的Hermitian反自反解可等價地表示為

記

(2)

這里:A1,B1∈Cm×r;A2,B2∈Cm×(n-r);C1,D1∈Cr×s;C2,D2∈C(n-r)×s, 可得

(3)

求解式(3)等價于求解矩陣方程組AX=B,XC=D的Hermitian反自反解.

同理, 由引理1和引理3知, 求解矩陣方程組AX=B,XC=D的反Hermitian反自反解等價于求解

(4)

(5)

(6)

(7)

(8)

(9)

(10)

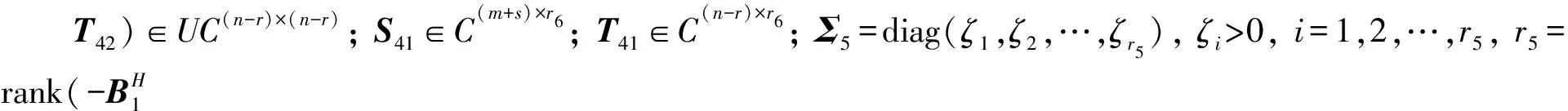
由于矩陣方程組AX=B,XC=D等價于式(3)或(4). 因此易得如下定理.

定理1如果AU,BU,UHC,UHD的分塊形式由式(2)給出, 則問題1在HAJn×n中的最小二乘解可以表示為

(11)

(12)

證明: 由引理1和引理2有

因此, 問題1等價于

(13)

由引理4與式(5)～(8)可知,X12可以表示為式(12), 進而, 可以得到問題1在HAJn×n中解的表達式(11).

定理2如果AU,BU,UHC,UHD的分塊形式由式(2)給出, 則問題1在AHAJn×n中的最小二乘解可表示為

(14)

(15)

證明: 類似定理1的證明.

2 問題2的求解

由式(11), 易證問題1有解X∈HAJn×n(AHAJn×n), 則SE為一閉凸集. 因此, 對任意給定矩陣X*∈Cn×n, 問題2存在X*的唯一最佳逼近解.

定理3對任意矩陣X*∈Cn×n, 其他符號與定理1相同, 如果

(16)

(17)

這里

(18)

證明: 當SE非空時, 由式(11)易證SE是閉凸集,Cn×n在Frobenius范數下構成Banach空間, 因此問題2有唯一的解, 故有

可知問題2的‖X*-X‖2=min等價于

(19)

進而

這里

證明: 類似于定理2及定理1的證明.

例1已知矩陣

根據定理1和定理3, 應用MATLAB程序, 可計算問題2的最佳逼近解為

[1] Mitra S K. A Pair of Simultaneous Linear Matrix EquationsA1XB1=C1,A2XB2=C2and a Matrix Programming Problem [J]. Linear Algebra and Its Appl, 1990, 131(1): 107-123.

[2] Chu K W E. Singular Value and Generalized Singular Value Decomposition and the Solution of Linear Matrix Equation [J]. Linear Algebra and Its Appl, 1987, 88/89: 83-98.

[3] CHEN Yong-lin. The Iterative Method for Solving the Set of Matrix EquationsAX=C,XB=D[J]. Journal of Nanjing Normal University: Natural Science, 1999, 22(1): 1-3. (陳永林. 求解矩陣方程組AX=C,XB=D的迭代法 [J]. 南京師大學報: 自然科學版, 1999, 22(1): 1-3.)

[4] LI Fan-liang, HU Xi-yan, ZHANG Lei. The Generalized Reflexive Solution for a Class of Matrix Equations(AX=B,XC=D) [J]. Acta Mathmatica Scientia: Ser B, 2008, 28(1): 185-193.

[5] LI Fan-lian, HU Xi-yan, ZHANG Lei. The Generalized Anti-reflexive Solution for a Class of Matrix Equations (BX=C,XD=E) [J]. Computational and Applied Mathematics, 2008, 27(1): 31-46.

[6] PENG Zhen-yun, HU Xi-yan. The Reflexive and Anti-reflexive Solutions of the Matrix EquationAX=B[J]. Linear Algebra and Its Appilications, 2003, 375(1): 147-155.

[7] ZHANG Lei, XIE Dong-xiu. A Class of Inverse Eigenvalue Problem [J]. Acta Mathematiea Scientia, 1993, 13(1): 94-99. (張磊, 謝冬秀. 一類逆特征值問題 [J]. 數學物理學報, 1993, 13(1): 94-99.)

[8] PENG Zhen-yun. The Inverse Eigenvalue Problem for Hermitian Anti-reflexive Matrices and Its Approximation [J]. Applied Mathematics and Computation, 2005, 162(3): 1377-1389.

[9] XIE Dong-xiu, LIAO An-ping. The Least-Squares Solution of Inverse Problerm over Anti-symmetric and Persymmetric Matrices [J]. Journal of Numerical Methods and Computer Applications, 2003(4): 304-313. (謝冬秀, 廖安平. 一類反對稱次對稱矩陣反問題的最小二乘解 [J]. 數值計算與計算機應用, 2003(4): 304-313.)

[10] SHENG Yan-ping, XIE Dong-xiu. The Solvability Conditions for the Inverse Problem of Symmetric and Sub-anti-symmetric Matrices [J]. Mathematica Numerica Sinica, 2004, 26(1): 73-80. (盛炎平, 謝冬秀. 一類對稱次反對稱矩陣反問題解存在的條件 [J]. 計算數學, 2004, 26(1): 73-80.)