一類優(yōu)化問題的動約束組合同倫算法

王 艷, 王秀玉, 劉慶懷

(長春工業(yè)大學(xué) 基礎(chǔ)科學(xué)學(xué)院, 長春 130012)

同倫算法由于具有大范圍收斂性而成為證明非線性問題解存在的有效方法之一, 同倫算法不僅能獲得解的存在性, 而且能進(jìn)行求解計(jì)算, 既適用于凸優(yōu)化問題, 也適用于非凸、 非線性優(yōu)化問題. 文獻(xiàn)[1-2]利用同倫方法得到了互補(bǔ)問題有解的條件; 文獻(xiàn)[3-4]對多目標(biāo)優(yōu)化和變分不等式問題分別構(gòu)造了同倫方程, 并獲得了問題的解; 文獻(xiàn)[5-7]研究了非線性優(yōu)化問題的組合同倫算法; 文獻(xiàn)[8-9]研究了光滑非凸優(yōu)化的動約束組合同倫算法. 但利用組合同倫方法求解非凸、 非線性優(yōu)化問題, 還需要條件： 可行域滿足法錐條件, 或者滿足擬法錐條件, 或者滿足偽法錐條件. 當(dāng)可行域不滿足各類法錐條件時, 利用組合同倫方法求解非凸非線性優(yōu)化問題的研究結(jié)果目前較少. 本文利用文獻(xiàn)[9]中的動約束技術(shù), 給出了當(dāng)可行域不滿足各類法錐條件時, 一類優(yōu)化問題的動約束組合同倫算法.

1 預(yù)備知識

設(shè)φ:D?Rm→Rn是光滑映射, 對任意的y∈Rn, 記φ-1(y)={x∈Dφ(x)=y}為y在映射φ下的逆像. 如果φ在x(0)∈D處的Jacobi矩陣?φ(x(0))/?x行滿秩, 則稱x(0)是映射φ的正則點(diǎn); 否則稱x(0)是φ的臨界點(diǎn). 如果對所有的x(0)∈φ-1(y(0))都是映射φ的正則點(diǎn), 則稱y(0)是映射φ的正則值; 否則稱y(0)是φ的臨界值.

引理1(參數(shù)化的Sard定理)[10]設(shè)V?Rn,U?Rm均為開集,φ:V×U→Rp是Cr映射, 這里r>max{0,m-p}. 如果0∈Rp是φ的一個正則值, 則對幾乎所有a∈V,0是φ(a,·)的一個正則值.

引理2(逆映像定理)[11]如果0是映射φ(a,·)的正則值, 則逆映射φ-1(a,·)由有限條一維光滑流形組成.

引理3(一維流形分類定理)[11]一維帶邊光滑流形的每個連通分支, 或者微分同胚于單位圓周, 或者微分同胚于區(qū)間(0,1]或(0,1)或[0,1].

考慮問題(P)：

記I(x)={i∈M:gi(x)=0},g(x)=(g1(x),g2(x),…,gm(x))T, ▽g(x)=(▽g1(x),▽g2(x),…,▽gm(x)),Ω={x∈Rn:gi(x)≤0,i∈M},Ω0={x∈Rn:gi(x)<0,i∈M}, ?Ω=ΩΩ0.

假設(shè)條件如下:

(H1)f,gi(i∈M)∈Cr(r≥3);

(H2)Ω0非空且Ω有界連通;

(H3) 對任意的x∈?Ω, {▽g(x)i∈(x)}是正獨(dú)立的.

記gi(x,u)=gi(x),i∈M;Ω(μ)={x∈Rngi(x,μ)≤0,i∈M∪{m+1}};Ω0(μ)={x∈Rngi(x,μ)<0,i∈M<∪{m+1}};g(x,μ)=(g1(x),g2(x),…,gm(x),gm+1(x,μ))T. 通過選取一個適當(dāng)?shù)膭蛹s束函數(shù)gm+1(x,u), 使得如下假設(shè)成立：

無解, 其中: ?Ω(μ)=Ω(μ)Ω0(μ);I(x,μ)={i∈M∪{m+1}gi(x,μ)=0};

(H5)gm+1(x,μ)關(guān)于x及μ充分光滑, ?μ∈[0,1]θ,Ω0(μ)非空,Ω(μ)有界且Ω(0)=Ω, ?x∈?Ω(μ), {▽xgi(x,μ)i∈I(x,μ)}正獨(dú)立;

2 主要結(jié)果

(1)

其中:y=(y1,y2,…,ym,ym+1)T;g(x,μ)=(g1(x,μ),g2(x,μ),…,gm+1(x,μ))T;

(2)

問題(P)的K-K-T方程為

(3)

方程(2) 的解必為方程(3)的解, 且顯然有H(ω(0),ω(0),1)=0.

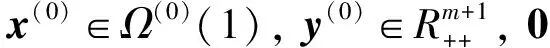
證明:H(ω,ω(0),μ)的Jocobi矩陣記為H′(ω,ω(0),μ),

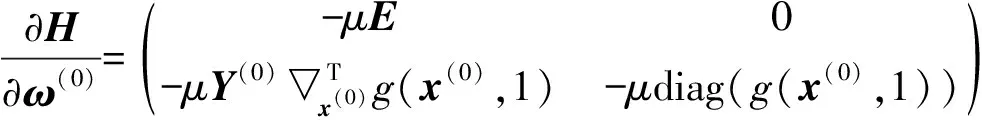
從而H′(ω,ω(0),μ)行滿秩, 由引理1知,0是H(ω,ω(0),μ)的正則值. 又由引理2知,H-1(0)所含曲線是光滑的, 且H(ω(0),ω(0),1)=0, 因而, 存在一條起始于(ω(0),1)的光滑曲線, 記為Γω(0).

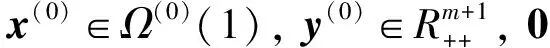
證明: 用反證法. 假設(shè)光滑曲線Γω(0)無界, 則必存在點(diǎn)列(x(k),y(k),μk)∈Γω(0), 使得‖(x(k),y(k),μk)‖→∞(k→∞). 由同倫方程(1)的第二式得

(4)

(5)

將式(5)整理如下：

情形1)μ*=1. 式(6)兩邊取極限得

與(H6)矛盾.

式(7)兩邊取極限得

(8)

證明:Γω(0)的存在性及有界性由引理4和引理5可知. 又由引理3知,Γω(0)或微分同胚于單位圓周, 或微分同胚于單位區(qū)間(0,1]. 因?yàn)?/p>

其中:

3)μ*=0, (x(*),y(*))∈Ω×R+, ‖y(*)‖<∞.

3 路徑跟蹤算法及算例

算法1Euler-Newton法[12].

輸入ω(0), 選取初始步長h0>0, 正數(shù)J1=2,J2=5及小正數(shù)ε1,ε2,α,β∈(0,1), 并且令μ0=1,k=0.

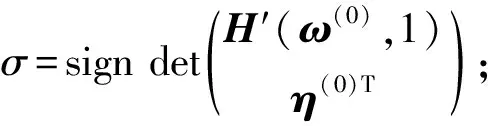
2) 計(jì)算預(yù)估點(diǎn)(ω(k+1,0),μk+1,0)=(ω(k),μk)+αlhkη(k), 其中l(wèi)是使得(ω(k+1,0)μk+1,0)∈Ω0×(0,1]成立的最小正整數(shù).

3) 計(jì)算校正點(diǎn)(ω(k+1),μk+1): 若使(ω(k+1,0),μk+1,0)∈Ω0×(0,1]成立的最小正整數(shù)j≤J2, 且‖H(ω(k+1, j),μk+1, j)‖>ε1, 則

(ω(k+1, j),μk+1, j)=(ω(k, j-1),μk, j-1)-βl(H′(ω(k, j-1),μk, j-1))+H(ω(k, j-1),μk, j-1),

其中l(wèi)是使得(ω(k+1, j),μk+1, j)∈Ω0×(0,1]成立的最小正整數(shù),j∶=j+1.

若‖H(ω(k+1, j),μk+1, j)‖≤ε1, 且j≤J1, 則令(ω(k+1),μk+1)=(ω(k+1, j),μk+1, j),hk+1=min{h0,1.25hk}, 轉(zhuǎn)4);

若‖H(ω(k+1, j),μk+1, j)‖>ε1,hk+1=0.75hk,k∶=k+1, 則轉(zhuǎn)3).

4)μk+1≤ε2, 則停; 否則置k=k+1, 轉(zhuǎn)1).

在算法的步驟3)中, (H′(ω,μ))+=H′(ω,μ)T(H′(ω,μ)H′(ω,μ)T)-1是H′(ω,μ)的Moore-Penrose逆.

例1

可行域不滿足偽錐條件, 構(gòu)造動約束函數(shù)如下：

[1] YU Qian, HUANG Chong-chao, WANG Xian-jia. A Combined Homotopy Interior Point Method for the Linear Complementarity Problem [J]. Applied Mathematics and Computation, 2006, 179(2): 696-701.

[2] DING Jun-di, YIN Hong-you. A New Homotopy Method for Nonlinear Complementarity Problems [J]. Numericla Mathematics: A Journal of Chinese Universities (English Series), 2007, 16(2): 155-163.

[3] Song W, Yao G M. Homotopy Method for a General Multiobjective Programming Problem [J]. J Optim Theory Apply, 2008, 138(1): 139-153.

[4] XU Qing, YU Bo, FENG Guo-chen. Homotopy Method for Solving Variational Inequalities in Unbounded Sets [J]. Journal of Global Optimization, 2005, 31(1): 121-131.

[5] LIN Zheng-hua, YU Bo, FENG Guo-chen. A Combined Homotopy Interior Point Method for Convex Nonlinear Programming [J]. Appl Math Comput, 1997, 84(2/3): 193-211.

[6] LIU Qing-huai, YU Bo, FENG Guo-chen. The Homotopy Interior-Point Method for Nonconvex Nonlinear Programming Problem Based on Quasi-normal Cone Condition [J]. Acta Mathematicae Applicatae Sinica, 2003, 26(2): 372-377. (劉慶懷, 于波, 馮果忱. 基于擬法錐條件的非凸非線性規(guī)劃問題的同倫內(nèi)點(diǎn)法 [J]. 應(yīng)用數(shù)學(xué)學(xué)報(bào), 2003, 26(2): 372-377.)

[7] LIN Zheng-hua, LI Yong, YU Bo. A Combined Homotopy Interior Point Method for General Nonlinear Programming Problems [J]. Appl Math Comput, 1996, 80(2/3): 209-226.

[8] SHANG Yu-feng, YU Bo. Boundary Moving Combined Homotopy Method for Nonconvex Nonlinear Programming and Its Convergence [J]. Journal of Jilin University: Science Edition, 2006, 44(3): 357-361. (商玉鳳, 于波. 凸規(guī)劃的動邊界組合同倫方法及其收斂性 [J]. 吉林大學(xué)學(xué)報(bào): 理學(xué)版, 2006, 44(3): 357-361.)

[9] SHANG Yu-feng. Constraint Shifting Combined Homotopy Method for Solving Nonlinear Programming, Equilibrium Programming and Variational Inequality [D]: [Ph D Thesis]. Changchun: Jilin University, 2006. (商玉鳳. 解非線性規(guī)劃、 均衡規(guī)劃和變分不等式問題的動約束組合同倫方法 [D]: [博士學(xué)位論文]. 長春: 吉林大學(xué), 2006.)

[10] Allgor E L, Georg K. Numerical Continuation Method: An Introduction [M]. Berlin: Springer-Verlag, 1990.

[11] Naber G L. Topological Method in Euclidean Space [M]. London: Cambridge University Press, 1980.

[12] FAN Xiao-na, YU Bo. A Smoothing Homotopy Method for Solving Variational Inequalities [J]. Nonlinear Analysis: Theory, Method & Applications, 2009, 70(1): 211-219.