一類積分不等式及其變分計算
王 貝, 雷雨田
(1. 江蘇教育學院 數學系, 南京 210013; 2. 南京師范大學 數學科學學院, 南京 210046)
經典的Hardy-Littlewood-Sobolev(HLS)不等式為[1]
(1)
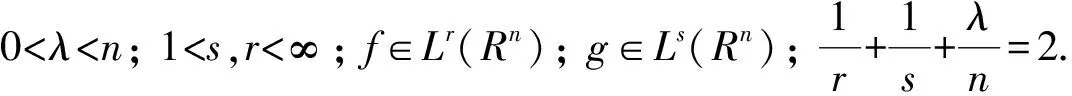
1) 加權HLS不等式[2]:
(2)
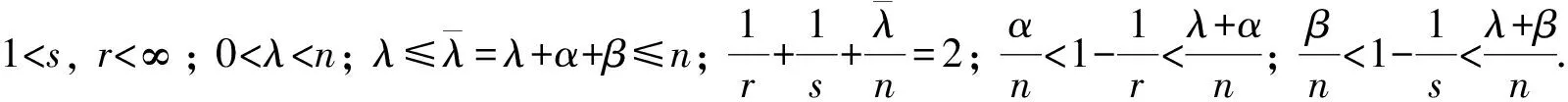
2) Wolff型不等式[3]:
(3)
其中:Wβ,γ(f)是正可積函數f的Wolff位勢:
Iα(f)是f的Riesz位勢:
為研究式(2)的最佳常數, Lieb[4]考慮了泛函
在約束條件‖f‖r=‖g‖s=1下的極大化問題, 并證明了極大元是徑向對稱且單調下降的. 此時, Euler-Lagrange方程組為
(4)
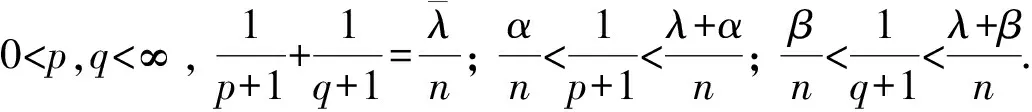
Jin等[5]利用積分形式的移動平面法, 證明了方程組的正解是對稱單調的; 隨后, 他們利用關于正則性的lifting引理, 得到了正解的可積性[6]. 基于此, 文獻[7-9]計算了正解的漸近估計.
特別地, 當α=β=0時, 式(4)退化為HLS不等式最佳常數問題對應的Euler-Lagrange方程組:
(5)

(6)
當α=2時, 式(6)即為Lane-Emden方程組:
(7)
其正解的存在性問題即為Lane-Emden猜想[10].
作為含有Riesz位勢方程組(5)的自然推廣, 考慮含有Wolff位勢的方程組:
(8)
文獻[11-12]分別得到了其正解的可積性和對稱單調性. 在此基礎上, 文獻[13]得到了正解當x→∞時的衰減估計; 文獻[14]將對稱性和衰減估計推廣到多個方程聯立的方程組.
利用文獻[15]的結果及衰減估計可以研究γ-Laplace方程正解的漸近行為[16-17], 利用文獻[18]的結果可以研究k-Hessian方程解的整體性質.
本文結合HLS不等式和Wolff不等式, 給出一種新的Wolff型位勢的積分估計, 并給出了比式(4)更一般的變分結果.
1 積分不等式
定理1設g≥0,g∈Lt(Rn). 記G(x)=Wβ,γ(g)(x), 則G∈Ls(Rn), 且
(9)
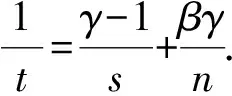
(10)
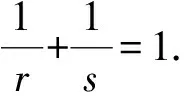
證明: 注意到HLS不等式(1)蘊含
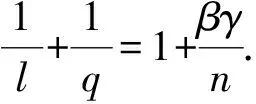
‖Iβγ(g)‖p≤C‖g‖np/(n+pβγ).
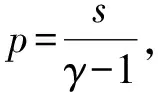
此即式(9).

反之, 利用式(10)可知
證畢.
2 Euler-Lagrange方程
定理2設f,g≥0,f∈Lr(Rn),g∈Ls(Rn). 如果函數K(x,y)>0, 使得如下泛函有意義
且不等式E(f,g)≤C‖f‖r‖g‖s存在最佳常數C*, 則對應的最佳函數f,g滿足:
(11)
經計算, 得
(12)
注意到E(f*,g*)=C*, 式(12)即為
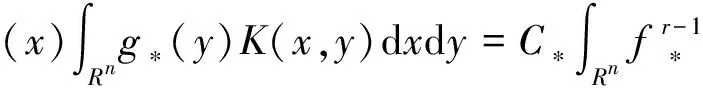
類似地, 可得
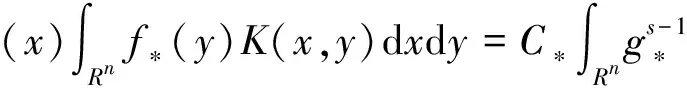
運用變分法基本原理, 可得式(11). 證畢.
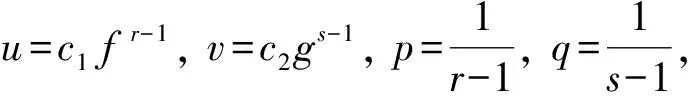
(13)
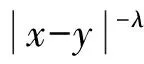
[1] Stein E M. Singular Integrals and Differentiability Properties of Function [M]. Princetion Math Series, Vol.30. Princetion: Princetion University Press, 1970.
[2] Stein E M, Weiss G. Fractional Integrals inn-Dimensional Euclidean Space [J]. J Math Mech, 1958, 7: 503-514.
[3] Hedberg L I, Wolff T. Thin Sets in Nonlinear Potential Theory [J]. Ann Inst Fourier (Grenobel), 1983, 33: 161-187.
[4] Lieb E. Sharp Constants in the Hardy-Littlewood-Sobolev and Related Inequalities [J]. Ann of Math, 1983, 118: 349-374.
[5] JIN Chao, LI Cong-ming. Symmetry of Solutions to Some Systems of Integral Equations [J]. Proc Amer Math Soc, 2006, 134: 1661-1670.
[6] JIN Chao, LI Cong-ming. Qualitative Analysis of Some Systems of Integral Equations [J]. Calc Var Partial Differential Equations, 2006, 26: 447-457.
[7] LI Cong-ming, Lim J. The Singularity Analysis of Solutions to Some Integral Equations [J]. Comm Pure Appl Anal, 2007, 6(2): 453-464.
[8] LEI Yu-tian, MA Chao. Asymptotic Behavior for Solutions of Some Integral Equations [J]. Comm Pure Appl Anal, 2011, 10: 193-207.
[9] LEI Yu-tian, LI Cong-ming, MA Chao. Asymptotic Radial Symmetry and Growth Estimates of Positive Solutions to Weighted Hardy-Littlewood-Sobolev System of Integral Equations [J]. Calculus of Variations and Partial Differential Equations, 2012, 45(1/2): 43-61.
[10] Souplet P. The Proof of the Lane-Emden Conjecture in 4 Space Dimensions [J]. Advances in Mathematics, 2009, 221(5): 1409-1427.
[11] MA Chao, CHEN Wen-xiong, LI Cong-min. Regularity of Solutions for an Integral System of Wolff Type [J]. Advances in Mathematics, 2011, 226(3): 2676-2699.
[12] CHEN Wen-xiong, LI Cong-ming. Radial Symmetry of Solutions for Some Integral Systems of Wolff Type [J]. Discrete Contin Dyn Syst, 2011, 30: 1083-1093.
[13] LEI Yu-tian. Decay Rates for Solutions of an Integral System of Wolff Type [J]. Potential Analysis, 2011, 35(4): 387-402.
[14] LEI Yu-tian, MA Chao. Radial Symmetry and Decay Rates of Positive Solutions of a Wolff Type Integral System [J]. Proc Amer Math Soc, 2012, 140(2): 541-551.
[15] Kilpelaiinen T, Maly J. The Wiener Test and Potential Estimates for Quasilinear Elliptic Equations [J]. Acta Math, 1994, 172(1): 137-161.
[16] LEI Yu-tian, LI Cong-ming, MA Chao. Decay Estimation for Positive Solutions of aγ-Laplace Equation [J]. Discrete Contin Dyn Syst, 2011, 30(2): 547-558.
[17] LEI Yu-tian, LI Cong-ming. Integrability and Asymptotics of Positive Solutions of aγ-Laplace System [J]. J Differential Equations, 2012, 252(3): 2739-2758.
[18] Phuc N, Verbitsky I. Quasilinear and Hessian Equations of Lane-Emden Type [J]. Ann of Math, 2008, 168: 859-914.

