提高ANSYS中BEAM188梁單元計算精度的方法
劉玉卿,陳孝建,楊樹耕,汪 睿,劉小燕
(天津大學,天津300072) ①
提高ANSYS中BEAM188梁單元計算精度的方法
劉玉卿,陳孝建,楊樹耕,汪 睿,劉小燕
(天津大學,天津300072)①
BEAM188單元沿梁長度方向的彎矩為階梯狀分布,與理論分析結果存在較大誤差,對計算精度有很大影響。為提高計算精度,提出了采用二次型的BEAM188單元的方案,并通過計算檢驗了二次型梁單元的收斂速度和計算精度。結果表明,該方案能夠在保證計算效率的前提下顯著地提高計算精度。
海洋平臺;BEAM188;二次型;高斯積分點
在海洋工程中,大型有限元通用軟件ANSYS有著廣泛的應用[1-2]。在海洋平臺上部模塊的板梁組合結構的計算過程中,骨材通常用ANSYS中的BEAM188單元模擬。BEAM188單元在計算時采用默認的設置,此時單元沿梁長方向采用了1個高斯積分點[3],為三維線性單元。
由于線性單元的局限性,計算結果有較大誤差。例如,在計算跨中承受集中載荷的兩端鉸支的單跨梁時,理論上沿梁長方向的彎矩為三角形分布,如圖1所示;而在默認的情況下,BEAM188單元計算得到的彎矩為階梯狀分布,與力學理論值誤差很大,如圖2所示。在彎距分布圖中,與本文計算結果有關的為:MYI和MYJ表示I和J節點的y軸彎矩,MIN和MAX表示最大和最小的彎矩,ELEM表示相應的單元編號。本文僅把彎矩數值列于表中,而不在圖中表示。

圖1 力學模型及力學解

圖2 BEAM188單元彎矩分布圖
在有限元計算中,為了提高計算精度,通常采取細化網格的方法[4]。但是,對于復雜模型,例如海洋平臺的主船體結構,細化網格會直接導致計算量成倍增加,降低計算效率。有時在網格過密時,甚至會導致計算無法進行。
為了在保證計算效率的情況下提高計算精度,本文建議采用二次型的梁單元進行計算,可以有效地提高計算精度。
1 BEAM188單元介紹
BEAM188梁單元是工程計算中常用的單元類型,適合于分析從細長到中等粗短的梁結構。該單元基于鐵木辛哥梁結構理論,并考慮了剪切變形的影響,是三維線性有限應變梁單元[5-6]。
在默認的KEYOPT(3)=0設置時,BEAM188單元為一階鐵木辛哥梁單元,沿著梁長方向采用了1個高斯積分點進行計算,如圖3所示。

圖3 一次型梁單元高斯積分點示意
將BEAM188單元的KEYOPT(3)選項設置為2時,BEAM188為二次型梁單元。二次型單元運用中間節點(中間節點用戶無法修改)提高單元的計算精度。在計算內力時,沿著梁長方向采用兩2個高斯積分點進行計算,得到2個高斯點上的內力,然后將這2個點上的內力進行線性外推,得到單元節點上的節點力,如圖4所示。這種方法能夠精確地計算線性變化的彎距,而且對于非線性變化的彎矩,也要比一次型梁單元的計算精度高。
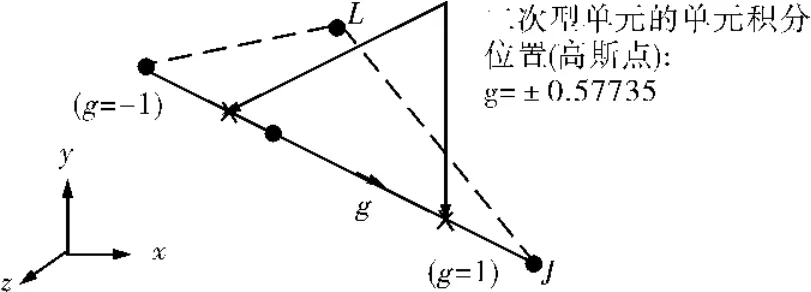
圖4 二次型梁單元高斯積分點示意
2 二次型在單跨梁結構中的應用
前面分別介紹了一次型和二次型的BEAM188梁單元,現在通過簡單的單跨梁結構分析比較兩者在計算精度方面的差異。
建模時,梁截面為T型鋼(300×8+150×12),截面慣性矩為0.384×10-4m4,楊氏模量E=2.0× 108kN/m2,泊松比μ=0.3。
2.1 兩端剛性固定承受集中載荷的單跨梁
承受集中載荷的單跨梁沿梁長方向的彎矩呈線性分布。力學模型如圖5,彎矩分布如圖6~7,計算數據如表1。通過對比一次型和二次型的計算結果可知:
1) 一次型梁單元計算得到的彎矩呈階梯狀分布,與力學理論解有很大誤差。
2) 提高一次型的網格密度,可以提高計算的精確度。
3) 在相同的網格劃分情況下,二次型的計算結果明顯要比一次型的精確。
4) 二次型可以很準確地模擬線性變化的彎矩分布,與理論值無誤差。
5) 二次型的計算精度與網格密度無關,但是將梁的整體作為1個分段的情況除外。

圖5 集中載荷剛固梁力學模型

圖6 集中載荷剛固梁一次型彎矩分布

圖7 集中載荷剛固梁二次型彎矩分布

表1 剛性固定單跨梁在集中載荷作用下的計算結果
2.2 兩端剛性固定承受均布載荷的單跨梁
該力學模型中,沿梁長度方向的彎矩為非線性約束,且彎矩有正也有負,分布于軸線兩側。力學模型如圖8,彎矩分布如圖9~10,計算數據如表2。
對于彎矩為非線性變化的簡支梁結構,通過對比一次型和二次型的計算結果可知:
1) 一次型的彎矩呈階梯狀分布,與力學理論解有很大誤差。
2) 在網格劃分相同的情況下,二次型比一次型更加準確。
3) 提高網格的密度,可以提高計算的精確度,且二次型的計算結果比一次型更快地趨近于理論值。
通過綜合比較BEAM188單元在單跨梁結構計算中的結果可以看出:在收斂速度方面,二次型可以更快地收斂于理論值;在準確度方面,二次型比一次性相對誤差小,尤其在模擬承受集中載荷作用的梁(即彎矩沿軸長方向線性分布)方面,彎矩分布情況和理論解相同,可以得到精確解。
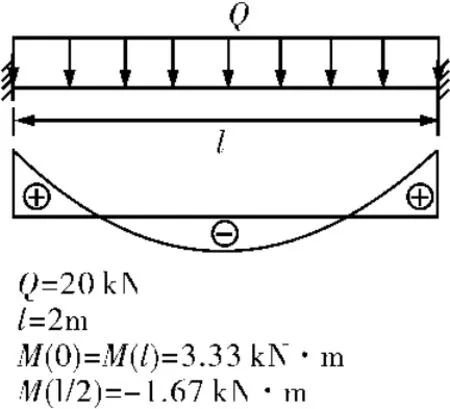
圖8 均布載荷剛固梁力學模型

圖9 均布載荷剛固梁一次型彎矩分布

圖10 均布載荷剛固梁二次型彎矩分布
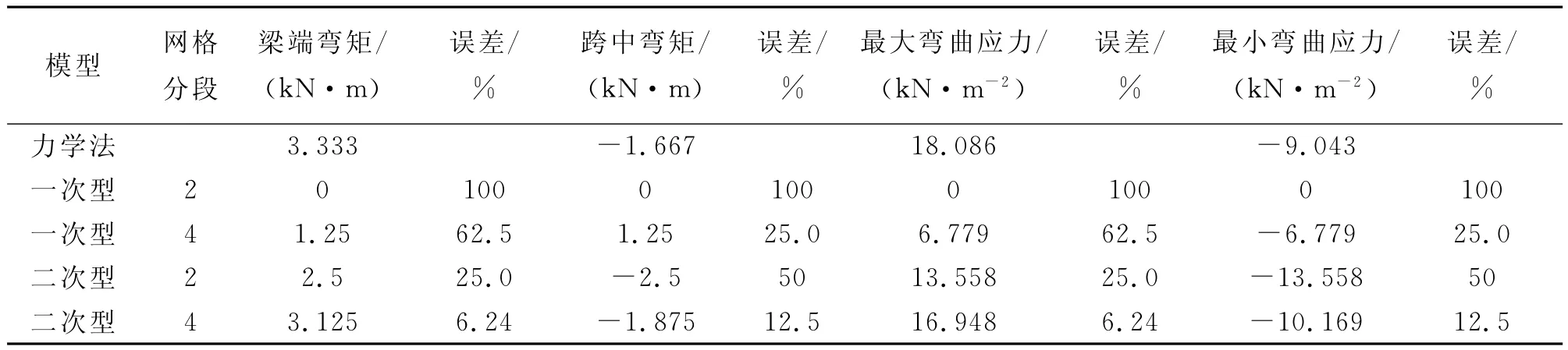
表2 剛性固定單跨梁在均布載荷作用下的計算結果
3 二次型在板梁組合結構中的應用
海洋工程結構物的設計和建造,討論的對象主要是承受垂直于板平面載荷的、具有不同邊界條件的板梁結構,考慮的主要是板和梁的彎曲變形問題。板梁組合結構的模擬計算中,梁(即骨材)通常用BEAM188單元模擬。
前面討論了BEAM188單元在單跨梁結構中的應用,下面比較一次型和二次型的梁單元在板梁組合結構中的精確度。
3.1 四邊自由支撐的板架結構
四邊自由支撐的橫骨架式矩形板架結構如圖11,邊長8m。桁材為T型鋼(600×12+200×18),慣性矩I=0.411×10-3m4;骨材為角鋼(150× 90×9),慣性矩I=0.489×10-5m4;板厚8mm。求均布載荷q=10kN/m2作用下桁材和骨材的彎矩分布(E=2.0×108kN/m2,μ=0.3)。
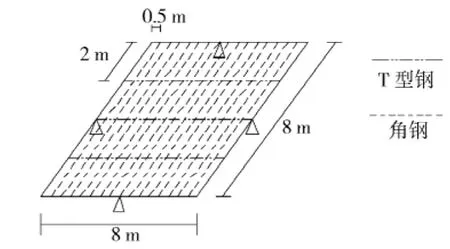
圖11 四邊自由支撐的板架結構
在ANSYS建模時,將桁材和骨材統一設置成一次型或二次型進行求解計算,以分析比較桁材和骨材在一次型或二次型情況下的收斂速度和計算精度。
在建模時不考慮梁單元的偏移,即認為桁材和骨材橫截面的形心在板材的中線面處。
分析得出,板梁組合結構中間位置處的桁材和骨材上的彎矩值相對較大。現在以中間位置處的桁材和骨材上的彎矩分布進行分析比較,如表3~4。
在表3~4中,網格劃分指板格上每一邊的劃分段數。

表3 四邊自由支撐的板架中間位置桁材彎矩計算結果

表4 四邊自由支撐的板架中間位置骨材彎矩計算結果
3.2 四邊剛性固定板架結構
以四周剛性固定的矩形板架為例,分析比較一次型和二次型的計算結果。模型的四周邊界為剛性固定,其余條件均與第3.1節相同,不再贅述。計算結果如表5~6。

表5 四邊剛性固定板架中間位置桁材彎矩計算結果

表6 四邊剛性固定板架中間位置骨材彎矩計算結果
根據有限元原理可知,網格劃分越密集,計算結果越準確[7-9]。由于板架結構不易求得力學精確解,可認為在網格劃分足夠密集的情況下,其結果趨近于精確解,并以其作為精確度的比較判斷標準。
綜合分析以上2種約束情況下的板梁結構的計算數據,可知:
1) 細化網格,可以提高計算精度。
2) 網格劃分越密集,計算結果越精確,但是同時計算量也大。
3) 桁材為板架結構中的強構件,計算結果收斂較快。
4) 骨材的計算結果收斂較慢。
5) 板架結構的計算中,二次型在收斂速度和計算精度方面要明顯優于一次型。
實際的海洋工程結構物,例如主船體的甲板或艙壁板,均為板架組合結構。其邊界條件介于自由支持和剛性固定之間。從以上結果數據的趨勢可以看出,無論是四周自由支持,還是四周剛性固定,二次型在收斂速度和計算精度方面都要優于一次型的BEAM188單元。由此可以推斷,對于介于上述2種邊界條件之間的約束情況,二次型的BEAM188梁單元也要比一次型精確。
3.3 建議
在相同情況下,二次型BEAM188單元的計算精度比一次型高,但是由于計算量大,計算速度比較慢。為了在提高精度的同時保證計算效率,對于復雜結構,建議將重要部位的梁或骨材采用二次型的BEAM188單元模擬,將一般部位的梁構件采用一次型進行模擬,這樣可以在提高計算精度的同時保證計算效率。
4 結論
1) 在有限元計算中,提高網格密度,可以提高計算精度。
2) 在相同的網格劃分情況下,二次型的BEAM188單元在收斂速度和計算精度方面要明顯優于一次型的BEAM188單元。
3) 在結構中綜合運用一次型和二次型的BEAM188單元,可以在保證計算效率的情況下提高計算精度。
4) 本文以單跨梁和板梁結構為例,分析比較了一次型和二次型的BEAM188梁單元在結構計算中的收斂速度和計算精度,并得出了結論。這對提高ANSYS在結構有限元分析計算中的精度和效率具有重大意義。
[1] 楊樹耕,孟昭瑛,任貴永.有限元分析軟件ANSYS在海洋工程中的應用[J].中國海洋平臺,2000,15(2):41-44.
[2] 孫志娟,孟慶鑫,周 到.海洋石油平臺水下夾樁器本體結構分析[J].石油礦場機械,2007,36(1),36-38.
[3] 王勖成.有限單元法[M].北京:清華大學出版社,2003:80-100.
[4] 陳鐵云,陳伯真.船舶結構力學[M].上海:上海交通大學出版社,1991:163-195.
[5] Simo J C,Vu-Quoc L.A Three Dimensional Finite Strain Rod Model.PartⅡ:Computational Aspects[J].Computer Methods in Applied Mechanics and Engineering,1986,58:79-116.
[6] Ibrahimbegovic,Adnan.On Finite Element Implementation of Geometrically Nonlinear Reissner's Beam Theory:Three-dimensional Curved Beam Elements[J].Computer Methods in Applied Mechanics and Engineering 1995,122:11-26.
[7] 江見鯨,何放龍.有限元法及其應用[M].北京:機械工業出版社,2007.
[8] S·鐵木辛哥,J·蓋爾.材料力學[M].胡人禮,譯.北京:科學出版社,1987.
[9] 李 妍,吳艷新,高德利.深水鉆井隔水管縱橫彎曲變形解析[J].石油礦場機械,2011,40(9):21-24.
Study and Improving Accuracy of ANSYS BEAM188Element in Structure Calculation
LIU Yu-qing,CHEN Xiao-jian,YANG Shu-geng,WANG Rui,LIU Xiao-yan
(Tianjin University,Tianjin300072,China)
There is a big error in the bending moment distribution along the beam between the theoretical value and BEAM188element calculation results.In order to improve accuracy,aquadratic BEAM188element is a better choice.The result shows that this method can improve the calculation accuracy in the premise of ensuring computational efficiency.
marine platform;BEAM188;quadratic;Gauss integral point
1001-3482(2012)04-0039-05
TE95
A
2011-10-28
劉玉卿(1986-),男,河北石家莊人,碩士研究生,主要從事船舶與海洋工程結構物的設計與建造工作,E-mail:yqliu_tju@yahoo.com.cn。

