動能桿殺傷增強器殺傷概率計算*
杜安利,王迎春,王 潔,王 琨
(空軍工程大學導彈學院,陜西三原 713800)
0 引言
動能攔截器是指通過高速碰撞直接摧毀目標的飛行器,它屬于反導系統中的高層攔截反導武器。但是由于彈道導彈(TBM)的機動和突防能力不斷增強,雷達在距離探測、跟蹤精度等方面也存在一定的誤差,動能攔截器不可能每次都直接擊中目標,因此在一定的脫靶量下,增強動能攔截器的殺傷能力,已成為人們關注的熱點[1-2]。
動能桿戰斗部技術的出現為研究人員提供了一種新思路。該戰斗部針對破片戰斗部的不足,采用了高密度(采用鎢等重金屬原料)、大質量動能桿作為殺傷增強裝置。這些動能桿群利用動能攔截器和目標導彈之間的相對速度而具有很大殺傷動能,使之能穿透較厚且加固TBM防護層,摧毀導彈,有效提高對目標的殺傷效率[3]。趙英杰等[4]對離散桿類戰斗部的殺傷概率進行了研究,文中針對殺傷增強裝置的動能桿群的殺傷概率進行了研究。
1 動能桿殺傷概率數學模型
1.1 動能桿的分離速度
動能桿的分離速度與炸藥性能、炸藥與動能桿的質量比β(C/M)及戰斗部形狀有關。根據能量守恒定理,經過適當簡化,動能桿的分離速度Vf0可近似表示為[3]:

動能桿的動態初始速度Vfg0為:

式中:Vf0為桿條靜態初始速度矢量;Vm為攔截器的速度矢量。
1.2 有效殺傷半徑
有效殺傷半徑表示了殺傷增強器殺傷威力范圍的大小。由于動能攔截器的制導誤差較小,要求有效半徑也越小,因而殺傷增強裝置也就較輕,戰斗部的有效殺傷半徑Rf可由下式獲得[4-5]:

式中:qf為桿條質量(kg);Cx為桿條的迎風阻力系數;ρ0為海平面的大氣密度(kg·s2/m3);H(Y)為爆炸點高度Y處的相對大氣密度;φa為金屬桿條的形狀系數(m2/kg2/3);g為重力加速度(m/s2);Vfg0為桿條動態初始速度(m/s);EB為桿條擊穿目標必須的最小動能(J)。
1.3 動能桿靜態拋撒時運動規律及有效性判斷
動能桿殺傷增強器在地面靜止狀態下起爆后形成的殺傷環帶(經理論和試驗證明)在擴張中始終垂直于攔截器縱軸,且中心在導彈縱軸上。在空氣阻力的作用下,桿條的運動方程為:

式中:Vf為桿條速度(m/s);Sf為桿條在飛行方向的有效面積(m2);ρ為遭遇點的大氣密度(kg/m3);t為桿條從爆炸時的起飛時間(s)。
為方便起見,引入桿條速度衰減系數:

將桿條t時間內經過的距離r作為自變量時,任意時刻t,桿條靜態的飛散速度可近似表示為:

同理,桿條動態運動時的速度為:

桿條經過距離r后的動能為:

當Ef確定時,如果Ef≥EB(EB為目標殺傷動能),則該桿條為有效殺傷桿條;否則為無效桿條。
1.4 動能桿殺傷增強器的動態殺傷區
殺傷增強器在動態下爆炸,形成桿條的動態飛散區為空心錐,如圖1(a)所示。為推導動態殺傷區的數學表達式,須作以下3個假設:
1)在導彈與目標遭遇時,導彈的速度矢量與目標的速度矢量在同一平面之內;
2)不考慮導彈和目標繞各自重心的轉動對戰斗部和目標要害部位速度矢量的影響;
3)忽略目標的姿態角,即認為目標的速度矢量與其縱軸相重合。
動態殺傷區的主要參數(見圖1(b))為:以動能桿殺傷增強器中心為坐標原點建立彈體坐標系,x軸為殺傷增強器縱軸,相對于目標坐標系而言,桿條的動態速度為Vft,動態運動方向角為φ1I;相對于地面坐標系來說桿條的動態速度為Vfg,運動方向角為φ2I。Vt為目標的運動速度,α為攔截器速度Vm與其縱軸的夾角,γ為彈目交匯角(Vm與Vt的夾角)。

圖1 動態殺傷區及主要參數
將攔截器的速度矢量Vm、目標的速度矢量Vt分別沿x、y軸分解,則有:

由上式可知,殺傷增強器的動態殺傷區取決于彈目遭遇條件和桿條靜態的飛散速度。
1.5 命中目標桿條數的數學期望
命中目標桿條數的數學期望m可表示為:

式中:λ為命中目標的桿條群的面密度(塊/m2);S為目標被動態殺傷區覆蓋的面積(m2)。
在推導λ時,可以近似的認為桿條群在動態殺傷區內沿圓周是均勻分布的如圖2所示。

圖2 殺傷增強器動態殺傷區示意圖

式中:N'f為動態殺傷區內有效桿條總數;Rx是殺傷增強器起爆點坐標X和脫靶量r的函數。為了獲得Rx與r的關系式,首先分析Rx與R'1的關系:

R'1與r的關系如圖3所示,則:


圖3 R'1與r的關系圖
當γ很小時,可以近似的認為 γ≈0°,則 α1≈0°,此時R'1≈r。可見,在尾部攻擊時可以用R'1代替r,而不至于帶來不允許的誤差。將關系式合并,就可以得到λ與X的關系式,這時,λ僅僅是X的函數。
下面推導桿條覆蓋面積S,以圖4為例,顯然,目標被覆蓋的長度L'可表示為:
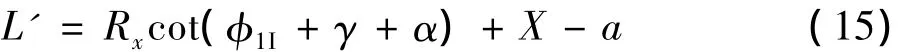

圖4 覆蓋面積計算示意圖
由于目標的半徑都比較大,假設其半徑為R,則殺傷區在目標上覆蓋面的弧長L0為:

實際上,殺傷增強器產生的桿條群并不一定以垂直角度擊中目標,這樣在覆蓋面的兩個邊界處沿桿條飛散方向切割目標的截面不是圓形,而是橢圓。但由于桿條的飛散角一般很小,可近似認為弧長為圓形。則覆蓋面積為:

式中Rx同式(13)。
因此擊中目標桿條數的數學期望為:

1.6 殺傷概率計算
由理論和試驗統計所得到的單個桿條殺傷目標的概率為[3]:

式中:q為桿條質量(g);hc為目標等效硬鋁厚度(mm);h為目標的實際厚度(mm);σb為目標材料的強度極限;σbe為標準硬鋁材料的強度極限。
在這里只考慮單枚桿條擊穿目標的概率,將目標易損段簡化為一圓柱體,不考慮目標的損傷積累,則目標殺傷規律的一般表達式為[3]:

2 算例與仿真計算
在進行仿真計算時,以某動能攔截器攔截某戰術導彈為例,攔截器與目標遭遇點的具體參數為:攔截器的飛行速度2500m/s,目標飛行速度1600m/s,遭遇點高度20000m,彈目交會角為15°。
動能桿殺傷增強器的指標為[6]:殺傷增強器桿條總數 84,平均質量17.83g。

圖5 殺傷概率隨殺傷增強器與目標距離的變化曲線
攔截器殺傷目標的概率與殺傷增強器與目標距離的關系如圖5所示,從圖中可以看出,攔截器的殺傷概率隨殺傷增強器與目標距離的增大而迅速減小,當攔截器與目標之間的距離小于5m時,其殺傷概率可達50%以上,這說明在此范圍內殺傷增強器的殺傷概率最大。由于動能攔截器的制導精度極高(一般為0.15m[7]),因此在滿足殺傷概率要求的同時,可以減輕殺傷增強器的質量,從而減小動能攔截器的總質量,有利于動能攔截器的小型化、輕型化。
3 結論
文中對動能桿殺傷增強器的殺傷概率進行了研究,建立了殺傷增強器的殺傷概率模型。并針對動能桿殺傷增強器的殺傷概率仿真計算,結果表明攔截器的殺傷概率隨殺傷增強器與目標距離的增大而迅速減小,當攔截器與目標之間的距離小于5m時,其殺傷概率可達50%以上。文中的結果可為動能攔截器的效能分析提供參考。
[1]Luis A Espino.Computer modeling for damage assessment of KE-Rod warheads against ballistic missiles[D].Graduate School of the University of Texas at El-Paso.July 2004.
[2]王迎春,王潔,杜安利.桿式戰斗部在動能攔截器殺傷增強裝置中的應用[J].飛航導彈,2010(6):87-90.
[3]丁建超,王朝志,陳萬春.反TBM導彈動能桿戰斗部優化設計[J].戰術導彈技術,2005(4):7-11.
[4]趙英杰,景航,黃長強.離散桿式戰斗部類導彈殺傷概率研究[J].彈箭與制導學報,2003,23(2):37-42.
[5]李廷杰.導彈武器系統的效能及其分析[M].北京:國防工業出版社,2000.
[6]萬軍.動能桿類戰斗部殺傷元素爆炸驅動的數值模擬研究[D].長沙:國防科技大學,2003.
[7]王正青.動能殺傷器技術的發展及應用前景[J].地面防空武器,2005(5):6-14.

