用Excel進行威布爾型產品可靠性數值仿真評估

張仕念，張國彬，易當祥，顏詩源，楊艷妮

（北京市清河大樓子八，北京 100085）

0 引言

可靠性仿真是將仿真技術應用于可靠性分析的一種方法，利用計算機技術對己經建好的系統可靠性模型進行仿真，得到一系列的仿真結果，能夠解決常規的解析法很難奏效的部分可靠性問題。可靠性仿真具有經濟性好、應用范圍廣、通用性好、難度小、直觀和保密等優點[1]。Microsoft Excel是微軟公司開發的電子表格軟件，易學易用，使用范圍廣；Excel 2003就提供了財務、日期與時間、數學與三角函數、統計等九大類約300個函數，具有強大的計算、統計功能。本文以服從威布爾分布的數據為例，利用Excel的、已有函數和單元格的引用，進行復雜的數值計算，利用RAND（）函數產生的隨機數而引入隨機因素，實現可靠性評估的數值仿真。實例表明，用Excel進行可靠性評估的數字仿真，可以避免繁雜的編程工作，省時省力，方便實用，且仿真結果與計算結果十分接近。

1 威布爾型數據的可靠性評估模型

設n臺產品進行無替換截尾試驗，失效時間為t1≤t2≤…≤tr（r≤n）， 定數截尾時 tr為第 r個產品的失效時間，定時截尾時tr為截尾時間，失效數據服從兩參數威布爾分布。其密度函數為：

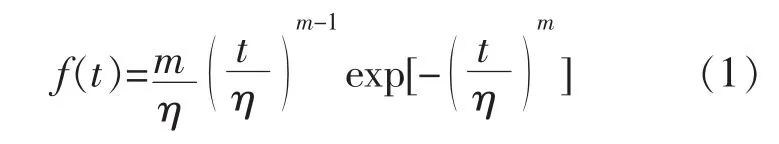
分布函數為：

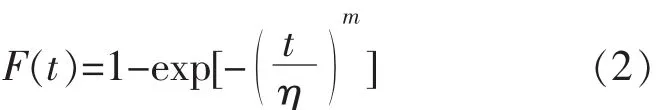
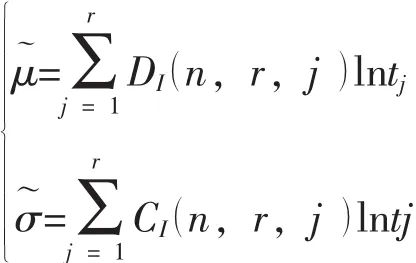
式中， DI（n， r， j ）， CI（n， r， j）可查 《可靠性試驗用表》[3]獲得。

對給定的n，r，γ，R，Mann等給出了樞軸量：

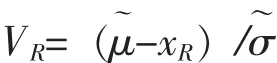
的γ分位數VR，γ數表，式中xR是極值分布的 （1-R）分位數，即

2 威布爾型數據的可靠性數字仿真

則tR的置信下限：

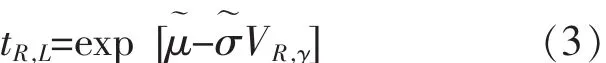
根據對稱原理， 在式 （3） 中將tR，L→t0，R→RL（t0）， 得可靠性下限 RL（t0） 的表達式為：

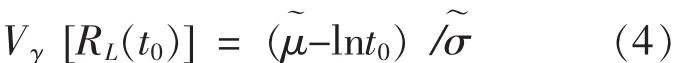
故可反查Vγ（R）-R表，用中轉查值法可求出 RL（t）。

2.1 隨機數的產生及隨機變量抽樣

目前，廣泛應用的、在 [0，1]上產生均勻分布的偽隨機數的方法是同余法[3]，包括混合同余發生器、乘法同余發生器等。Excel提供的RAND（）函數也能夠產生 [0，1]的隨機數，在其幫助中，說明該函數用于 “返回大于等于0及小于1的均勻分布隨機數，每次計算工作表時都將返回一個新的數值”。用RAND（）函數產生5次，每次5組， 每組 5000個隨機數，用 Co（i，j） （i≠j）表示第i組和j組隨機數的相關系數，隨機數之間的相關系數見表1。由表1可見，其相關系數很小，表明各組隨機數之間的獨立性很好。本文用RAND（）函數產生隨機數。

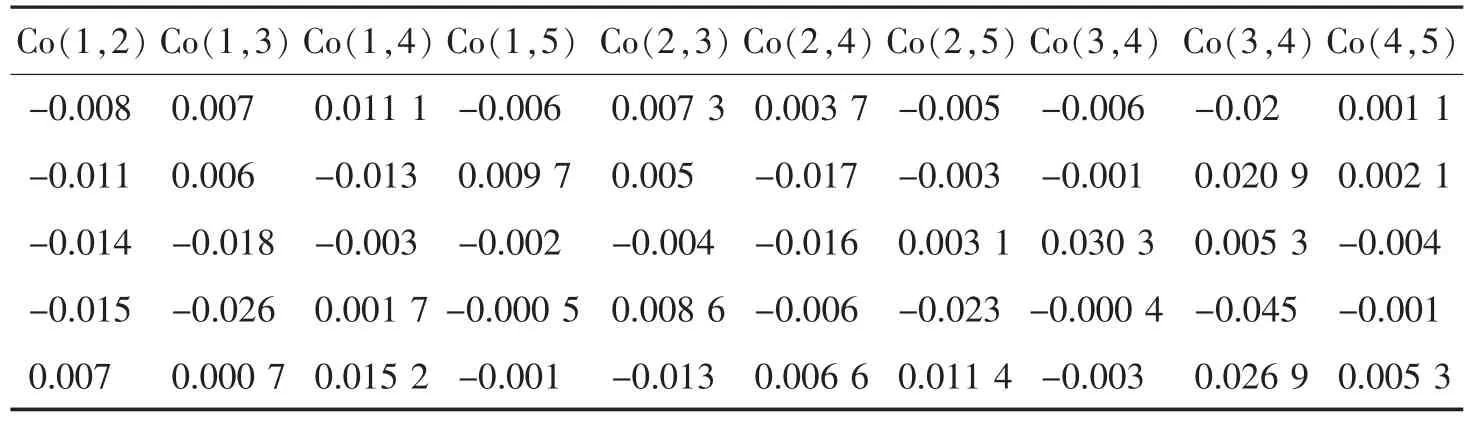
表1 5組隨機數的相關系數

可采用逆變法[4]產生服從威布爾分布的隨機數，具體的步驟如下：

a）在 （0，1）區間上產生服從均勻分布的隨機數 r。

b）做變換。

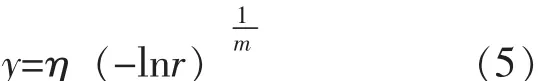
式 （5）中：y——服從參數為m，η的威布爾分布的隨機數。

c）重復步驟a）、b），直到取到要求數量的隨機數為止。

2.2 分布參數的最小二乘估計

由式（2） 得：

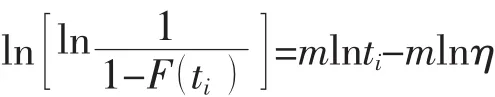
令

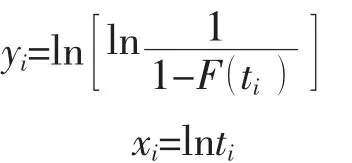
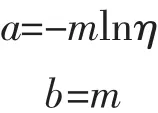
則

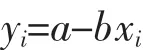
如果ti服從威布爾分布， {xi，yi}成線性關系，通過最小二乘法線性回歸，解得系數a、b。

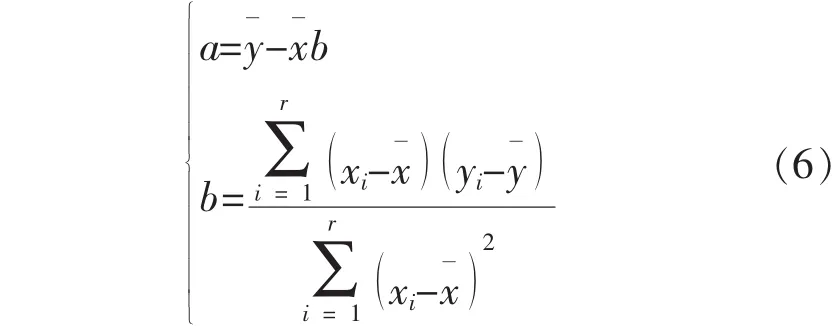
則

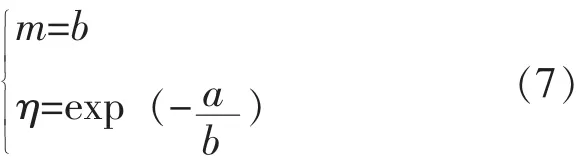
兩個變量的相關系數表示為：

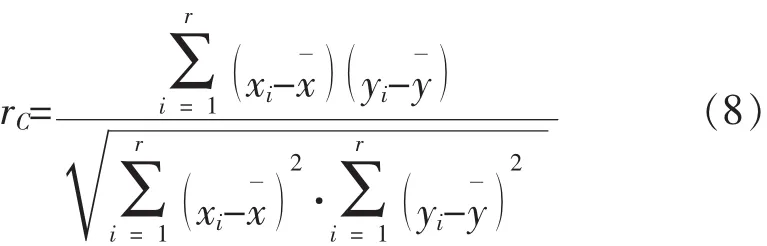
可根據|rC|→1的程度，判斷是否服從威布爾分布。

在計算過程中，無替換定數截尾時，分布函數為：

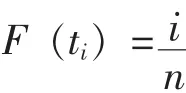
小樣本 （n≤20）時，為了減少計算誤差，用下式計算：

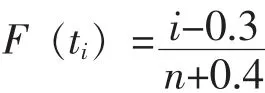
2.3 仿真步驟

數字仿真的基本思路是：用最小二乘法根據原始數據估計分布參數和，利用隨機數發生器和逆變法抽取服從分布參數為和的威布爾分布的抽樣樣本，根據抽樣樣本計算出可靠度的一個抽樣值，反復抽樣，得到可靠度的分布密度函數，從而獲得可靠度的置信下限。具體的步驟如下：

a）根據最小二乘法，利用Excel軟件的單元格 引 用 和 LN （number）、 AVERAGE （number1，number2， ...）、 EXP （number） 等函數， 由式 （6）和 （7） 計算威布爾分布的分布參數m^和η^。

b）從仿真循環次數i=1開始，由式 （5），在Excel軟件電子表格的某一列用 “=*POWER （（-LN （RAND （））），” 產生 r個服從威布爾分布的隨機數；在另一列用 “=SMALL（array1，k）”（array1為r個隨機數組成的數列，k=1，2，…，r）函數對其由小到大排序，得故障產品的抽樣觀察值為ti1，ti2，…，tir（無替換定時截尾時，產生n個服從威布爾分布的隨機數，取定時截尾時間T0以前的樣本排序）。

c）由故障產品壽命的抽樣觀察值ti1，ti2，…，tir，同a），采用最小二乘法估計抽樣樣本的分布參數為和。

d）對于給定任務時間t0，對應的可靠度抽樣值為：

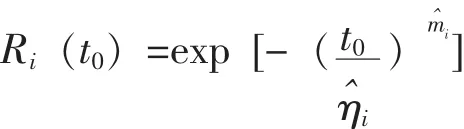
e）i=i+1重復上述過程，1≤i≤N，N為仿真次數。單元格引用和公式在Excel電子表格中建立后，只需做簡單的拷貝即可完成。

f）給定置信度γ，在可靠度的分布密度函數中， （1-γ）N的整數部分對應的Ri（t0）， 就是給定置信度為γ的可靠度下限值，即在某一單元格用 “=SMALL （array2，（1-γ）*N）” 的返回值即為仿真結果，此處的array2為仿真結果組成的數列。

給定可靠度R的可靠壽命tR的抽樣公式為：

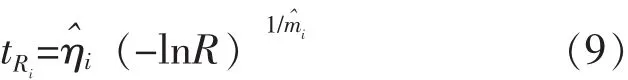
對tRi反復抽樣，進行排序得tR1≤tR2≤…≤tRN，對于給定的置信度γ的壽命下限tR為 （1-γ）N的整數部分對應的tRi。

4 仿真算例

取某產品15臺進行無替換定數截尾自然貯存試驗，10臺產品出現失效，失效時間分別為 （單位 ： 年 ） ：14.71、 15.09、 18.29、 19.91、 20.67、21.87、 22.32、 22.87、 24.91、 25.06。 給定置信度為0.75，求：a）給定可靠度R=0.95時產品的可靠壽命下限；b）任務時間t0=14年時的產品貯存可靠度下限。

采用最小二乘法估計以上數據的參數時，用式 （8）計算相關系數rC=0.977638，可以認為該產品的貯存壽命服從威布爾分布。查 《可靠性試驗用表》獲得n=15、 r=10 時的 DI（n， r， j）、 CI（n， r，j）。

現用Excel對其進行仿真，每次抽取4000個樣本，仿真5次所得的結果見表2。由表2可見，5次仿真的可靠壽命的平均值為12.053，計算值為12.43，5次仿真的貯存可靠度的平均值為0.920，計算值為0.919，二者很接近。

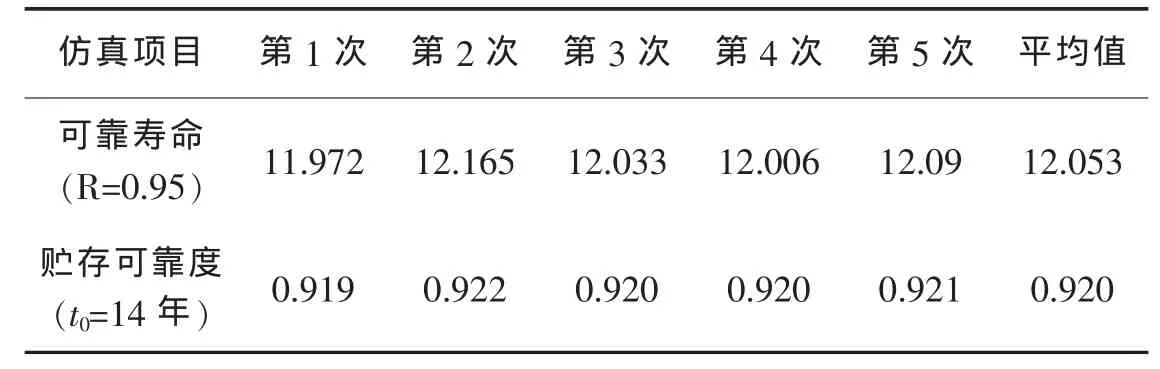
表2 某產品的可靠壽命、可靠度仿真結果

4 結束語

通過以上分析和實例可以看到，采用Excel進行可靠性數值仿真，只需利用Excel提供的函數和單元格的引用就可實現復雜的數值計算，簡單直觀，方便實用，仿真結果準確可信，對可靠性評估研究和可靠性分析計算具有重要的參考價值，有助于可靠性仿真技術的推廣應用。

[1]陸勝勇.可靠性仿真技術 [J].電子產品可靠性與環境試驗， 1999， （1）： 19-22.

[2]周源泉.質量可靠性增長與評定方法 [M].北京：北京航空航天大學出版社，1997.

[3]中國電子技術標準化研究所.可靠性試驗用表[M].增訂本.北京：國防工業出版社，1987.

[4]宋筆鋒.飛行器可靠性工程[M].西安：西北工業大學出版社，2006.