Matlab輔助高等數學教學方法初探

夏靜 卜華龍

（1 巢湖學院數學系，安徽 巢湖 238000）

（2 巢湖學院計算機與信息工程學院，安徽 巢湖 238000）

1 引言

高等數學是高校絕大部分理工科專業必修的一門基礎理論課，高等數學有其固有的特點，即高度的抽象性、嚴密的邏輯性和廣泛的應用性。傳統的數學教學方式往往是一支粉筆，一塊黑板以及對問題的靜態描述，難以幫助學生深入淺出的理解教學內容，可能導致一部分學生失去學習興趣和信心，從而難以取得預期的教學效果[1,2]。

提高學生興趣、幫助學生理解抽象內容一直是困擾教師的難題，隨著計算機與數學軟件的發展，適當利用這類工具能改善這一問題[3,4]。Matlab是矩陣實驗室（Matrix Laboratory）的簡稱，是美國MathWorks公司開發的一種數學軟件，可用于算法開發、數據可視化、數據分析以及數值計算的高級技術計算語言和交互式環境。本文通過教學中一些典型問題為例，探討Matlab在高等數學教學中的使用。

2 MATLAB圖形輸出功能的應用

教學時，為使學生直觀理解高等數學問題，我們往往會借助幾何圖形講解，然而，手工作圖不準確，尤其是多維空間圖形，手工示意圖更是差強人意。借助MATLAB軟件功能，我們通過調用MATLAB命令，就可以準確畫出所需圖形，從而降低教與學的難度，提高學生學習興趣，并培養學生通過數學軟件解決數學問題的意識和能力。

2.1 深化對極限的理解

極限是高等數學里的第一個重要的抽象概念，實際上，中學的數學課程里已經有一些簡單的極限知識，學生往往認為只要會進行一些具體極限的計算就可以了，但若不能很好理解極限的數學定義，將對后續知識的學習產生極大的影響，比如函數連續，可導等重要概念都是建立在極限的基礎之上的。若在講解定義過程中展示出極限的“無限靠近”特征，通過幾何圖形則能夠很好地體現其內涵，可使學生理解得更加深刻，教學效果明顯提高。

在MATLAB的命令窗口中輸入如下命令集合：

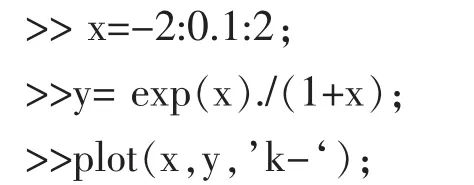
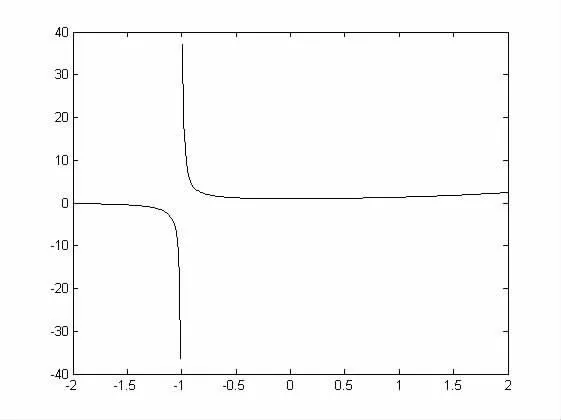
圖1 極限示意圖

2.2 觀察函數級數展開后的逼近程度

以函數的Taylor冪級數展開為例:

若在x=a點附近進行Taylor冪級數展開，則得出：

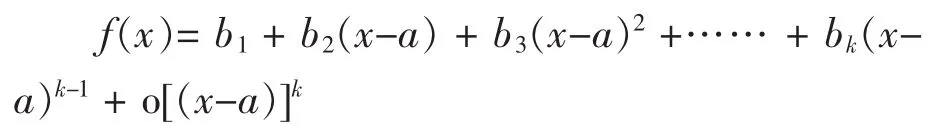
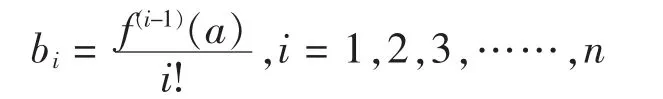
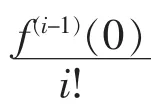
例2 對余弦函數Taylor冪級數方式展開，并觀察不同階次的擬合程度。

在MATLAB的命令窗口中輸入如下命令集

特別的，當函數在x=0點附近進行Taylor冪級數展開，則得出

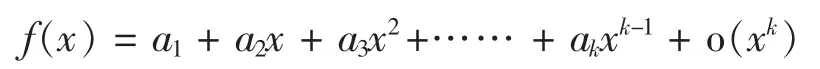
其中，每個系數ai的確定方法與前面一樣，

ai＝合:

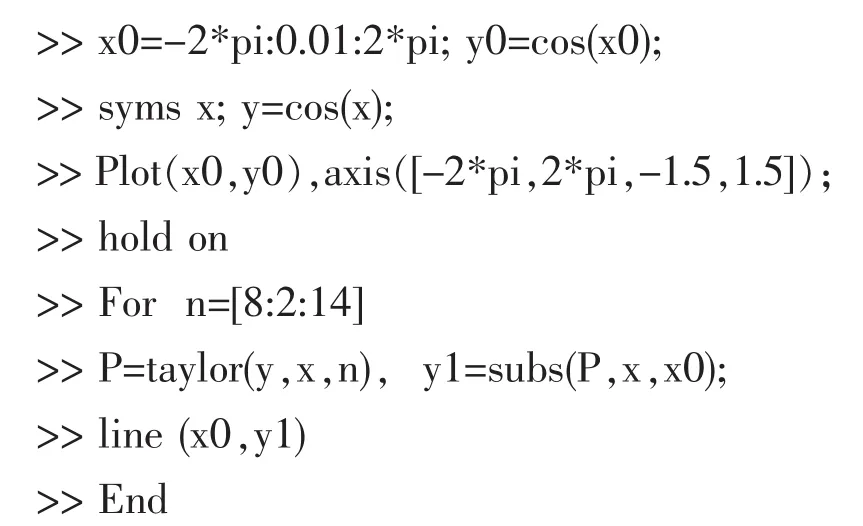
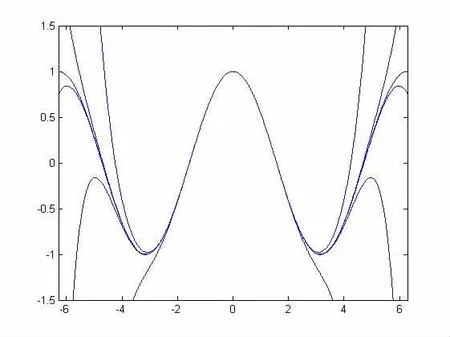
圖2 各階余弦函數擬合曲線

上圖2得到了余弦函數各階次的擬合曲線，從圖中可以發現，若擬合次數低，則擬合效果較好的范圍較小，若增加擬合的階次，則擬合程度好的范圍將顯著增加。

2.3 幫助學生學習空間解析幾何

對于傳統的高等數學里的空間解析幾何部分教學，學生普遍感覺學習吃力，原因是難以想象復雜空間圖形，更難以作圖。若能正確做出圖形，學生若“真實”的看見圖形，則能極大程度上提高學生理解深度，也就是說圖形的有無是能否解決問題的決定性因素之一。

例3 試繪制出二元函數z=x2+y2+5的圖像。

在MATLAB命令窗口輸入如下命令集合：

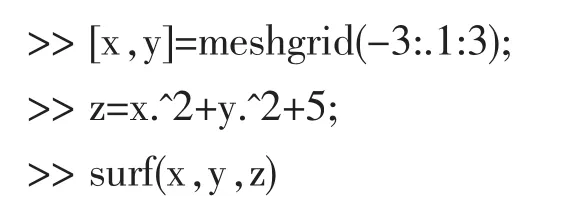
結果圖如下圖3：

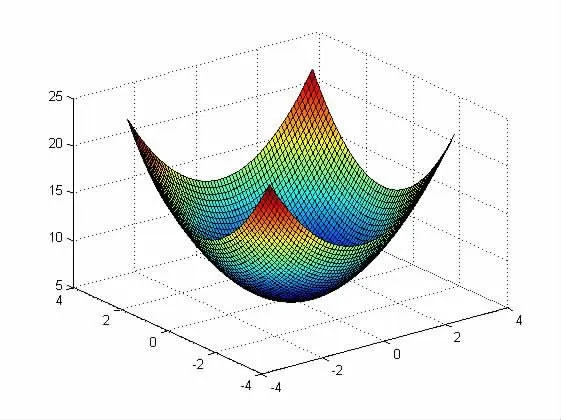
圖3 二元函數示意圖

3 Matlab強大的數值處理功能的應用

不少高等數學問題理論簡單但計算量大，學生在解決這類問題時往往花費很多時間計算，卻得不出正確結果，這導致部分學生對這類數學問題“望而卻步”，降低學生學習興趣。應用Matlab相關命令，就能輕松解決繁雜的計算。

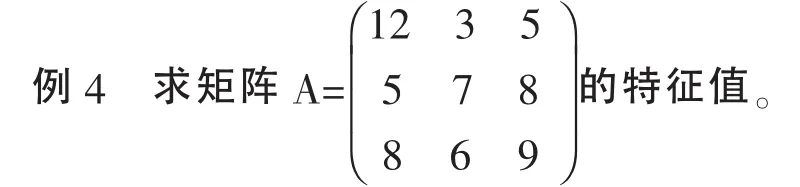
求A矩陣特征值可以直接調用MATLAB中的 eig（）函數。

在命令窗口輸入：

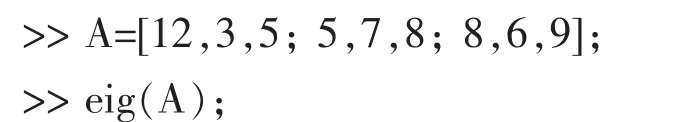
從而立刻得到矩陣A的特征值如下：

由上可見，繁雜的計算在Matlab里只需一條簡單的命令就能解決，這有助于激發學生學習數學方法和數學工具的興趣，提高學生解決數學問題的能力，將數學的工具性作用落到實處。

4 總結和展望

除了以上列舉的一些典型應用，Matlab還可以深入高等數學的很多方面。通過MATLAB形象化、具體化各類抽象問題、簡單化繁瑣的計算，可以提高學生學習興趣，也能增強學生編程動手能力。既有益于高等數學教學，也有益于編程能力的開發。當前的高校各類課程教學，對教師提出了更高要求，結合各類新興的教學工具和教學軟件提高教學效果，不失為高等數學教學的一條新思路。

[1]薛定宇，陳陽泉.高等應用數學問題的MATLAB求解[M].北京：清華大學出版社，2004.

[2]郭志軍.論高等數學中計算的 MATLAB 實現[J].中州大學學報，2007，24（4）：116-118.

[3]張愛華，付宏偉.MATLAB在高等數學教學中的應用研究[J].軟件導報，2008，7（6）：161-163.

[4]趙亞男，牛嚴濤.MATLAB在解析幾何教學中的應用[J].長春大學學報，2011，21（4）：54-58.