統計方法校正O3LYP方法計算的生成熱

王秀軍 龍 汨

(華南理工大學化學與化工學院,廣東省燃料電池技術重點實驗室,廣州510640)

統計方法校正O3LYP方法計算的生成熱

王秀軍*龍 汨

(華南理工大學化學與化工學院,廣東省燃料電池技術重點實驗室,廣州510640)

由于引入各種內在近似,密度泛函理論存在固有誤差.本文采用O3LYP/6-311+G(3df,2p)//O3LYP/ 6-31G(d)計算了220個中小型有機分子的生成熱(ΔfH?calc),隨后應用神經網絡(ANN)和多元線性回歸(MLR)方法對ΔfH?calc進行校正.采用計算得到的生成熱、零點能、分子中原子總數、氫原子個數、雙中心成鍵電子數、雙中心反鍵電子數、單中心價層孤對電子數、單中心內層電子數作為ANN和MLR的描述符.以180個分子作為訓練集構造ANN或MLR模型,并對40個獨立測試集分子的ΔfH?calc進行了預測.結果表明:經過ANN和MLR校正后,訓練集分子生成熱的理論計算值和實驗值間的均方根偏差(RMSD)從24.7 kJ·mol-1分別降低到11.8、13.0 kJ· mol-1;獨立測試集分子的RMSD從21.3 kJ·mol-1分別降低到10.4、12.1 kJ·mol-1.因此ANN模型的擬合和預測能力要明顯優于MLR模型.

O3LYP;神經網絡;多元線性回歸;生成熱;均方根偏差

1 引言

分子的能量是分子最基本的物理量.在實際研究中無法測定體系精確的能量,因此我們更關心那些能夠表征體系能量的熱力學函數,其中生成熱(ΔfH?)就是一個最基本的表征化合物在標準狀態下穩定性的熱力學量,對判斷有機反應的方向和限度也十分重要,并且實驗上可以測得其精確值,1-3因此生成熱的應用十分廣泛.但是實驗上要精確測定一個化合物的生成熱也是很困難的,不僅需要一套合適的裝置,還需要花費大量的時間,并且還需要測定者有很豐富的測定經驗,而且不同的計算方法間也會有偏差,4-6有時新測定的結果還會否定舊的實驗結果,7因此近年測定新的化合物生成熱數據的報導很少,于是發展一個簡單的并能準確預測生成熱的計算模型是非常必要的.

隨著計算機技術的飛速發展,科學工作者對計算化學越來越依賴,從而計算化學已成為對實驗結果的解釋和預測不可缺少的工具.8與經典從頭算方法相比,密度泛函理論(DFT)具有計算花費少,而且可以計算更大的分子,它在計算量子化學領域廣泛應用,已經成為化學、凝聚態物理、材料科學和分子生物學中重要的研究工具,但是DFT計算仍然存在一些計算偏差.例如目前最流行的雜化密度泛函B3LYP計算存在一些缺陷:隨著系統增大偏差增大;9,10它所計算鍵的離解焓偏低;11,12得到不準確的異構體能量差別;12低估了反應能壘;13,14不能準確計算分子間的范德華作用力.15Cohen和Handy16在B3LYP的基礎上發展了一種新的泛函—O3LYP,他們引入一個交換泛函OPTX.近幾年的研究發現O3LYP的計算結果要優于B3LYP.17-23

雖然Gn(n=1-4)方法在計算小分子生成熱方面成效非常顯著,9,24-29但是它們的計算花費不經濟,科學家一般不利用此類方法計算大分子的生成熱.另一方面,由于DFT計算的一些固有偏差,其局限性也越來越突出,尤其是在計算大分子體系時更是如此.因此,一些學者提出了一些校正模型對DFT計算結果進行校正,并取得了令人滿意的結果. Chen等30,31首次采用ANN校正了密度泛函理論的計算結果,生成熱的計算值與實驗值之間的均方根偏差從89.5 kJ·mol-1(或50.2 kJ·mol-1)降為13.0 kJ· mol-1(或13.8 kJ·mol-1).Fan等32提出了用自然鍵軌道(NBO)分析并運用神經網絡校正350個分子的計算生成熱,減少了350個分子的生成熱的計算偏差,隨后他們運用多元線性回歸算法校正DFT計算的生成熱,也成功地減小了DFT的計算偏差.33Li等34利用支持向量機模型也成功地校正了DFT計算的生成熱.這說明神經網絡,多元線性回歸,支持向量機等統計方法是適合于校正DFT計算結果的. Chen35及本課題組36也采用神經網絡模型通過調節B3LYP雜化密度泛函中三個參數來減少密度泛函理論計算的分子熱力學性質數值同實驗值的偏差,并取得了成功.本文利用ANN和MLR的方法來校正O3LYP計算的220個有機分子的生成熱,并對這兩種校正方法的計算結果進行比較.

2 方法理論

2.1 計算方法

本文選用的是包括小型(重原子數目＜6)和中型(重原子數目≥6)的220個有機分子,所有的分子都是由H、C、N、O、F、S、Cl、Br這幾種原子組成,每個分子中含有1-12個C原子,這些分子的生成熱實驗值都是從實驗手冊中獲得.1-3所有分子在這三本手冊中的ΔfH?的實驗值偏差都小于4 kJ·mol-1.30在上述分子中,選取文獻30中的180個分子作為訓練集用于構造ANN或MLR模型,利用交叉驗證的方法來檢驗ANN和MLR的校正結果.本文首先用O3LYP/ 6-31G(d)方法優化所有分子的結構,然后用O3LYP/ 6-311+G(3df,2p)方法計算其生成熱,作為訓練集的180個分子和測試集的40個分子計算結果與實驗值的RMS偏差分別是24.7、21.3 kJ·mol-1.對所有分子進行了NBO分析.NBO分析得到的分子的結構參數用于構造ANN(MLR)模型的描述符(自變量).所有O3LYP計算均采用Gaussian 09程序包.37

在構造統計校正模型時,最重要的一點就是關于分子的物理描述符的選擇,因為這些描述符被用作神經網絡的輸入層和多元線性回歸的自變量.首先我們選擇O3LYP計算的生成熱()作為統計模型的第一個描述符.Chen等30在利用神經網絡改進B3LYP計算的時,他們發現對神經網絡的校正結果非常顯著,因此可以作為第一個描述符.另外Gn(n=1-4)在計算中小型分子生成熱時效果顯著,這是因為在Gn方法中引入了一個高階校正(HLC)項來抵消一系列計算后剩余能量偏差,26而HLC主要采用了分子和原子中的價層孤對電子和未成對電子對其能量進行最后擬合得到.Gn方法認為大部分的相關能是由占據在同一個分子軌道上的電子之間的相互作用引起的,因此電子越多,它們的相關能就越大,且成對電子對相關能的貢獻和未成對電子是不一樣的.而且G4對原子和分子采用不同的參數,說明電子在分子環境和原子環境中,它們對相關能的貢獻也不一樣.鑒于以上分析,本文也采用NBO計算分子的雙中心成鍵電子數(BD)、雙中心反鍵電子數(BD*)、單中心價層孤對電子數(LP)、單中心的內層電子數(CR)這四個參數作為描述符.考慮到分子的大小對的計算偏差有很大的影響,其偏差隨著原子數的增加而遞增,因而把原子總數(NT)和氫原子個數(NH)作為描述符.分子的零點能(ZPE)是計算的一個重要參數,因此將ZPE作為另一個重要的描述符.30

2.2 多元線性回歸模型

采用SPSS11.01統計軟件分析180個分子訓練集的上述描述符參數與生成熱實驗值的關聯度,并構建實驗值的多元線性回歸方程如下:

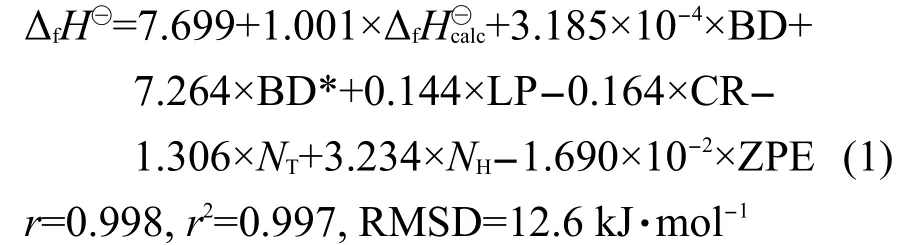
其中,ΔfH?為應用MLR方程校正后的生成熱值,r為相關系數,RMSD為均方根偏差.

2.3 神經網絡模型

神經網絡是一個由許多簡單的并行工作的處理單元組成的系統,其功能取決于網絡的結構、連接強度以及各單元的處理方式.所采用的神經網絡模型包含有輸入層,隱藏層和輸出層三層.本文中的神經網絡結構見圖1,其中輸入層(X1,X2,X3,…)是由8個描述符和一個偏置量(bias)組成,隱藏層包含有3個隱藏神經元(y1,y2,y3),一個輸出層是輸出校正后的分子生成熱.{Wxij}和{Wyj}表示突觸權重,其中{Wxij}是連接輸入神經元和隱藏神經元的突觸權重,{Wyj}是連接隱藏神經元和輸出神經元的突觸權重.在神經網絡模型中所用的轉換函數是sigmoid函數.輸出層Z與輸入層Xi的關系由公式(2)和(3)描述:

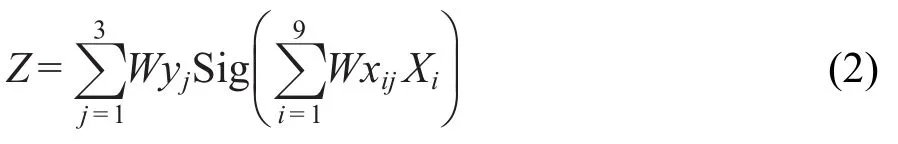
其中,

這里Z為經ANN校正后的生成熱值,Xi對應圖1中給出的8個描述符和一個偏置量,Sig(v)為sigmoid函數.

2.4 模型的驗證

本文采用六重交叉驗證的方法來驗證MLR和ANN模型的校正結果,即將180個分子分成兩組,其中一組共有150個分子作為訓練集,另一組30個分子作為測試集,這個過程循環重復了6次.同時計算評價模型擬合能力的標準回歸系數(q2)和RMSD. Tropsha等38將q2定義為:

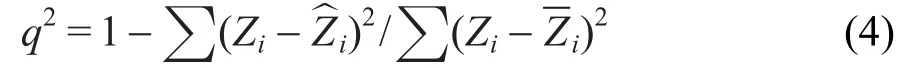
其中,Zi和分別表示物種的實驗值和預測值,Zi表示物種訓練值的平均值,因此本文采用的計算公式如下:

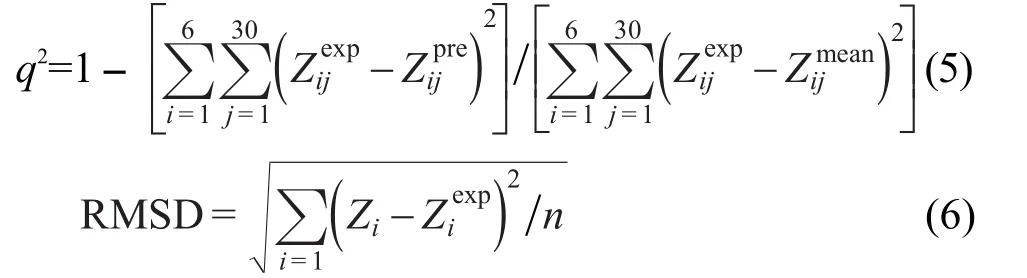
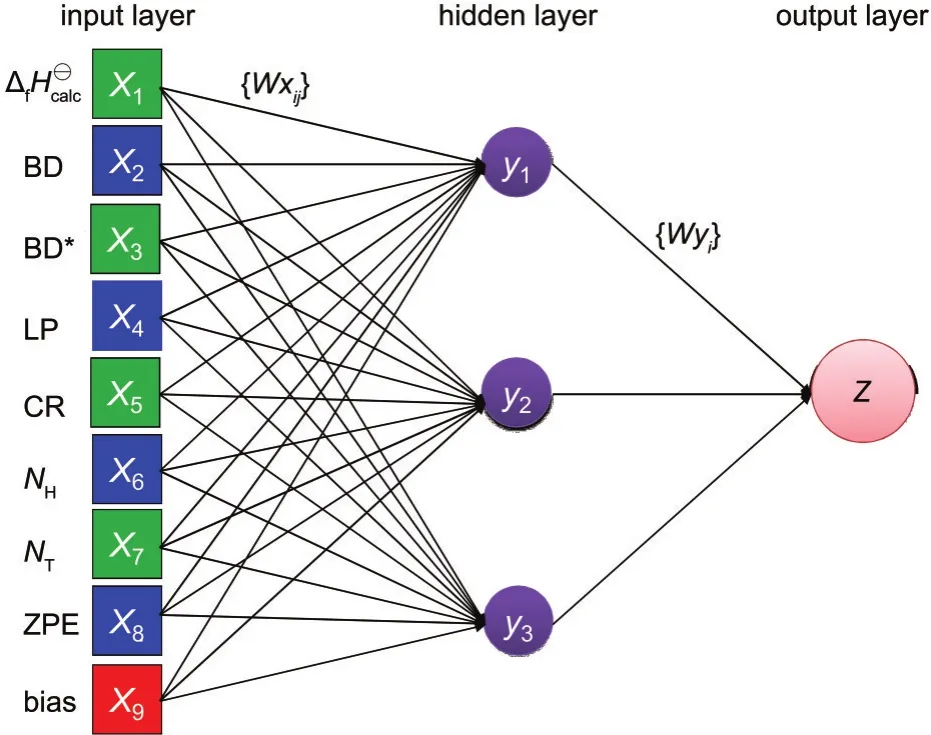
圖1 神經網絡的結構Fig.1 Structure of the neural networkXi(i=1-9)are ΔfH?calc,the total quantities of atoms(NT),hydrogen atoms(NH),2-center bond(BD),2-center antibond(BD*),1-center valence lone pair(LP),and 1-center core pair(CR),the zero point energy(ZPE)and bias,respectively.yj(j=1-3)are the number of hidden neuron.{Wxij}are the synaptic weights connecting the input layer(Xi)and the hidden neurons(yj)and{Wyj}connect the hidden neurons and the output(Z).Z is the ΔfH?corrected byANN.

3 結果與討論

3.1 MLR校正生成熱

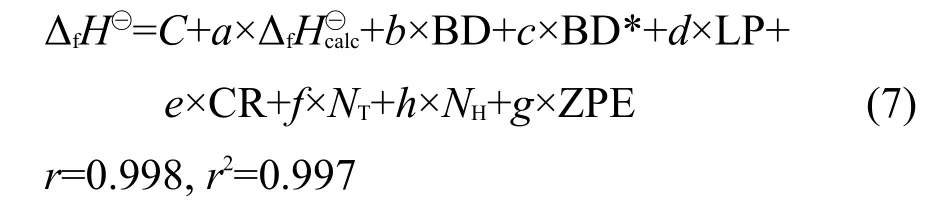
其中,系數a-g對每次回歸分析都有不同的數值,與方程(1)相比,經過交叉驗證后得到的r與r2幾乎不變,MLR的結果分析見表1.由表1可知,MLR經交叉驗證后的q2值是-0.53,訓練集的平均RMSD是12.5 kJ·mol-1,但是測試集的平均RMSD高達15.1 kJ·mol-1,總體RMSD是13.0 kJ·mol-1.Cramer等39曾指出q2為負值是因為測試集的平均偏差要大于訓練集的平均偏差,說明模型預測能力較差.Golbraikh和Tropsha40曾提出統計參數q2＞0.5,r2＞0.6的模型有效,同時Tropsha等也認為模型的預測能力比擬合能力更為重要,即q2的大小更為關鍵.由上述實驗結果可知,利用MLR來預測中小型分子的生成熱是不可靠的.MLR雖然在訓練集中可以降低生成熱的RMSD,但是其模型的預測能力較差.

3.2 神經網絡校正生成熱

圖2是O3LYP計算結果、MLR校正結果(O3LYP-MLR)、ANN校正結果(O3LYP-ANN)和實驗值的對比以及偏差直方圖.由圖2(a,b)可知,與實驗值相比,原始的O3LYP計算結果存在很大的系統偏差,偏差在±4 kJ·mol-1范圍內的分子個數只有24個,經過神經網絡校正后(見圖2(e,f)),生成熱的校正結果明顯更加接近于實驗值,偏差分布非常集中,所有分子的偏差范圍都集中在±32 kJ·mol-1的范圍內,而且偏差在±4 kJ·mol-1范圍內的分子個數有63個,明顯好于O3LYP的計算結果.MLR盡管也能在一定程度上對O3LYP的計算結果進行校正,但其模型預測能力較差.

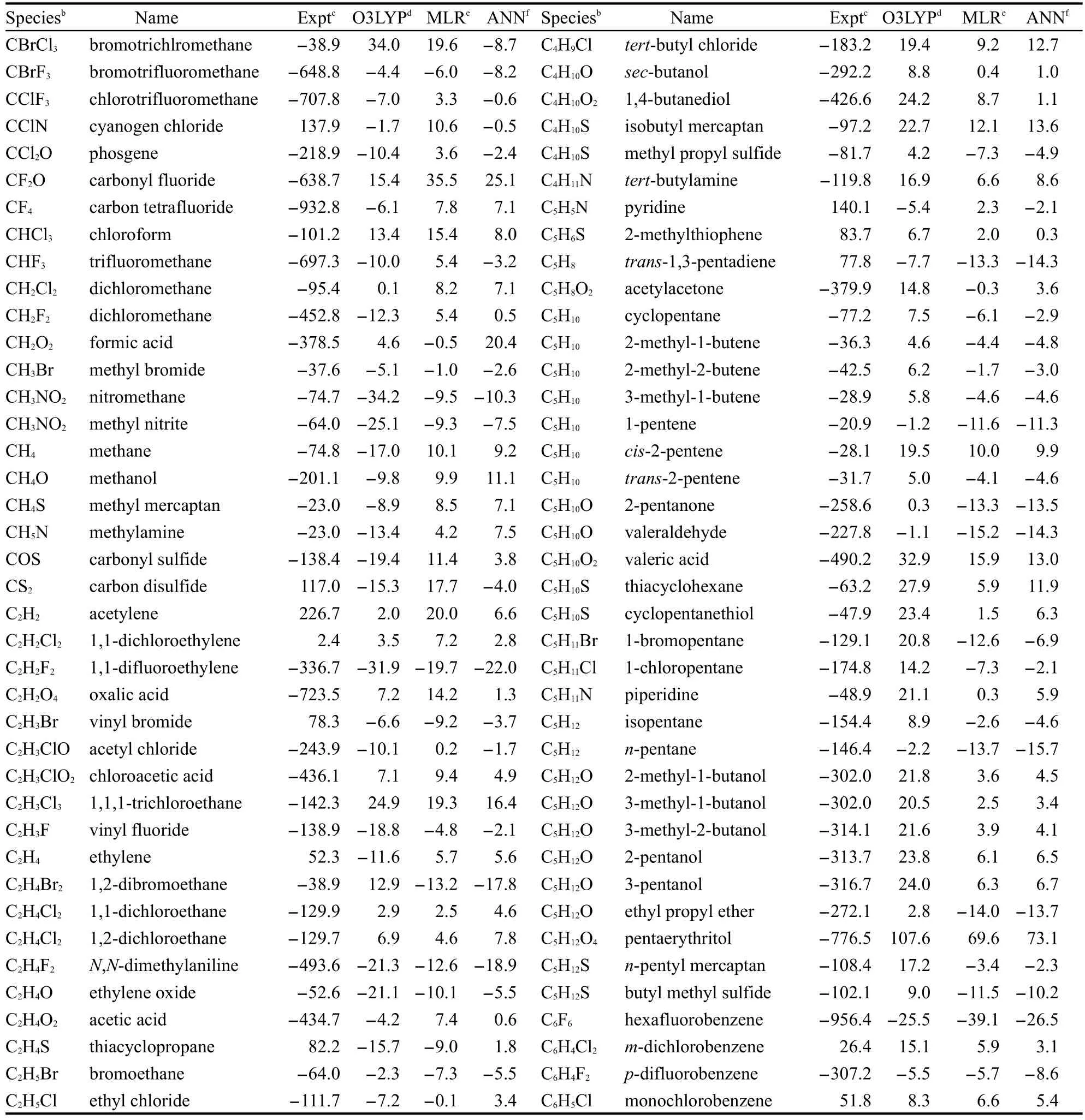
表3 ΔfH?的實驗值和不同方法的計算值和實驗值間的偏差aTable 3 Experimental ΔfH?and the deviation between the calculated and experimental values with different methodsa

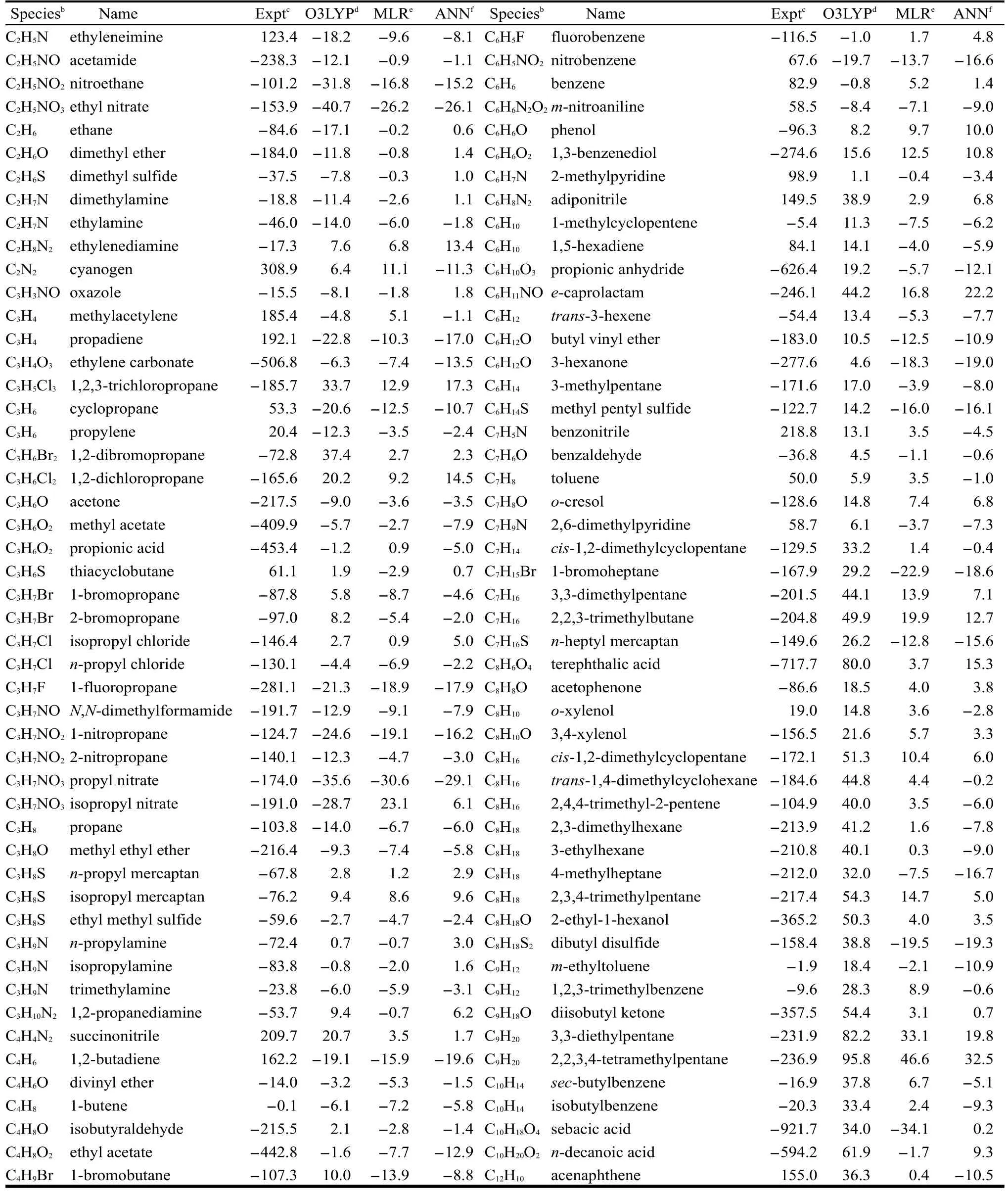
continued Table 3

表4 測試集ΔfH?的實驗值和不同方法的計算值和實驗值間的偏差aTable 4 Experimental ΔfH?of testing set and the deviation between the calculated and experimental values with different methodsa

180個訓練集分子經ANN校正后的結果列于表3.為了對比,表3中也列出了O3LYP的計算值與實驗值間的偏差,MLR得到的方程(1)擬合的計算值與實驗值間的偏差及全部分子的ΔfH?實驗值.

綜上所述,不管是模型的擬合還是模型的預測,利用ANN校正生成熱的結果要明顯優于MLR模型.原因可能是ANN模型采用了Sigmod函數來校正理論生成熱,而MLR模型不是利用非線性函數.在ANN模型里,每個輸入的參數都與隱藏層的神經元有一定的關系,而本文所采用的ANN模型的輸入層中包含一個偏置量,而且隱藏層包含三個神經元,因此ANN在擬合的過程中產生的變量數目要比MLR多,而在MLR方法中,變量的數目與輸入的參數數目相同.

3.3 獨立測試集的預測結果

為了驗證MLR和ANN模型的預測能力,我們取出40個分子建立了一個獨立測試集,經過MLR和ANN模型校正后,測試集分子生成熱的RMSD從21.3 kJ·mol-1分別降低到12.1、10.4 kJ·mol-1.因此,ANN模型的預測能力要優于MLR模型.表4列出了獨立測試集分子經MLR和ANN校正后的結果,同時也列出了生成熱的O3LYP計算值與實驗值間的偏差.

4 結論

采用O3LYP/6-311+G(3df,2p)//O3LYP/6-31G(d)計算220個有機分子的生成熱,然后采用ΔfH?calc、雙中心成鍵電子數、雙中心反鍵電子數、單中心價層孤對電子數、單中心的內層電子數、原子總數和氫原子個數、分子的零點能作為描述符參數,運用神經網絡方法和多元線性回歸方法對生成熱進行校正.研究結果表明:經過神經網絡校正后,ΔfH?的理論計算值與實驗值間的RMSD從24.7 kJ·mol-1降低到11.8 kJ·mol-1,ANN模型的標準回歸系數是0.96, MLR雖然在一定程度上降低了生成熱的RMSD,但是它的標準回歸系數很小,說明MLR的預測能力很差.采用ANN和MLR模型校正40個獨立測試集分子的生成熱,結果表明其RMSD從21.3 kJ·mol-1分別降低到10.4、12.1 kJ·mol-1.因此ANN模型的擬合和預測能力要明顯優于MLR.在利用統計方法校正能量時,描述符的選取是問題的關鍵,因此有必要選擇合適的描述符,從而進一步改善統計方法對理論計算獲得的能量的校正結果.

(1) Pedley,J.B.;Naylor,R.D.;Kirby,S.P.Thermochemical Data of Organic Compounds;Chapman and Hall:New York,1986.

(2)Yaws,C.L.Chemical Properties Handbook;McGraw-Hill: New York,1999.

(3) Lide,D.R.CRC Handbook of Chemistry and Physics,3rd. electronic ed.;BocaRaton:FL,2000.

(4) Wu,J.;Xu,X.J.Chem.Phys.2007,127,214105.doi:10.1063/ 1.2800018

(5) Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Pople,J.A. Chem.Phys.Lett.1997,270,419.doi:10.1016/S0009-2614(97) 00399-0

(6) Schmitz,L.R.;Chen,K.H.;Labanowski,J.;Allinger,N.L. J.Phys.Org.Chem.2001,14,90.doi:10.1002/1099-1395 (200102)14:2＜90::AID-POC330＞3.0.CO;2-O

(7) Curtiss,L.A.;Raghavachari,K.;Trucks,G.W.;Pople,J.A. J.Chem.Phys.1991,94,7221.doi:10.1063/1.460205

(8) Lado-Tourino,I.;Tsobnang,F.Comp.Mater.Sci.1998,11,181. doi:10.1016/S0927-0256(98)80004-9

(9) Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Pople,J.A. J.Chem.Phys.2000,112,7374.doi:10.1063/1.481336

(10) Wodrich,M.D.;Corminboeuf,C.;Schleyer,P.v.R.Org.Lett. 2006,8,3631.doi:10.1021/ol061016i

(11) Check,C.E.;Gilbert,T.M.J.Org.Chem.2005,70,9828.doi: 10.1021/jo051545k

(12) Izgorodina,E.I.;Coote,M.L.;Radom,L.J.Phys.Chem.A 2005,109,7558.doi:10.1021/jp052021r

(13) Schreiner,P.R.;Fokin,A.A.;Pascal,R.A.,Jr.;de Meijere,A. Org.Lett.2006,8,3635.doi:10.1021/ol0610486

(14)Zhao,Y.;Gonzalez-Garcia,N.;Truhlar,D.G.J.Phys.Chem.A 2005,109,2012.doi:10.1021/jp045141s

(15) Zhang,I.Y.;Luo,Y.;Xu,X.J.Chem.Phys.2010,132,194105. doi:10.1063/1.3424845

(16) Cohen,A.J.;Handy,N.C.Mol.Phys.2001,99,607.doi: 10.1080/00268970010023435

(17)Yang,K.;Peverati,R.;Truhlar,D.G.;Valero,R.J.Chem.Phys. 2011,135,044118.doi:10.1063/1.3607312

(18) Heerdt,G.;Morgon,N.H.Quimica Nova 2011,34,868.doi: 10.1590/S0100-40422011000500024

(19) Bochevarov,A.D.;Friesner,R.A.;Lippard,S.J.J.Chem. Theory Comput.2010,6,3735.doi:10.1021/ct100398m

(20)Dobado,J.A.;Gomez-Tamayo,J.C.;Calvo-Flores,F.G.; Martinez-Garcia,H.;Cardona,W.;Weiss-Lopez,B.;Ramirez-Rodriguez,O.;Pessoa-Mahana,H.;Araya-Maturana,R.Magn. Reson.Chem.2011,49,358.doi:10.1002/mrc.2745

(21) Qian,Z.S.;Feng,H.;He,L.N.;Yang,W.J.;Bi,S.P.J.Phys. Chem.A 2009,113,5138.doi:10.1021/jp810632f

(22) Strassner,T.;Taige,M.A.J.Chem.Theory Comput.2005,1, 848.doi:10.1021/ct049846+

(23) Baker,J.;Pulay,P.J.Comput.Chem.2003,24,1184.doi: 10.1002/jcc.10280

(24) Curtiss,L.A.;Jones,C.;Trucks,G.W.;Raghavachari,K.; Pople,J.A.J.Chem.Phys.1990,93,2537.doi:10.1063/ 1.458892

(25) Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Pople,J.A. J.Chem.Phys.1997,106,1063.doi:10.1063/1.473182

(26) Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Rassolov,V.; Pople,J.A.J.Chem.Phys.1998,109,7764.doi:10.1063/ 1.477422

(27) Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Pople,J.A. J.Chem.Phys.2000,112,7374.doi:10.1063/1.481336

(28) Curtiss,L.A.;Redfern,P.C.;Raghavachari,K.Chem.Phys. Lett.2010,499,168.doi:10.1016/j.cplett.2010.09.012

(29) Dorofeeva,O.V.;Kolesnikova,I.N.;Marochkin,I.I.;Ryzhova, O.N.J.Struct.Chem.2011,22,1303.doi:10.1007/s11224-011-9827-7

(30)Hu,L.H.;Wang,X.J.;Wong,L.H.;Chen,G.H.J.Chem. Phys.2003,119,11501.doi:10.1063/1.1630951

(31)Wang,X.J.;Wong,L.H.;Hu,L.H.;Chan,C.Y.;Su,Z.M.; Chen,G.H.J.Phys.Chem.A 2004,108,8514.doi:10.1021/ jp047263q

(32)Duan,X.M.;Li,Z.H.;Song,G.L.;Wang,W.N.;Chen,G.H.; Fan,K.N.Chem.Phys.Lett.2005,410,125.doi:10.1016/ j.cplett.2005.05.046

(33)Duan,X.M.;Song,G.L.;Li,Z.H.;Wang,X.J.;Chen,G.H.; Fan,K.N.J.Chem.Phys.2004,121,7086.doi:10.1063/ 1.1786582

(34) Yan,G.K.;Li,J.J.;Li,B.R.;Hu,J.;Guo,W.P.J.Theor. Comput.Chem.2007,6,495.doi:10.1142/ S0219633607003118

(35) Zheng,X.;Hu,L.;Wang,X.;Chen,G.Chem.Phys.Lett.2004, 390,186.doi:10.1016/j.cplett.2004.04.020

(36) Zhang,J.H.;Wang,X.J.Acta Phys.-Chim.Sin.2010,26, 188. [張家虎,王秀軍.物理化學學報,2010,26,188.] doi:10.3866/PKU.WHXB20100116

(37) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 09, Revision B.01;Gaussian Inc.:Wallingford,CT,2010.

(38) Zheng,W.F.;Tropsha,A.J.Chem.Inf.Comput.Sci.2000,40, 185.doi:10.1021/ci980033m

(39) Cramer,R.D.,III;Patterson,D.E.;Bunce,J.D.J.Am.Chem. Soc.1988,110,5959.doi:10.1021/ja00226a005

(40) Golbraikh,A.;Tropsha,A.J.Chem.Inf.Comput.Sci.2003,43, 144.doi:10.1021/ci025516b

April 9,2012;Revised:July 16,2012;Published on Web:July 17,2012.

Statistical Correction of Heat of Formation Calculated by the O3LYP Method

WANG Xiu-Jun*LONG Mi
(Key Laboratory of Fuel Cell Techology of Guangdong,College of Chemistry and Chemical Engineering, South China University of Technology,Guangzhou 510640,P.R.China)

The results of density functional theory calculations are known to contain inherent numerical errors caused by various intrinsic approximations.In this paper,O3LYP/6-311+G(3df,2p)//O3LYP/6-31G(d) calculations were used to derive the heats of formation(ΔfH?calc)of 220 small to medium-sized organic molecules,followed by the application of artificial neural network(ANN)and multiple linear regression (MLR)analyses to correct the values.The physical descriptors chosen were ΔfH?calcand zero point energy as well as the total quantities of atoms,hydrogen atoms,2-center bonds,2-center antibonds,1-center valence lone pairs and 1-center core pairs.The ANN and MLR systems were initially constructed using a 180 training set.The trained ANN and MLR systems were subsequently used to predict values of ΔfH?calcfor a 40 individual testing set.The results demonstrated that the root mean square(RMS)deviations between the calculated and experimental ΔfH?values in the training set were reduced from 24.7 to 11.8 and 13.0 kJ· mol-1after ANN and MLR corrections,respectively.For the individual testing set,the deviations(RMSD) were reduced from 21.3 to 10.4 and 12.1 kJ·mol-1,respectively.Based on these results,it can be concluded thatANN exhibits superior fitting and predictive abilities compared with MLR.

O3LYP;Neural network;Multiple linear regression;Heat of formation;Root mean square deviation

10.3866/PKU.WHXB201207172

?Corresponding author.Email:xjwangcn@scut.edu.cn;Tel:+86-20-87112943.

The project was supported by the National Natural Science Foundation of China(20975040)and Natural Science Foundation of Guangdong Province,China(10351064101000000).

國家自然科學基金(20975040)及廣東省自然科學基金(10351064101000000)資助項目

O641