雙層黏彈介質模型條件下地震應力擾動的時空特征

蔣海昆，吳 瓊，宋 金，李 金，曲均浩

1 中國地震臺網中心，北京 100045

2 中國地震局地震預測研究所，北京 100036

3 中國地震局地質研究所，北京 100029

雙層黏彈介質模型條件下地震應力擾動的時空特征

蔣海昆1，吳 瓊1，宋 金1，李 金2，曲均浩3

1 中國地震臺網中心，北京 100045

2 中國地震局地震預測研究所，北京 100036

3 中國地震局地質研究所，北京 100029

基于簡化雙層黏彈介質模型及其變形過程的時間屬性，考慮震后地殼上層（黏滯性相對較弱）短時間的彈性擾動及后續較長時間內下層（黏滯性相對較強）黏性變形對上層應力擾動的聯合作用，研究地震應力擾動的時空變化.結果顯示，地震應力擾動在震后一段時間內逐漸增大，之后緩慢衰減.并且模型參數越接近真實地體，應力擾動增大及衰減過程就越緩慢，持續時間越長，即地震活動具有較長時期的時間“記憶”特性.因而，在地震活動及庫侖應力變化研究中，長時期的應力擾動影響不宜忽略.地震應力擾動有一定的空間作用范圍，在此范圍內應力擾動隨距離衰減明顯，距離震源較近處衰減較快、距離震源較遠處衰減相對較慢，此范圍之外應力擾動可忽略不計.在本文所取與實際地殼相對較為接近的模型參數條件下，應力擾動的空間作用范圍大體是震源線性破裂尺度的2.5倍.地震應力擾動隨震級增大而逐漸增大，在本文模型參數條件下，震級大于6級之后，應力擾動隨震級快速增加.地震破裂尺度測量誤差所導致的應力擾動計算誤差的相對大小，與時間無關，與破裂尺度（震級）及震源距有關，隨震源距的增大而增大，但對應力擾動的總體變化趨勢及變化范圍影響甚微.當距離足夠遠時，應力擾動計算誤差的相對大小趨于常數，就6、7、8級地震而言，最大應力擾動計算誤差分別小于應力擾動值本身的22%、30%及38%.

雙層黏彈介質地殼模型，地震應力擾動，持續時間，作用范圍，主震震級

1 引 言

一次地震發生后，地震斷層永久位移產生的小的“靜態”應力變化，可以改變附近斷層上發生地震的可能性，或者說可能觸發地震［1］.許多近場的觸發地震、特別是觸發余震的研究，將這種靜態應力變化視為觸發因素，并認為其與斷層上的負載變化等價［2－3］.已有研究表明，大多數余震發生在庫侖破裂應力增加的區域［1］，地震活動率在庫侖破裂應力增加的區域增大、在庫侖破裂應力減小的區域降低［4］，即大地震導致的區域應力變化是區域地震活動增強的原因.例如，1992年Landers7.3級地震后，余震分布在庫侖破裂應力增加大于0.03MPa的區域［4］，震后在距離Landers地震主斷層5～75km的范圍內，85%的余震事件與靜應力增加相一致［5］.事實上，關于斷裂之間相互作用、以及與地震活動之間的關系，早在1960～1980年代即已進行過深入的探討［6－14］，當時已知一次較強地震的位錯在周圍區域產生的靜態庫侖應力變化一般是10－2～10－1MPa量級，但認為這很難導致或觸發另一次地震的發生，因為根據巖石摩擦實驗結果，地殼中、上部最大摩擦強度可能是幾千兆帕［15］.但1980年代以來，隨著非線性動力學的發展，認為地球動力系統處于自組織臨界狀態［16］，而臨界狀態下微小的應力擾動即可觸發地震活動.

存在的問題是，具有有效觸發影響的庫侖應力變化量值及影響范圍究竟如何？關于前者，全球研究結果的綜述表明［17］，庫侖破裂應力變化大于10－1～10－2MPa即有可能觸發余震或后繼地震，這一應力變化量值，比月相潮汐應力（約10－3MPa）大約101～102倍.關于后者，檢測應力擾動有效范圍的最理想方法，是在足夠大的區域開展應力的直接測量，但這實際上無法實現.理論上，一般認為應力場空間結構的時間演化，是由相對穩定的遠場背景應力與局部應力擾動的疊加，同時耦合有非常復雜的地殼流變響應.為合理估計應力擾動及其隨時間的演變，需要局部巖石圈的精確流變學模型，包括黏滯層彈性常數及松弛時間等數據，這些數據在大尺度上可由地球物理學調查、推論得到，但由于結構的復雜性，確定精確的模型參數仍存在諸多困難［18］.幸運的是，依據臨界點理論，只要背景應力變化在時間尺度上足夠緩慢，應力擾動即可視為僅與地震發生有關，而不屬于大尺度邊界力學條件產生的影響.因而，針對不長的研究時間段內（數月至數十年）的地震活動過程，可以暫不考慮應力場遠場邊界條件的影響.根據這一特點，為研究有限時空尺度內應力場的波動問題，Ouillon等提出一種簡化的地殼流變學模型［19］，它突出了黏彈性分層介質內部應力傳播和松弛這一本質特征，而對其他可能的影響因素則進行了簡化.事實上，我國20世紀八、九十年代在大陸構造應力場和應變傳播的數值模擬研究中，也已開始引入彈塑性或黏彈性理論［20－21］，從地幔及下地殼塑性流動特性出發，對殼幔力學行為、大尺度塑性流動網絡構造及其應力、應變特性等開展了許多理論、物理模擬及數值模擬實驗研究［22－24］，近期部分關于庫侖應力觸發的研究也開始引入黏彈性質［25－28］.

本文將基于文獻［19］模型，考慮雙層黏彈介質及其變形過程的時間屬性，假定地震對某處的應力擾動包含短時間的彈性擾動及較長時間的黏性變形擾動兩部分，在簡化模型的前提下，討論地震應力擾動的時、空變化及與主震破裂尺度的關系等問題.

2 雙層黏彈介質模型中地震導致的應力擾動

Ouillon等［19］給出雙層黏彈介質模型中標量格林函數形式的應力擾動表達式.

假定震源輻射各向同性，且圍繞震源呈半徑對稱分布，則均勻彈性介質中點源產生的應力擾動（stress perturbation）隨震源距r衰減［19］：

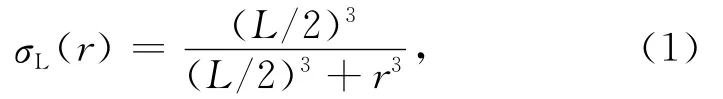
L為震源線性尺度.由于柱對稱的應力擾動σL（r）始終為正，因而σL（r）不是真實的應力，但可理解為一種影響函數，表征一次地震事件對應力場的可能影響，影響范圍由L控制.

進一步考慮最簡單的雙層黏彈介質模型，下層為半無限空間，上、下層黏彈介質松弛時間分別為τ1、τ2，τ1＞τ2.松弛時間的物理含義是，由于模型中黏性元件的黏滯作用，延緩了彈性元件的應力松弛或應變恢復，在應力松弛或應變恢復過程中，當應力或應變降低到初始值的1／e時所經歷的時間稱為松弛時間.因而從力學作用方式及應變松弛過程來看，該模型上、下層可簡單理解成剪切模量和剪切黏度不同的Maxwell體，上層還串聯有滑塊以模擬突然滑動的地震過程，模型上、下兩臂之間并行聯結（圖1）.

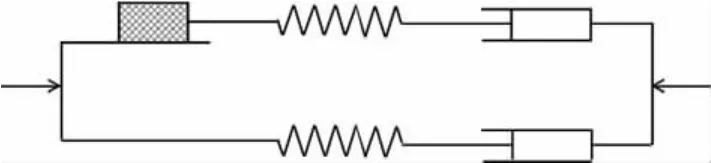
圖1 簡化的雙層黏彈介質模型示意圖Fig.1 Sketch map of the simplified two－layer viscoelastic medium model

假定地震發生在相對脆性的上層，地震導致的應力場瞬間的彈性解由式（1）給出.地震瞬間的彈性變形在上層產生一個直接的彈性應力加載，由于上層的黏彈性質，之后將在上層導致彈性應力松弛.與此同時，地震時介質瞬間彈性變形所導致的應力傳遞，亦將激發對下層的應力加載，同樣導致下層介質的黏滯松弛過程.由于下層黏滯性強于上層，其介質流動較上層更為容易，因而下層的黏滯松弛過程反過來對上層產生延遲加載，下層黏滯松弛過程對上層的加載影響表達為［19］

此處σL（r）是由式（1）給出的彈性各向同性解，C是表征上層應力遷移最大量值的常數，與模型幾何結構有關，若C＝0則沒有應力轉移.H（t）為Heaviside函數，其作用是確保一旦地震發生，其應力波動不為零.t是自地震之后的流逝時間.這一時期，上層應力也按exp（－t／τ1）方式松弛.當上、下兩層黏彈介質松弛過程同時發生時，則上層總的應力擾動來源于兩部分的貢獻：其一是地震在上層產生瞬間彈性應力加載之后所導致的應力松弛σL（r）exp（－t／τ1），其二是地震后下層黏滯松弛在上層所導致的應力加載f（r，t）時間導數的卷積，f（r，t）具有指數形式exp（－t／τ1）的松弛特征.第二部分貢獻匯聚了由于下層松弛而在上層每單位時間所導致的應力源增加df（r，t）／dt.經過一定的數學處理之后，由于地震所導致的、總的應力擾動為［19］

r和t分別是震源距和地震之后的流逝時間.參數B是表征下層松弛對上層應力延遲加載作用強弱的常數，B強烈依賴于雙層黏彈介質模型各層的幾何及流變性質，其真實數值難以確定.B＝1意味著上、下兩層介質震后松弛過程所導致的應力擾動貢獻，與震級具有相同的量級；B＝0則表明僅考慮上層松弛過程而忽略下層的影響.如果研究點附近區域起算震級以上地震之間的平均時間間隔大于下層松弛時間τ2，則這種忽略對最終結果的影響非常小［19］.由于本文力圖研究雙層黏彈介質模型條件下的地震應力擾動，因而取B＝1.

式（1）及式（3）中的震源線性尺度L與地震破裂尺度或余震分布尺度相當.本文使用依據中國大陸143次主余型序列得到的統計關系［29］，經由震級M計算得到：

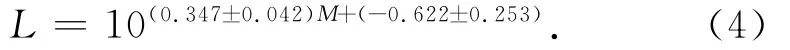
3 結果及討論

在實際地殼介質狀況下，上地殼松弛時間τ1介于數千至數十萬年之間，下地殼松弛時間τ2介于數年至數百年之間，主要與剪切模量G及剪切黏度η有關（表1）［22］.為從概念上探討簡化雙層黏彈介質模型條件下，上、下層介質黏滯性質對地震應力擾動的影響，以下選擇三種τ1、τ2組合進行討論（單位為“月”），分別是：（1）τ1＝1200、τ2＝120；（2）τ1＝120、τ2＝12；（3）τ1＝12、τ2＝4.三種情形地殼上、下層的流變性均大大高于實際，其中第一種情況在量級上與實際相對接近.

已有研究表明，地震庫侖破裂應力變化大于10－1～10－2MPa即有可能觸發地震［17］.一般而言，小震應力降可粗略地視為常數［30］，但對破裂尺度明顯大于震源深度的大地震，在記錄頻段確定的情況下，應力降與震級、震源深度定性正相關［31－33］，與破裂類型也有一定關系［34］.總體而言，不同區域、不同時段、不同震級范圍地震應力降分布于10－2～102MPa，絕大多數介于100～101MPa之間（中位值）.例如，利用地下2.5km深井地震儀記錄的圣安德列斯斷層附近100多次ML1.0～5.0級地震資料計算的應力降中位值約為3MPa［35］，舊金山灣1998—2007年間529次M1.0～4.2級地震的應力降中位值約為8.7MPa［33］；1900—1998年全球7400余次MS4.0～8.2級地震應力降中位值約為2.3MPa［36］，等等.由于震時（t＝0）震源地方（r＝0）的應力擾動與地震應力降相當，因而10－1～10－2MPa這一能夠觸發地震活動的庫侖應力變化量值，粗略地相當于大多數地震應力降的10－1～10－2倍.另一方面，τ1＝1200、τ2＝120條件下，由無量綱標量函數式（3）得到的震時震源地方的應力擾動等于1（參見圖2a線（1）及圖3a中最下邊一條曲線所示），對比上述庫侖應力變化觸發地震的研究結果，為方便問題討論，本文簡單地取0.01為應力擾動的“有效”值，0.01大體相當于τ1＝1200、τ2＝120條件下震時震源地方應力擾動的10－2倍.

表1 地殼介質的松弛時間［22］Table 1 The relaxation time of crust medium［22］

3.1 地震應力擾動隨時間的變化

圖2 不同距離地震應力擾動隨時間的變化（a）r＝0；（b）r＝50km；（c）r＝100km.（1）τ1＝1200、τ2＝120；（2）τ1＝120、τ2＝12；（3）τ1＝12、τ2＝4；τ1、τ2單位為“月”；M＝7.0.Fig.2 Variation of earthquake stress perturbation with the distance

為簡化討論，統一取式（4）中主震震級M＝7.0.圖2給出不同區域地震應力擾動隨時間的變化，可見對與實際較為接近的τ1、τ2組合（τ1＝1200、τ2＝120），震源地方（r＝0）應力擾動在震后隨時間緩慢增加，這一過程大體上可持續20年（約220個月），之后緩慢減小，減小過程亦可持續數十年（圖2a線（1））；若增大雙層黏彈介質的黏滯性質，取τ1＝120及τ2＝12（圖2a線（2）），則震后不長的時間內（約22個月），震源地方應力擾動增強明顯，之后隨時間持續減小，減小速率亦逐漸變小，50多年后（約643個月）應力擾動小于0.01；進一步增大雙層黏彈介質的黏滯性質，取τ1＝12及τ2＝4（圖2a線（3），這是一種遠離實際的情形），這種條件下，震后極短的時間內（約4個月），震源地方應力擾動快速增長，之后隨時間快速降低，大約5.5年（約66個月）后應力擾動已趨于0（＜0.01）.

r＝50km及r＝100km處應力擾動隨時間的變化分別如圖2b及圖2c所示，圖中曲線（1）、（2）、（3）含義與圖2a相同，可見不同τ1、τ2組合條件下應力擾動隨時間的變化趨勢與圖2a類似，應力擾動最強的時間T1也與圖2a震源地方的相同，但應力擾動強度有顯著差異（圖2，表2）.對相同的震源距r，雙層黏彈介質模型黏滯性越強，應力擾動衰減到小于0.01所需的時間T2越短.例如就震源地方（r＝0）而言，對與實際較為接近的τ1、τ2組合（τ1＝1200、τ2＝120），應力擾動隨時間衰減緩慢，T2遠大于本文的最大模擬時間（60年）；增大雙層黏彈介質模型的黏滯性質，當τ1＝120、τ2＝12時，T2≈54年；繼續增大模型的黏滯性，取τ1＝12、τ2＝4，則T2≈5.6年.對相同的雙層黏彈介質模型（相同τ1、τ2組合），應力擾動衰減到小于0.01的時間T2隨震源距r的增大而減小，例如對τ1＝120、τ2＝12的模型參數組合，r＝0、50及100km所對應的T2分別約為54、38及19年（表2第5列）.

表2 不同模型參數及震源距條件下應力擾動最強的時間（T1）及應力擾動趨于0的時間（T2）Table 2 The time of maximum stress perturbation and the time of stress perturbation tends to 0，with different model parameters and in different distance

3.2 地震應力擾動隨空間距離的衰減

取雙層黏彈介質模型上、下兩層松弛時間τ1＝1200月、τ2＝120月.假定地震在上層發生，分別選取t＝0、t＝6月、t＝12月及t＝24月等四個震后時間點，研究震后不同時刻地震應力擾動隨震源距r的變化，結果如圖3所示，圖3a、3b分別為震級M＝7.0和M＝6.0時的結果.在所選定的黏彈介質模型條件下（τ1＝1200、τ2＝120），當主震震級M＝7.0時（圖3a），50km范圍內應力擾動隨距離衰減較快，之后逐漸變緩，大約150km范圍之外，應力擾動趨于0（＜0.01）；降低主震震級至M＝6.0（圖3b），30km范圍內應力擾動隨距離衰減較快，之后逐漸變緩，大約60～70km范圍之外，應力擾動趨于0（＜0.01）.簡言之，①震后同一時刻應力擾動隨震源距r的增加而快速減小；②較大地震應力擾動的有效作用距離相對較大；③同一地方應力擾動隨時間增加而略有增大，震源距r越小的地方增加越明顯.

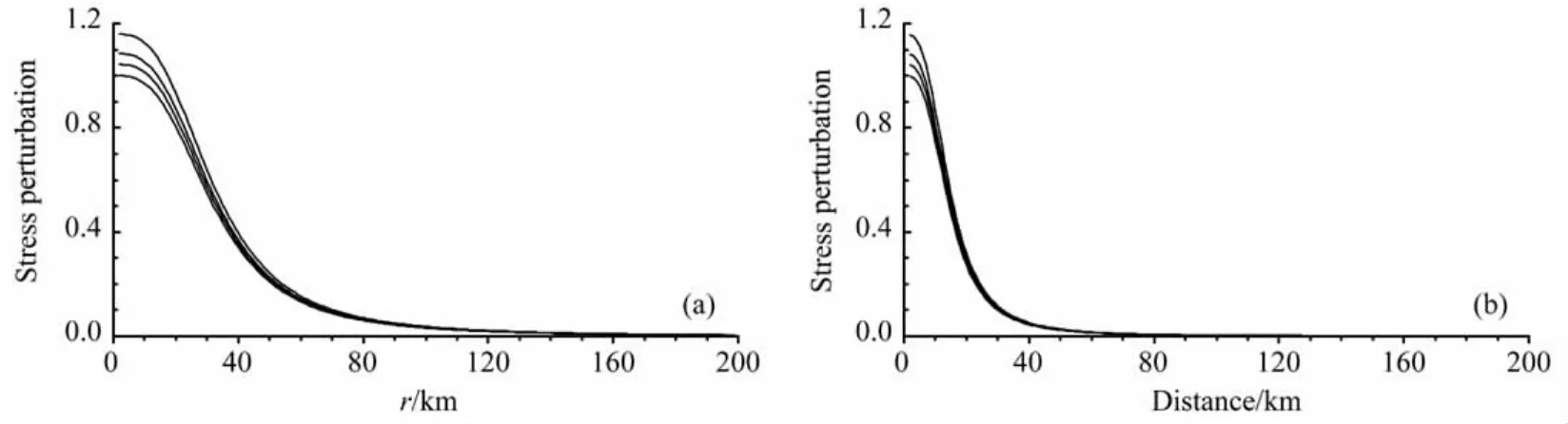
圖3 不同時刻地震應力擾動隨距離的變化（τ1＝1200、τ2＝120；τ1、τ2單位為“月”）（a）M0＝7.0，曲線從上到下依次對應t＝24、t＝12、t＝6及t＝0的結果（t單位為“月”）；（b）M0＝6.0，曲線從上到下依次對應t＝24、t＝12、t＝6及t＝0的結果（t單位為“月”）.Fig.3 Variation of stress perturbation with distance in different time（τ1＝1200，τ2＝120；The unit ofτ1andτ2is month）

3.3 地震強度對應力擾動的影響

參考上述關于應力擾動隨時間和距離變化的研究結果，取雙層黏彈介質模型上、下兩層松弛時間τ1＝1200、τ2＝120（單位為“月”），考察震后220個月時（t＝220）空間上不同距離處應力擾動隨震級的變化，220個月大體上相當于τ1＝1200、τ2＝120條件下應力擾動達到最大的時間（參見圖2及表2），結果如圖4所示.可見震源地方（r＝0，線（1））應力擾動不隨地震震級大小而變化，這從式（3）亦可看出，時間t確定之后，應力擾動決定于線性震源尺度L（L∝10M，M為地震震級）及震源距r，r＝0時應力擾動為常數，這與常應力降模型或不同震級地震應力降差異不大這一觀測事實定性一致［37－38］.對遠離震源地方的區域（r＞0），應力擾動（線（2）、（3）、（4））總體上隨震級增大而增大，與破裂尺度隨震級的變化趨勢（空心圓）大體類似.對相同大小的地震，距離越近（r越小）應力擾動越大、距離越遠（r越大）應力擾動越小；對距離固定的區域，較低震級地震（例如M＜6）應力擾動非常弱，震級大于6級之后，應力擾動隨震級快速增加，但當震級非常大的時候（例如M＞8），應力擾動隨震級的增幅逐漸變緩.具體來看，對τ1＝1200、τ2＝120的模型參數，震后220個月的時候，震源距r分別為50、100及200km的地方，所導致應力擾動大于0.01的地震震級分別應大于5.5、6.4和7.2級.由式（4）可知，上述三個震級對應的線性震源尺度大約分別為19、43及88km，因而50、100及200km距離分別約為上述破裂尺度的2.5～2.6倍.為對比，取t＝20進行類似計算，所得上述比例大約介于2.2～2.4之間，而τ1＝1200、τ2＝120這一模型參數條件下，地震應力擾動在t＝20時并未達到最大.換言之，在所取與實際較為接近的雙層黏彈模型參數條件下，最大的有效應力擾動范圍約為震源線性破裂尺度的2.5倍，對更遠地方的應力擾動可忽略不計.

圖4 不同距離處應力擾動（左，震后220個月的結果）、破裂尺度（右，空心圓）隨震級的變化τ1＝1200、τ2＝120，t＝220.（1）r＝0；（2）r＝50km；（3）r＝100km；（4）r＝200km.Fig.4 Variation of stress perturbation（left，the results of 220months since the mainshock）and fracture size（right，empty circle）with the magnitude

3.4 地震破裂尺度測量誤差對應力擾動的影響

除少數大地震震后有較為深入的野外考察外，地震破裂尺度大多依據余震分布范圍或依據統計關系粗略得到.由于震級測量及余震定位等因素的不精確性，以往地震破裂尺度與主震震級的統計關系（4）式存在較大的離散（參見文獻［29］），由此導致破裂尺度測量存在誤差，近似條件下，這種誤差或離散體現在（4）式回歸參數的變化上.

為討論破裂尺度測量誤差對應力擾動計算的影響，將（4）式寫為

分別求L對a、b的偏導數：

兩式相加有：

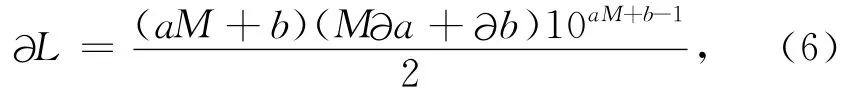
（6）式中?L可理解為由于回歸系數a、b的誤差?a、?b所導致的L的誤差.

利用式（3）求σ（r，t）對L的偏導數：

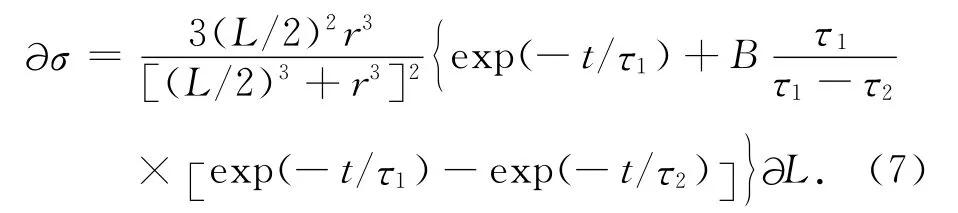
?σ是由于L的測量誤差?L所導致的σ的計算誤差.考慮?σ對σ的相對變化，并將（5）、（6）式代入（7）式有

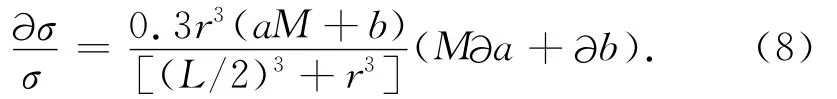
（8）式給出由于破裂尺度測量誤差（以?a、?b表達）所導致應力擾動計算誤差的相對大小（?σ／σ），可見（?σ／σ）與時間無關，與破裂尺度L（主震震級）及震源距r有關.若震源距r足夠大，則（?σ／σ）→0.3（aM＋b）（M?a＋?b），此即應力擾動計算誤差的極限.

將（4）式中有關參數a＝0.347、?a＝0.042，b＝－0.622、?b＝0.253代入（8）式，并設定其中M＝7.0，數值計算結果顯示，應力擾動計算誤差的相對大小（?σ／σ）隨震源距r的增大而增加，r小于30km時，應力擾動的計算誤差小于應力擾動值的10%，r小于40km時小于20%，r小于200km時小于30%.關于應力擾動計算誤差相對大小的極限值，對6、7、8級地震而言，r→∞＋時，（?σ／σ）分別趨于0.221、0.297及0.381.

取M＝7.0、t＝0、以及τ1＝1200、τ2＝120，圖5給出圖3a中最下面一條曲線的結果，其中誤差棒表示由于破裂尺度的測量誤差所導致的應力擾動計算誤差?σ，可見對應力擾動的總體變化趨勢并無影響.并且，盡管應力擾動計算誤差的相對大小（?σ／σ）隨震源距r的增大而增加，但由于應力擾動本身隨震源距快速衰減，因而絕對誤差?σ并不隨距離增大而無限制地增大.

圖5 t＝0時刻地震應力擾動隨距離的變化（τ1＝1200、τ2＝120；τ1、τ2單位為“月”）誤差棒表示由于破裂尺度的測量誤差所導致的應力擾動計算誤差.Fig.5 Variation of stress perturbation with the distance at the time of t＝0（τ1＝1200，τ2＝120；The unit ofτ1andτ2is month）

4 結 論

引入簡化的雙層黏彈介質模型及其變形過程的時間屬性，考慮震后應力擾動為短時彈性應力擾動及后續較長時間下層黏性變形對脆性層（上層）應力擾動的累積，研究地震應力擾動的時空變化.主要結論如下：

（1）地震應力擾動在震后不長的時間內逐漸增大，之后緩慢衰減，并且雙層黏彈介質模型上、下層松弛時間越接近真實地體，地震應力擾動逐漸增大及之后的緩慢衰減過程就越緩慢，作用持續時間越長.這意味著，地震活動具有較長時期的時間“記憶”特性.這與Ouillon等提出的多分形應力激活模型（multifractal stress activation model）［39］相吻合，這一模型有兩點重要預期，一是引發地震破裂的激活過程與當地應力的指數增長有關，二是應力擾動具有長效記憶性.

（2）地震應力擾動隨地震震級增大而逐漸增大，在本文假定的與實際相對接近的模型參數條件下，震級大于6級之后，應力擾動隨震級快速增加.

（3）地震應力擾動隨距離衰減明顯，距離較近處衰減較快、距離較遠處衰減相對較慢.地震應力擾動有一定的空間作用范圍，粗略來看，在本文所取與實際地殼較為接近的模型參數條件下，應力擾動的空間作用范圍大體上是震源線性破裂尺度的2.5倍，超過此范圍的區域，應力擾動已經非常小（趨于0），可忽略不計.

需要指出的是，這一認識是基于點源模型、假定所有能量均在破裂起始點處釋放得到的結果，其應力擾動有效的空間影響范圍限于破裂尺度的數倍.對大地震而言，例如5·12汶川8.0級地震，其地表破裂尺度已近240km［40］，震源時間函數接近60s［41］，這時再把整個地震過程看作點源顯然不當.一種變通的考慮是，可把破裂過程離散化，整個破裂過程作為一系列移動點源的積分，點源的強度參考震源時間函數確定.可以預見，如此處理所得到的應力擾動影響范圍，在量級上與前述結果相比不會有明顯的變化.上述結果及認識可得到實際觀測結果的定性驗證［42］.在2008年5月12日汶川Ms8.0級大震前一周，采用水壓致裂技術在龍門山斷裂帶北段ZK1測點地下300～400m深度上測得的最大水平主應力值為21～22MPa，與其附近下盤ZK4測點最大水平主應力值之差高達8～10MPa；汶川地震后原地重復測量結果表明，發震斷裂帶上ZK1測點的最大、最小水平主應力值分別降低了29%和23%，而下盤ZK4測點的地應力狀況并無變化，ZK1與ZK4測點之間距離不過40多公里.盡管地震應力擾動的作用時間不足夠長，并且下盤ZK4測點不在破裂的傳播方向上，但作為一次8級巨大地震，其應力擾動隨距離的衰減可謂相當明顯.

（4）由于震級測量及余震定位等因素的不精確性，破裂尺度的測量或計算存在誤差，由此導致的應力擾動計算誤差的相對大小與時間無關，與破裂尺度L（主震震級）及震源距r有關，隨震源距r的增大而增加，但對應力擾動的總體變化趨勢及變化范圍影響非常小.當r趨于無窮時，應力擾動計算誤差的相對大小趨于常數.就6、7、8級地震而言，應力擾動計算誤差的最大值分別小于應力擾動值本身的22%、30%及38%.

（5）由于真實地體中地震產生的應力擾動衰減緩慢、持續時間長、顯示較長時期的時間“記憶”特性，因而地震活動及庫侖應力變化研究中，此前長時期的地震應力擾動影響不能忽略；由于地震產生的應力擾動隨距離衰減明顯，因而在開展靜態庫侖應力變化觸發地震活動研究時，應重點關注震中附近區域，較遠處則可能觸發作用不再明顯.由于震級不高時的應力擾動非常弱，因而通過庫侖應力變化研究未來地震區及其地震危險性時，以研究強震的庫侖應力變化為宜.

（References）

［1］ Harris R A.Introduction to special section：stress triggers，stress shadows，and implications for seismic hazard.J.Geophys.Res.，1998，103（B10）：24347－24358.

［2］ Toda S，Stein R S，Reasenberg P A，et al.Stress transferred by the 1995 Mw＝6.9Kobe，Japan，Shock：effect on aftershocks and future earthquake probabilities.J.Geophys.Res.，1998，103（B10）：24543－24565.

［3］ King G C P，Stein R S，Lin J.Static stress changes and the triggering of earthquakes.Bull.Seism.Soc.Am.，1994，84（3）：935－953.

［4］ Reasenberg P A，Simpson R W.Response of regional seismicity to the static stress change produced by the Loma Prieta earthquake.Science，1992，255（5052）：1687－1690.

［5］ Hardebeck J L，Nazareth J J，Hauksson E.The Static stress change triggering model：constraints from two southern California aftershock sequences.J.Geophys.Res.，1998，103（B10）：24427－24438.

［6］ Chinnery M A.The stress changes that accompany strike－slip faulting.Bull.Seism.Soc.Am.，1963，53（5）：921－932.

［7］ Smith S W，Van de Lindt W.Strain adjustments associated with earthquakes in southern California.Bull.Seism.Soc.Am.，1969，59（4）：1569－1589.

［8］ Rybichi K.Analysis of aftershocks on the basis of dislocation theory.Phys.Earth Planet Inter.，1973，7（4）：409－422.

［9］ 陳運泰，林邦慧，林中洋等.根據地面形變的觀測研究1966年邢臺地震的震源過程.地球物理學報，1975，18（3）：164－182.Chen Y T，Lin B H，Lin Z Y，et al.The focal mechanism of the 1966Hsingtai earthquake as inferred from the ground deformation observations.Chinese J.Geophys.（in Chinese），1975，18（3）：164－182.

［10］ Yamashina K.Induced earthquakes in the Izu Peninsula by the Izu－Hanto－Oki earthquake of 1974，Japan.Tectonophysics，1978，51（3－4）：139－154.

［11］ 黃福明，王廷韞.傾斜斷層錯動產生的應力場.地震學報，1980，2（1）：1－20.Huang F M，Wang T Y.The stress field of a dislocating inclined fault.Acta Seismologica Sinica（in Chinese），1980，2（1）：1－20.

［12］ 王仁，何國琦，殷有泉等.華北地區地震遷移規律的數學模擬.地震學報，1980，2（1）：32－42.Wang R，He G Q，Yin Y Q，et al.A mathematical simulation for the pattern of seismic transference in north China.Acta Seismologica Sinica（in Chinese），1980，2（1）：32－42.

［13］ 郭增建，秦保燕.大震重復性與減震作用.／／國家地震局科技司.近期強震危險性研究.北京：地震出版社，1989：455－456.Guo Z J，Qin B Y.Repeatability and weakening action of the large earthquakes.／／Department of Science ＆Technology，National Seismological Bureau.Study on the Recent Seismic Risk of Large Earthquakes（in Chinese）.Beijing：Seismological Press，1989：455－456.

［14］ Das S，Scholz C H.Off－fault aftershock clusters caused by shear stress increase？Bull.Seism.Soc.Am.，1981，71（1）：1669－1675.

［15］ Byerlee J D.Friction of rocks.PAGEOPH，1978，116（4－5）：615－626.

［16］ Bak P，Tang C.Earthquakes as a self－organized critical phenomena.J.Geophys.Res.，1989，94（B11）：15635－15638.

［17］ 萬永革，吳忠良，周公威等.幾次復雜地震中不同破裂事件之間的“應力觸發”問題.地震學報，2000，22（6）：568－576.Wan Y G，Wu Z L，Zhou G W，et al.“Stress triggering”between different rupture events in several earthquakes.Acta Seismologica Sinica（in Chinese），2000，22（6）：568－576.

［18］ Sornette D，Pisarenko V F.Fractal plate tectonics.Geophys.Res.Lett.，2003，30：1105，doi：10.1029／2002＿GL＿015043.

［19］ Ouillon G，Sornette D.Search for direct empirical spatial correlation signatures of the critical triggering earthquake model.Geophys.J.Int.，2004，157（3）：1233－1246.

［20］ 高祥林，羅煥炎，諾依格鮑爾H J.大陸碰撞動力學的三維數值模擬.地震地質，1987，9（2）：65－73.Gao X L，Luo H Y，Neugebauer H J.Three dimensional numerical modeling for the dynamics of the continental collision.Seismology and Geology（in Chinese），1987，9（2）：65－73.

［21］ 張東寧，許忠淮.青藏高原現代構造應力狀態及構造運動的三維彈粘性數值模擬.中國地震，1994，10（2）：136－143.Zhang D N，Xu Z H.Three dimensional elasto－visco numerical simulation of Qinghai－Xizang Plateau′s recent tectonic stress field and its motion.Earthquake Research in China（in Chinese），1994，10（2）：136－143.

［22］ 王繩祖，張四昌，田勤儉.大陸動力學：網狀塑性流動與多級構造變形.北京：地震出版社，2001：15－20.Wang S Z，Zhang S C，Tian Q J.Continental Dynamics：Netlike Plastic－Flow and Hierarchical Tectonic Deformation（in Chinese）.Beijing：Seismological Press，2001：15－20.

［23］ 臧紹先，寧杰遠，景志成.俯沖帶流變性質的研究.中國科學（D輯），2001，31（9）：705－711.Zang S X，Ning J Y，Jing Z C.Study on plastic－flow characteristics in subduction belt.Science in China（Series D）（in Chinese），2001，31（9）：705－711.

［24］ 于泳，洪漢凈，劉培洵等.粘彈性有限元與彈簧滑塊耦合模型——斷層與地塊相互作用的數值模擬.中國科學（D輯），2003，33（增刊）：82－90.Yu Y，Hong H J，Liu P X，et al.The viscoelastic finiteelement and the coupling model of the spring－sliding black——numerical simulation on the interaction between faults with the plate.Science in China（Series D）（in Chinese），2003，33（Suppl.）：82－90.

［25］ 沈正康，萬永革，甘衛軍等.東昆侖活動斷裂帶大地震之間的黏彈性應力觸發研究.地球物理學報，2003，46（6）：786－795.Shen Z K，Wan Y G，Gan W J，et al.Viscoelastic triggering among large earthquakes along the east Kunlun fault system.Chinese J.Geophys.（in Chinese），2003，46（6）：786－795.

［26］ 沈正康，萬永革，甘衛軍等.華北地區700年來地殼應力場演化與地震的關系研究.中國地震，2004，20（3）：211－228.Shen Z K，Wan Y G，Gan W J，et al.Crustal stress evolution of the last 700years in North China and earthquake occurrence.Earthquake Research in China（in Chinese），2004，20（3）：211－228.

［27］ 萬永革，沈正康，曾躍華等.唐山地震序列應力觸發的粘彈性力學模型研究.地震學報，2008，30（6）：581－593.Wan Y G，Shen Z K，Zeng Y H，et al.Study on visco－elastic stress triggering model of the 1976Tangshan earthquake sequence.Acta Seismologica Sinica（in Chinese），2008，30（6）：581－593.

［28］ 邵志剛，周龍泉，蔣長勝等.2008年汶川Ms8.0地震對周邊斷層地震活動的影響.地球物理學報，2010，53（8）：1784－1795.Shao Z G，Zhou L Q，Jiang C S，et al.The impact of Wenchuan Ms8.0earthquake on the seismic activity of surrounding faults.Chinese J.Geophys.（in Chinese），2010，53（8）：1784－1795.

［29］ 蔣海昆，鄭建常，吳瓊等.中國大陸中強以上地震余震分布尺度的統計特征.地震學報，2007，29（2）：151－164.Jiang H K，Zheng J C，Wu Q，et al.Statistical features of aftershock distribution size for moderate and large earthquakes in Chinese mainland.Acta Seismologica Sinica（in Chinese），2007，29（2）：151－164.

［30］ Aki K.Earthquake mechanism.Tectonophysics，1972，13（1－4）：423－446.

［31］ Hanks T C，Bakun W H.A bilinear source－scaling model for M－logA observations of continental earthquakes.Bull.Seism.Soc.Am.，2002，92（5）：1841－1846.

［32］ Venkataraman A，Kanamori H.Observational constraints on the fracture energy of subduction zone earthquakes.J.Geophys.Res.，2004，109：B05302，doi 10.1029／2003JB002549.

［33］ Hardebeck J L，Aron A.Earthquake stress drops and inferred fault strength on the Hayward fault，east San Francisco Bay，California.Bull.Seism.Soc.Am.，2009，99（3）：1801－1814.

［34］ McGarr A，Fletcher J B.Mapping apparent stress and energy radiation over fault zones of major earthquakes.Bull.Seism.Soc.Am.，2002，92（5）：1633－1646.

［35］ Abercrombie R E.Earthquake source scaling relationships from－1to 5 MLusing seismograms recorded at 2.5km depth.J.Geophys.Res.，1995，100（24）：15－24，36.

［36］ Bayrak Y，Yilmazturk A.Stress drop and classification of global earthquakes.／／Second Balkan Geophysical Congress and Exhibition.Istanbul，1999.

［37］ Shaw B E.Constant stress drop from small to great earthquakes in magnitude－area scaling.Bull.Seism.Soc.Am.，2009，99（2A）：871－875.

［38］ Moghaddam H，Fanaie N，Motazedian D.Estimation of stress drop for some large shallow earthquakes using stochastic point source and finite fault modeling.Transaction A：Civil Engineering，2010，17（3）：217－235，Sharif University of Technology，June 2010.

［39］ Ouillon G，Sornette D.Magnitude－dependent Omori law：Theory and empirical study.J.Geophys.Res.，2005，110：B04306，doi：10.1029／2004JB003311.

［40］ 徐錫偉，陳桂華，于貴華等.5.12汶川地震地表破裂基本參數的再論證及其構造內涵分析.地球物理學報，2010，53（10）：2321－2336.Xu X W，Chen G H，Yu G H，et al.Reevaluation of surface rupture parameters of the 5.12Wenchuan earthquake and its tectonic implication for Tibetan uplift.Chinese J.Geophys.（in Chinese），2010，53（10）：2321－2336.

［41］ 王衛民，趙連鋒，李娟等.四川汶川8.0級地震震源過程.地球物理學報，2008，51（5）：1403－1410.Wang W M，Zhao L F，Li J，et al.Rupture process of the Ms8.0Wenchuan earthquake of Sichuan，China.Chinese J.Geophys.（in Chinese），2008，51（5）：1403－1410.

［42］ 郭啟良，王成虎，馬洪生等.汶川Ms8.0級大震前后的水壓致裂原地應力測量.地球物理學報，2009，52（5）：1395－1401.Guo Q L，Wang C H，Ma H S，et al.In－situ hydro－fracture stress measurement before and after the Wenchuan Ms8.0 earthquake of China.Chinese J.Geophys.（in Chinese），2009，52（5）：1395－1401.

The spatio－temporal features of earthquake stress perturbation based on the simplified two－layer viscoelastic medium model

JIANG Hai－Kun1，WU Qiong1，SONG Jin1，LI Jin2，QU Jun－Hao3
1 China Earthquake Networks Center，Beijing100045，China
2 Institute of Earthquake Science，China Earthquake Administration，Beijing100036，China
3 Institute of Geology，China Earthquake Administration，Beijing100029，China

Based on the simplified two－layer viscoelastic medium model and its temporal characteristics of the deformation process，considering the joint action of the instantaneous elastic stress perturbation in the upper layer（more elastic）and the delayed and long－term load on upper layer due to the viscous relaxation deformation in lower layer（more viscous），the spatio－temporal variation of the earthquake stress perturbation has been studied.The results show that the stress perturbation increases quickly during a short time since the earthquake and then decays slowly for a long time.And when model parameters approach to real data more and more，the increasing anddecay process of the stress perturbation is slower，and the duration becomes gradually longer.In another word，the earthquake activity has a long－term‘memory’feature.Therefore，the longterm influence of stress perturbation could not be ignored in the study of earthquake activity or Coulomb stress changes.The stress perturbation has a limited acting range in space.It decreases obviously with distance inside the range，the decay is quick nearby the epicenter and is slow far away from the epicenter.The stress perturbation could be ignored outside the range.For the model parameters used in this paper，which approach to the real status for some extent，the effective acting range of the stress perturbation is about 2.5times of the linear fracture size of the earthquake.The stress perturbation increases gradually with the mainshock magnitude，for the assumed model parameters in this paper，it increases more quickly when magnitude is larger than M6.The relative error of stress perturbation，resulting from the measurement errors of the fracture size，is relational to the fracture size（magnitude）and epicenter distance，and there is no relationship with the time.The relative error increases with the epicenter distance，but its total influence on changing tendency and numerical range of the stress perturbation are very small，it tends to constant when distance is large enough.For earthquake with magnitude M6，M7and M8，the maximum relative errors of stress perturbation are smaller than 22%，30%and 38%.

Two－layer viscoelastic medium model，Earthquake stress perturbation，Duration，Acting range，Mainshock magnitude

10.6038／j.issn.0001－5733.2012.04.019

P315

2011－02－14，2011－09－07收修定稿

國家“十一五”科技支撐計劃項目（2008BAC38B03）資助.

蔣海昆，男，1964年生，博士，研究員.主要從事統計地震學研究.E－mail：jianghaikun＠sohu.com

蔣海昆，吳瓊，宋金等.雙層黏彈介質模型條件下地震應力擾動的時空特征.地球物理學報，2012，55（4）：1240－1248，

10.6038／j.issn.0001－5733.2012.04.019.

Jiang H K，Wu Q，Song J，et al.The spatio－temporal features of earthquake stress perturbation based on the simplified twolayer viscoelastic medium model.Chinese J.Geophys.（in Chinese），2012，55（4）：1240－1248，doi：10.6038／j.issn.0001－5733.2012.04.019.

（本文編輯 何 燕）