平行光入射時劈尖干涉誤差的定量分析

王 東 張 清 賈 虎

（安徽工業大學數理學院，安徽 馬鞍山 243002）

平行光入射時劈尖干涉誤差的定量分析

王 東 張 清 賈 虎

（安徽工業大學數理學院，安徽 馬鞍山 243002）

定量分析了平行光入射空氣劈尖和介質劈尖時，干涉條紋嚴格定域在劈尖上界面處時的條紋間距.數值計算表明對兩種劈尖作光線垂直入射垂直反射的近似處理時，空氣劈尖的誤差較大，但是小于4%.

劈尖干涉；誤差；條紋

1 引言

劈尖干涉是一種等厚干涉，在精密測量［1］、光學元件加工［2］、半導體工藝［3］等領域都有廣泛的應用.在劈尖干涉的很多應用中，由于劈尖尖角很小，都采用平行光垂直入射垂直反射的近似分析，近似認為劈尖干涉是分振幅干涉，干涉條紋定域在劈尖上表面.文獻［4］精確計算表明對平行光入射劈尖時的分振幅干涉，干涉條紋的定域中心位置難以確定，可以在劈尖上下界面附近，也可以在劈尖內部，干涉條紋空間坐標y與x呈復雜的函數關系.文獻［5］指出由于入射光具有一定發散角，條紋間距與平行光垂直入射時相比，條紋間距會隨膜厚增加而增大，這種干涉實際上與文獻［6］中點光源照射時的劈尖干涉相同，是分波前和分振幅相結合的一種干涉，干涉條紋就定域在劈尖的上表面.本文提出了一種劈尖干涉的新情況，即具有一定相干面積和相干長度的平行光入射劈尖時，干涉條紋也可嚴格定域在劈尖上表面，而且精確計算了平行光垂直入射時這種干涉的條紋間距，并比較了與常用的近似分析的條紋間距的差異.

2 劈尖干涉近似光路分析

如圖1所示，平行光由折射率為n1的介質中垂直入射折射率為n的劈尖.在劈尖上表面處入射光線一部分會反射，一部分會折射進入劈尖內部.如果劈尖的尖角很小，可以認為反射光線原路返回，折射光線垂直于劈尖下表面，折射光線經劈尖下表面反射后進入劈尖上表面在入射點與反射光線發生干涉［7］.干涉的光程差為

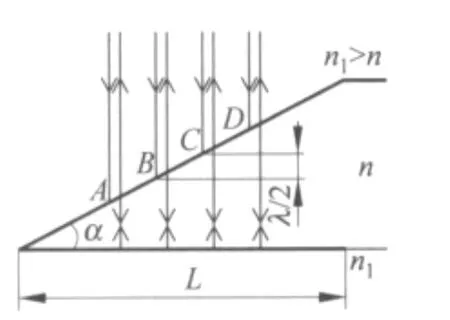
圖1 劈尖干涉近似光路

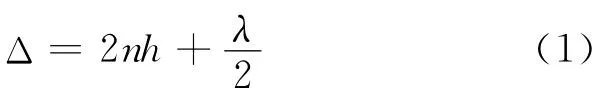
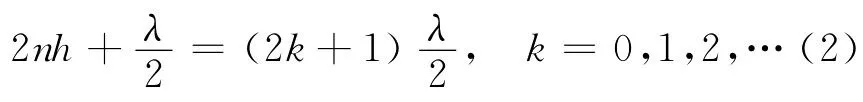
因此，干涉條紋是等間距的，為

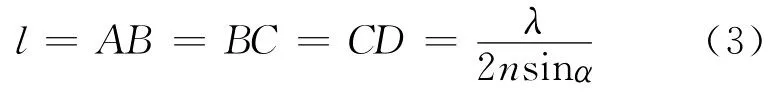
由此可得隨著劈尖尖角的增大，條紋間距會變小.

3 劈尖干涉光路精確分析

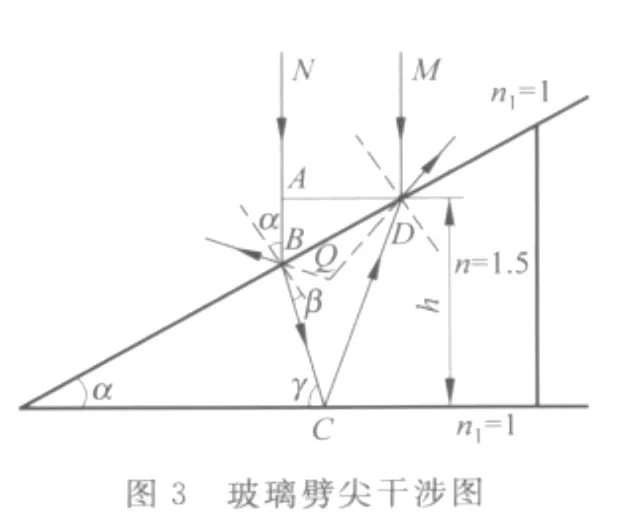
在劈尖干涉的近似分析中，折射進入劈尖內部的光線沒有按折射定律分析，導致分振幅干涉在光線入射點發生，實際上折射光線不可能回到入射點，因此上述近似分析是不夠精確的.圖2為平行光垂直入射空氣劈尖時干涉條紋在劈尖上界面時的精確光路.這種干涉應分兩種情況來討論.第一種情況是：入射光線MD在劈尖上表面D處分振幅，折射光線按照折射和反射定律經過劈尖下表面C點和上表面B點，在P點與反射光線發生干涉，這種干涉是完全的分振幅干涉.第二種情況是干涉條紋嚴格定域在劈尖表面的情況：入射光線MD折射進入劈尖，經劈尖下表面反射后，在B點與另一束光線NB的反射光線相遇而發生干涉.實際上理想的平行光是不存在的，這里的平行光可由截面積較大的激光束來代替，也可以將普通單色光源（如鈉光燈）放在較遠的位置，點光源發出的光線在劈尖附近如MD光線和ND光線可近似認為是平行的.所以這種干涉是分波前和分振幅相結合的等厚干涉.本文主要討論這種情況.

在界面B處干涉的光程差為

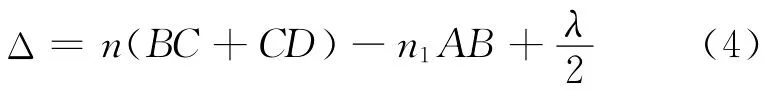
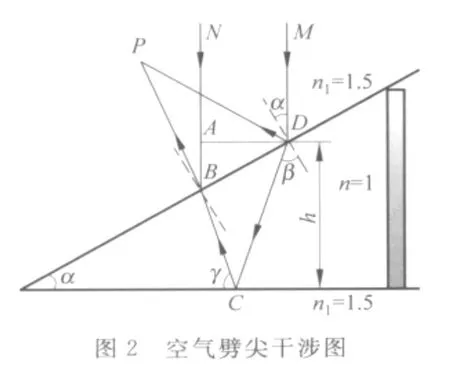
假設劈尖的尖角為α，入射光線MD在劈尖上表面處入射角為α，折射角為β.MD的折射光線與劈尖下表面的夾角為γ.β和γ均可由α、n和n1表示.由圖2可得

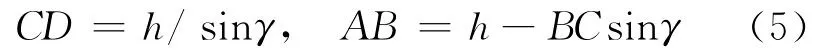
對三角形BDC，應用正弦定理可得

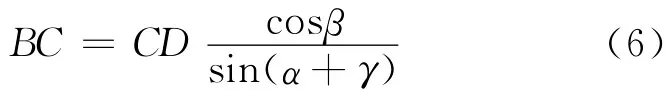
將式（5）和式（6）代入式（4），得干涉的光程差為

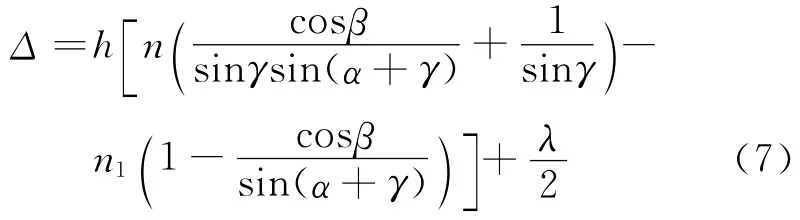
可以看出Δ與h成比例，因此干涉條紋是等間距的，條紋間距為

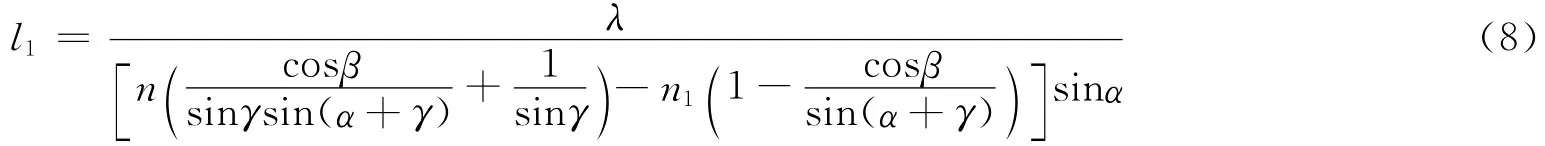
圖3為平行光入射玻璃劈尖時干涉的精確光路.從圖中可以看出，若當做分振幅干涉，這時干涉條文應定域在劈尖內部Q處.類似上面的分析可得在劈尖上表面處干涉的條紋間距為

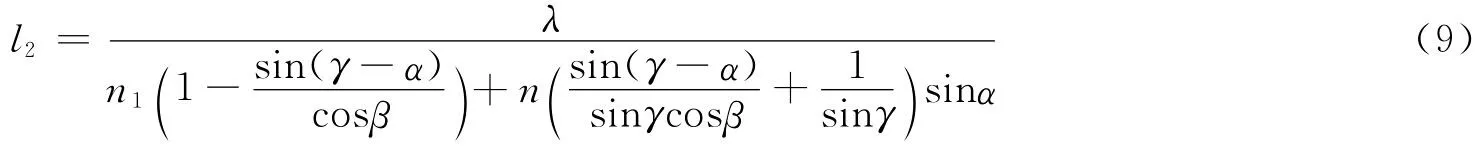
4 數值比較

假設入射的平行光為氦氖激光，波長為632.8nm，對圖2所示的空氣劈尖和圖3所示的介質劈尖，按照它們相應的條紋間距式（8）和式（9），可以分別計算在不同劈尖尖角下的條紋間距，再分別與近似式（3）作比較，可得空氣劈尖和介質劈尖條紋間距的精確值與近似值的差別隨劈尖尖角的變化關系分別如圖4和圖5所示.

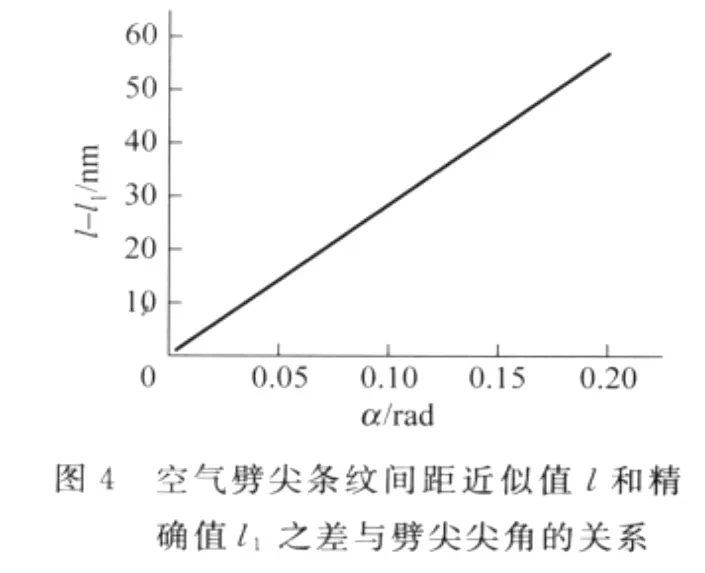
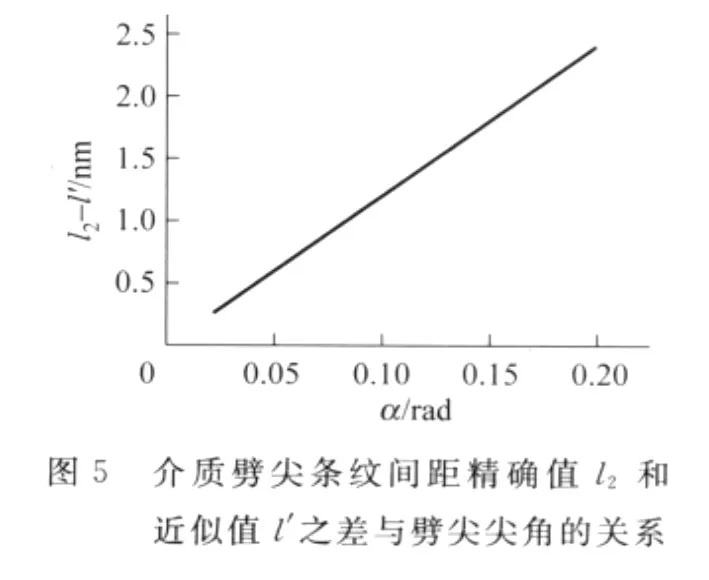
從圖4和圖5容易看出，兩種劈尖條紋間距的精確值與近似值之差都隨劈尖尖角增大而增大，空氣劈尖的精確值要比近似值小，介質劈尖的精確值要比近似值大.相同劈尖尖角下，空氣劈尖用近似公式（3）計算時引入的誤差要比介質劈尖大好多.但是即使對于空氣劈尖，在劈尖尖角達到0.19rad時，引入的條紋間距誤差也只有54nm，為條紋間距1.675μm的3.2%.

5 總結

本文采用具有一定相干面積的平行光做劈尖干涉，得出了干涉條紋嚴格在劈尖上界面時，空氣劈尖和玻璃劈尖條紋間距的表達式，結果表明干涉條紋也是等間距的.而且數值比較了精確計算與作光線垂直入射垂直反射時的近似分析的差別，結果表明空氣劈尖作近似分析時誤差比介質劈尖更大一些.本文的干涉方案避免了做分振幅干涉時條紋位置難以精確定位的問題，希望能夠在半導體器件設計中測定膜層厚度，標定光波長［8］等精密測量中得到應用.

［1］ 程玉寶，周慧鑫，劉上乾.一種激光探測與波長測定裝置的研究［J］.光電工程，2002，29（6）：25～27

［2］ 申仁智.空氣劈膜干涉條紋間距變化的判斷及其應用［J］.物理教學探討，2003，21（9）：20～21

［3］ Huo Fengwei，Kang Renke，Guo Dongming，Zhao Fuling，and Jin Zhuji.An Improved Angle Polishing Method for Measuring Subsurface Damage in Silicon Wafers.半導體學報，2006，27（3）：506～510

［4］ 劉金龍.劈尖干涉條紋定域的解析研究［J］.物理與工程，2008，18（4）：54～57

［5］ 劉香茹.劈尖等厚干涉實驗條紋不等間距的分析［J］.洛陽工學院學報，2000，21（3）：87～89

［6］ 趙凱華.光學（上冊）［M］.北京：北京大學出版社，1999.284～291

［7］ 馬文蔚.物理學教程.下冊［M］.2版.北京：高等教育出版社，2006.194～198

［8］ 吳海波，楊仕廣，程玉寶，焦 洋.一種基于劈尖干涉的激光波長測量裝置的研究［J］.激光與紅外，2009，39（8）：872～875

QUANTITATIVE ERROR ANALYSIS OF WEDGE INTERFERENCE WITH PARALLEL INCIDENT BEAM

Wang Dong Zhang Qing Jia Hu
（School of Mathematics and Physics，Anhui University of Technology，Ma'anshan，Anhui 243002）

The distance for two adjacent interference fringes in wedge stricken by parallel light is quantitatively analyzed for two kinds of wedges without the approximate treatment，in which the vertical light is reflected vertically.Numerical computation indicates the error for an air wedge is bigger than that for a glass wedge，but the error is still smaller than 4%.

wedge interference；error；fringe

2011－06－06；

2011－09－13）

王東（1980年出生），男，山西忻州人，講師，博士，主要從事量子光學與激光技術的研究及基礎物理的教學工作.