基于模糊綜合評判的智能行程時間預測算法

李慶奎，呂志平，葛智杰

（1.信息工程大學測繪學院，河南鄭州450052；2.解放軍66011部隊，北京102600；3.海軍出版社，天津塘沽300450）

近年來，針對行程時間預測，學者們提出了多種預測算法，如歷史趨勢法［1］、卡爾曼濾波算法［2］、時間序列法［3-4］、非參數回歸算法［5-6］、神經網絡模型［7-8］以及模糊回歸預測算法［9］等。這些算法都是基于歷史數據的預測算法，面對復雜多變的實際交通狀況，各算法的預測效果卻不能令人十分滿意。如歷史趨勢法不能解決非常規或突變的交通狀況；卡爾曼濾波算法在每次計算時都需調整權值，計算量大，預測結果延遲時間長；時間序列法在交通狀況發生急劇變化時，該算法在預測延遲方面暴露出明顯的不足［1］；由于非參數回歸算法需要對相鄰路段做復雜的調查，因此，應用于行程時間預測的非參數回歸模型屈指可數；神經網絡模型在數據不足時，會導致預測效果下降；模糊回歸模型由于未考慮相關路段信息和路段歷史流量信息對行程時間的影響，導致預測結果普遍偏小。為了得到更準確的行程時間預測結果，真實反映出道路的實時交通狀況，本文將模糊理論技術引入行程時間預測算法中，考慮交通流量、占有率等實時交通信息，提出了基于模糊綜合評判的智能行程時間預測算法。

1 模糊綜合評判的數學模型

模糊綜合評判是運用模糊方法對事物做出綜合評判，其過程是把評價目標看作由多種因素組成的因素集，再設定這些因素所能選取的評審等級，組成評語的評判集，分別求出每個因素對各個評審等級的模糊矩陣，然后根據各個因素在評價目標中的權重分配，通過模糊矩陣合成，求出評價的定量解值。模糊綜合評判的數學模型［10］為

B==(b1，b2，…，bn)

或

式中：“·”表示模糊運算，B=為被評對象的最終評價，A=為評價因素的權，R=為評價矩陣，其中rij表示第i個元素對第j種評語的隸屬度。此時得到的最終評價為模糊量，因此需將模糊量轉化成清晰量。清晰化方法可采用最大隸屬度法，加權平均法［11］等。

2 基于模糊綜合評判的行程時間預測模型

2.1 因素集、評判集及評判矩陣的確定

將行程時間定義為評判集V，并將行程時間劃分為極短、較短、一般、較長、極長5 個等級，分別用v1，v2，v3，v4，v5表示，記為V=。將影響行程時間的實時交通信息：交通流和占有率定義為因素集U，記為U={q，o} ，則評判集的每個等級都要用因素集的兩個個指標來描述。分別對交通流量q和占有率o進行評判得到模糊集R1=，R2=，于是可以確定評判集V和因素集U的評判矩陣：

評判矩陣R可由交通流量和占有率的隸屬度函數求得。

2.2 隸屬度函數的確定

隸屬度函數的確定問題是用模糊綜合評判解決具體問題的關鍵因素之一。隸屬度函數構造的合適與否，對判斷結果有著直接影響。三角形函數具有函數簡單、計算方便等特點。這里將交通流量和占有率數據構造成如下三角形隸屬度函數：

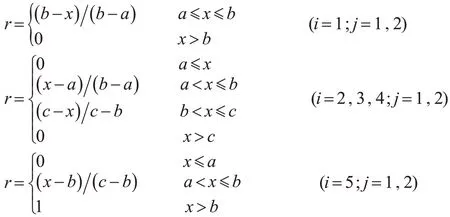
式中：a，b，c為待估參數（a，b為三角形隸屬函數三角形的“腳”；c為三角形隸屬函數三角形的“峰”）；i為評判集的等級個數；j為因素集個數。

2.3 清晰化方法的確定

在清晰化的過程中將行程時間的5 個等級：極短、較短、一般、較長、極長分別與區間［c0，c1］、［c1，c2］、［c2，c3］、［c3，c4］、［c4，c5］對應，清晰化方法采用加權平均法

式中：t為行程時間，ci為行程時間各等級的上限，μi(ci)為行程時間隸屬于各等級的隸屬度。

3 實驗驗證

算例數據采用深圳市的實測數據［11］，見表1。表1中的行程時間數據作為預測結果的檢驗數據。在此進行兩個方法的解算：

方法1 基于模糊回歸的行程時間預測算法［9］（TBFR）。

方法2 基于模糊綜合評判的智能行程時間預測算法（TBFCJ）。

在方法2中，占有率和交通流量的隸屬度函數參數的選擇見表2，因素權取A=（0.5，0.5）。在清晰化的過程中將行程時間的5個等級：極短、較短、一般、較長、極長分別與區間［0，40］，［40，70］，［70，100］，［100，140］，［140，185］對應，清晰化方法采用加權平均法。

表1 交通流量、占有率、行程時間數據Tab.1 Data of traffic volume，occupying rate and travel time

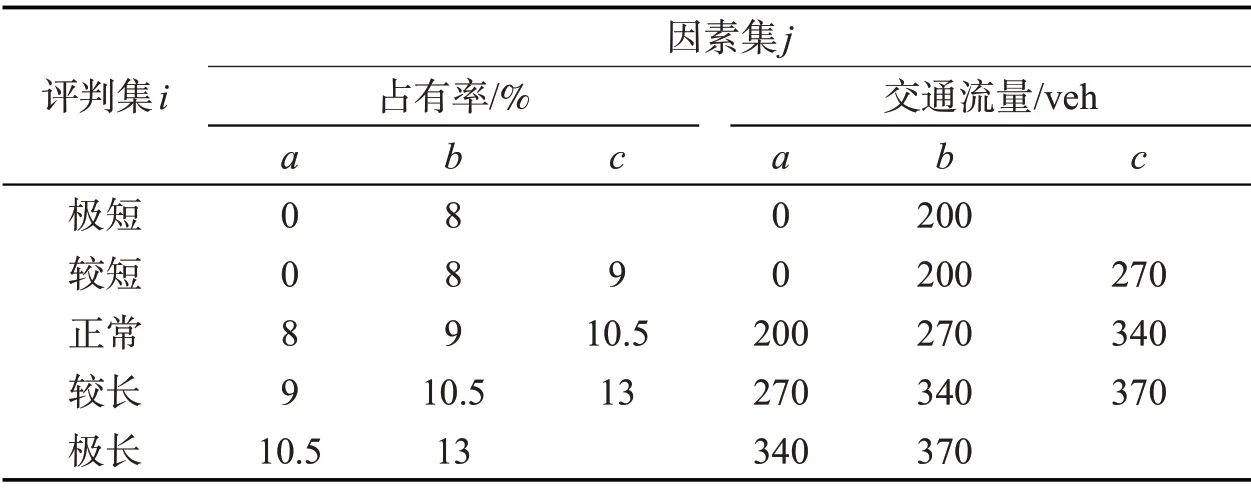
表2 隸屬度函數參數Tab.2 Parameters of membership functions

兩種行程時間預測算法的預測結果，其與行程時間真實值的對比如圖1和圖2。誤差分析見表3，絕對相對誤差見圖3和圖4。

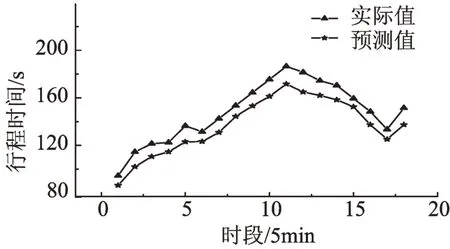
圖1 基于模糊回歸的行程時間預測結果Fig.1 Results of TBFR

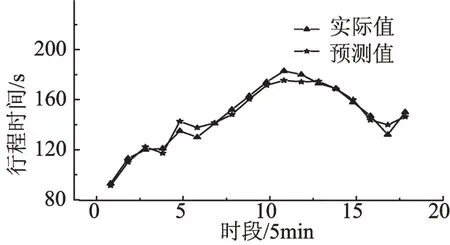
圖2 基于模糊綜合評判的智能行程時間預測結果Fig.2 Results of TBFCJ

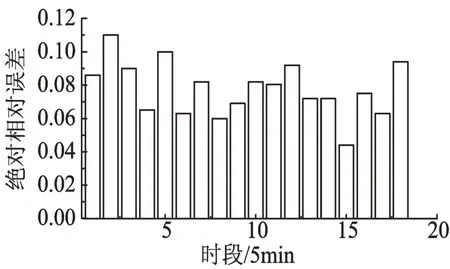
圖3 TBFR預測結果絕對相對誤差Fig.3 Absolute and relative errors of TBFR

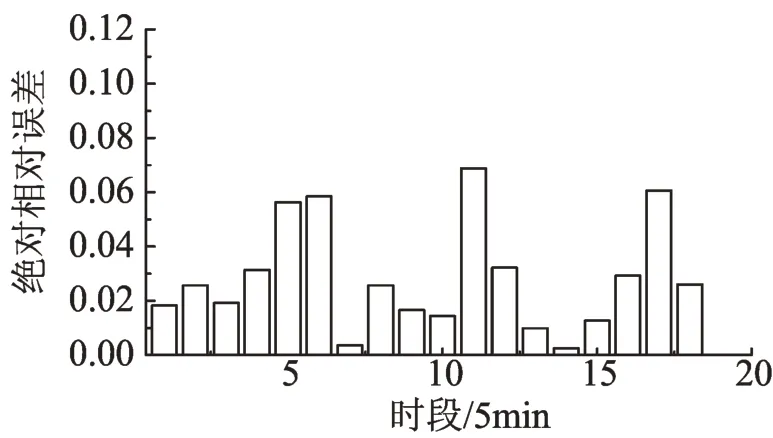
圖4 TBFCJ預測結果絕對相對誤差Fig.4 Absolute and relative errors of TBFCJ

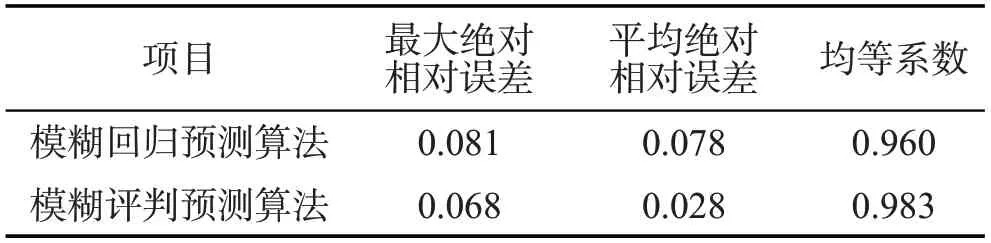
表3 誤差比較表Tab.3 Comparison of errors

從圖1和圖2兩種行程時間實際值與預測值的對比可以看出，兩種預測模型的行程時間預測值都能反映出行程時間實測值的變化趨勢。但從圖3、圖4 和表3 可以看出，模糊綜合評判預測算法的預測效果明顯好于模糊回歸預測算法，在最大絕對相對誤差、平均絕對相對誤差以及預測模型的預測值和實測值的曲線擬合程度方面都有明顯的提高（均等系數大于0.9說明擬合程度較好，均等系數越大擬合度越好）。

5 結論

影響行程時間預測的因素很多，特別是實時交通信息對行程時間預測的影響。各因素與行程時間之間構成了非常復雜的非線性關系，如果將這些因素用一個統一數據模型實現對行程時間的預測是相當困難的。模糊理論技術在處理非線性關系上具有巨大優勢，可以綜合考慮多種因素對行程時間預測的影響，合理分配各因素的權重，實現實時、準確的行程時間預測。本文在交通流量和占有率數據的基礎上，用模糊綜合評判的方法對行程時間實時預測，最后通過實例驗證了方法有效性、實用性和可行性。

［1］楊兆升.關于智能運輸系統的關鍵理論——綜合路徑行程時間預測的研究［J］.交通運輸工程學報，2001，1（1）：65-67.

［2］KUCHIPUDI，CHANDRA M，CHIEN，et al. Development of a hybrid model for dynamic Travel time prediction［C］//Trransponation Research Board，Annual Meeting 2002：35-39.

［3］ISHAK S，AL-DEEK H.Performance evaluation of short-term time-series traffic prediction model［J］.Joumal of Transportation Engineering，2002，128（6）：490-498.

［4］D’ANGELO M P，AL-DEEK H M，WANG M C.Travel-time prediction for freeway corridors［R］.Transportation Research Record，1999：184-191

［5］ROBINSON，STEVE J P.Modeling urban link travel-time using data from inductive loop detectors［C］//World Conference on Transport Research，2004：58-63.

［6］BAJWA S U I，CHUNG E AND KUWALLARA M. A travel time prediction method based on pattern matching technique［C］//21st ARRB and 11th REAAA conference，Cairns，Australia，2003：56-69.

［7］VAN LINT J W C.Reliable Travel Time Prediction for Freeways［M］.Delft University Press，Delft，The Netherlands，2004：121-122.

［8］PARK D AND RILETT L R.Forecasting multiple-period freeway link travel times using modular neural networks［R］.Transportation Research Record，1998：163-170.

［9］楊兆升，保麗霞，朱國華.基于Fuzzy回歸的快速路行程時間預測模型研究［J］.公路交通科技，2004，21（3）：78-81.

［10］胡寶清.模糊理論基礎［M］.武漢：武漢大學出版社，2010：73-74.

［11］劉金琨.智能控制［M］.2版.北京：電子工業出版社，2009：45-46.