Banach空間中的逼近問(wèn)題

常 青

（重慶師范大學(xué)數(shù)學(xué)學(xué)院，重慶 400047）

1 預(yù)備知識(shí)

設(shè)E是實(shí)Banach空間，C是非空閉凸集C?E，F(xiàn)(T)是映射T的公共不動(dòng)點(diǎn)集合.

定義1.1[2]設(shè)T:C→C是一個(gè)映象.

定義1.2[2]設(shè)E一個(gè)實(shí)Banach空間，C是E上的非空子集.

（1）映象P稱為從E到C的一個(gè)收縮映象，如果P2=P.

（2）稱C為E上的收縮核，如果存在一連續(xù)的收縮映象使得Px=x，?x∈C.

（3）特別地，稱C為E上的非擴(kuò)張收縮核，如果存在非擴(kuò)張收縮映象P:E→C使得Px=x，?x∈ C .

定義1.3[2]設(shè)E一個(gè)實(shí)Banach空間，C為E上的非空非擴(kuò)張收縮核，P為從E到C的非擴(kuò)張收縮映象.設(shè)T:E→C為非自映象.

（2）稱 T為非自漸近擬非擴(kuò)張映象，若F(T )≠? ，如果存在一序列{kn} ? [1,∞)且kn→ 1(n →∞)使得

（3）稱T是非自漸近非擴(kuò)張型映象，如果

（4）稱T為非自漸近擬非擴(kuò)張型映象，若F(T )≠?且滿足

注1 在C有界的情況下，由定義1.3可知：

（1）若T:C→T是一非自漸近非擴(kuò)張映象，則 T是一非自漸近非擴(kuò)張型映象；

（2）若T:C→T是一非自漸近擬非擴(kuò)張映象，則T是一非自漸近擬非擴(kuò)張型映象；

（3）若F(T)非空且T是非自漸近非擴(kuò)張型映象，則T是非自漸近擬非擴(kuò)張型映象.

定義1.4 設(shè)E為實(shí)Banach空間，C為E上的非空閉凸子集且為E上的收縮核，P:E→C的保核收縮映象， T1,T2,… ,TN為C到E上的非自漸近擬非擴(kuò)張型映象，?x1∈C，具有誤差的N步迭代序列{xn}定義如下：

要證明定理，需要引入如下的引理.

引理1.1[3]{an},{bn}為滿足下面條件的兩個(gè)非負(fù)實(shí)數(shù)列：

2 主要結(jié)果

其中 d(xn,F )為xn到F的距離.

證明（必要性）顯然.

（充分性）∵ T1,T2,… ,TN為C到E上的非自漸近擬非擴(kuò)張型映象，故?ε＞0，存在正整數(shù)n0使得當(dāng) n≥n0時(shí)，有

由于 {xn},｛ yni｝? C,i = 1,2,… ,N -1，對(duì)任意n≥n0有

由（1）和（4）有

類似的我們也可證明：

由（6）和（7）我們有

由歸納法，可以證明對(duì)任意i=1，2，…，N-1

特別地，在（8）取i=N-1，有

因此，由（5）和(9)有

下證（1）所確定的序列{xn}是柯西列，事實(shí)上，對(duì) ?n≥ n0,? m ≥ 1,?p∈ F，從（10）有

因此對(duì)n≥n0，m≥1.

由p的任意性，有

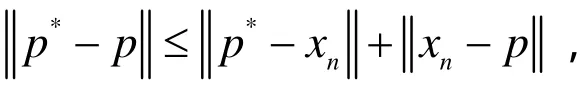
注：容易證明，若在定理2.1的 T1,T2,… ,TN:C→E是連續(xù)的，則 T1,T2,… ,TN的公共不動(dòng)點(diǎn)集F是閉集.

（1）ani+bni≤1，?n≥1，i=1，2，…，N；

證明：因?yàn)?T1,T2,… ,TN為C到E上的非自漸近擬非擴(kuò)張映象，有上述定義可知，它們是C到E上的非自漸近擬非擴(kuò)張型映象.由定理2.1的結(jié)論可知推論成立.

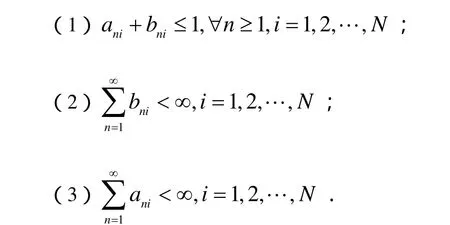
證明：因?yàn)?T1,T2,… ,TN為C到E上的非自漸近非擴(kuò)張映象，有上述定義可知，它們是C到E上的非自漸近擬非擴(kuò)張型映象.由定理2.1的結(jié)論可知推論成立.

[1]Goebel K, Kirk W A. A fixed point theorem for asymptotically nonexpansive mappings[J]. Proc Amer Math Soc, 1972(35).

[2]Y.X. Tian, S.S. Chang, J.L. Huang.On the approximation problem of common fixed points for a finite-family of non-self asymptotically quasi-nonexpansive-typemappings in Banach spaces[J]. 2007(53).

[3]N. Shahzad, A. Udomene. Approximating common fixed point of two asymptotically quasi-nonexpansive mappings in Banach spaces[J]. Fixed Point Theory and Applications,2006 (3).

[4]Ya.I.Alber,C.E.Chidume,H.Zegeye.Approxim ating of total asymptotically nonexpansive mappings[J]. Fixed Point Theory and Applications,2006 (1).

[5]鄭蓮.非擴(kuò)張映象的一個(gè)新的迭代過(guò)程[J].長(zhǎng)江師范學(xué)院學(xué)報(bào)，2002（5）.