具有Hassell-Varley型功能性反應的捕食系統周期性

王 莉

（重慶師范大學數學學院，重慶 400047）

隨著科學技術的發展，人們發現脈沖微分方程較之不帶脈沖的微分方程更能真實地反映自然界發展過程中的某種現象，科學和技術的許多領域如理論物理、機械、種群動力系統、流行病動力系統、工業控制、生物、技術經濟等許多方面的變化規律都可以用脈沖微分方程來刻畫或描述，這使得脈沖微分方程的研究更有意義.在實際過程中，生態學模型的參數在特定的時間會發生突變，所以本章考慮具有脈沖效應和時變時滯的Hassell-Varley型功能性反應捕食系統，具有一定的生態意義和現實意義.

考慮下面的具有脈沖效應和時變時滯的Hassell-Varley型功能反應的捕食系統：

其中n∈z+，0＜δ＜1，x(t),y(t)表示種群中食餌，捕食者隨時間變化過程，k，α，r，β，γ分別表示食餌捕獲率，半飽和常數，內稟增長率，捕食者的死亡率和食餌生物量轉化為捕食者生物量的轉化率；δ稱為H-V系數.

t＝tn為定期收獲或投放時刻（脈沖時刻），cn，dn分別為食餌，捕食者的收獲率或投放率，不失一般生物意義，本章中總是假設：

（i）脈沖時刻｛tn｝,n∈z+滿足t0＝0＜t1＜Λ＜tn＜Λ；

（ii）存在正數ω＞0和正整數p，使得tn+p＝tn＋ω, cn+p＝cn, dn+p＝dn,cn,dn＞-1；

（iii）函數 r:R ?R,k,b ,α,β,γ,τi:R? R+是連續ω-周期的（i=1,2,3）.

在（i）-（iii）條件下， R+2是系統(1)的不變集.

為方便，設J?R，記 PC ={g:J →R2|g(t)在t≠tk處連續，在t=tk處左連續右極限存在，k ∈ Z+}.

對ω-周期函數g(t)和ω-周期序列｛cn｝｛dn｝，我們采用下列記號：

下面給出本章中需要用到的一些引理：

引理1 （延拓定理[1]）設L是指標為零的Fredholm映射，N在上是L-緊的

假設（a）對任意λ∈(0，1)，方程 Lx=λN x的解滿足x??Ω；

（b）對任意的 x ∈?Ω∩ KerL,QNx ≠0,，而且deg｛ JQ N,Ω ∩KerL,0｝≠0

下面利用重合度理論得到了系統（1）正周期解存在的充分條件.

定理1 如果系統（1）的參數滿足：

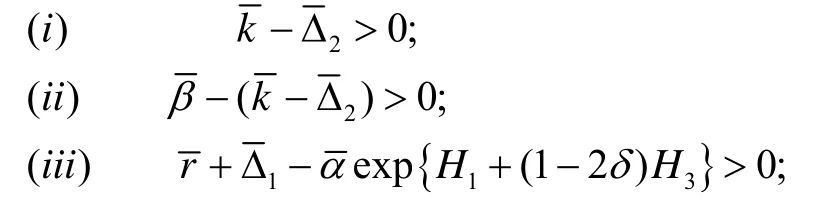
其中

則系統（1）至少存在一個ω-正周期解.

證明：作變換x（t）= exp｛ u（t）｝，y（t）= exp｛v （t）｝，則系統（1）變為

其中

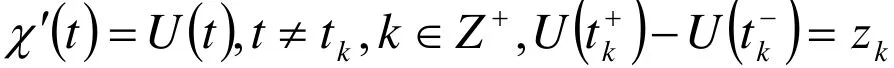
對任意 λ∈ （0,1）由算子方程 LU=λN U，U∈X，有

對（2）從0到ω積分，得

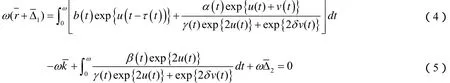
從（3）～（5）知，

由于（u,v）T∈ X ，那么存在 ξi,ηi∈［0,ω ］, i=1,2,使得

由（4）（8）知，

則有

于是，利用（6）（9）有

同樣地，由（5）（8）（10）知

則

故而

則

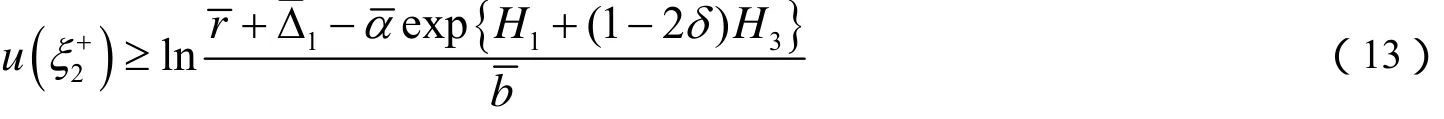
則

則有

則

同樣地，由（5）（17）及0 ＜ γ(t) ≤ 1，（γ(t)為食餌生物量轉化為捕食者生物量的轉化率，故范圍在0到1之間）及定理2知，

則

則有

至此，對任意的 λ∈ （0,1），我們已對算子方程 LU=λN U 的解 u（t）,v （t）作了估計：H2≤u（t）≤ H1,H4≤v（t）≤H3,其中 H1,H2,H3,H4與λ無關.

現在我們取

由上估計，對任何 λ∈（0,1）,L U =λNU 的任意解都滿足x??Ω，即引理1的第1個條件成立.為驗證第2個條件，我們現在考慮關于（u , v ）T∈ R2的代數方程組：

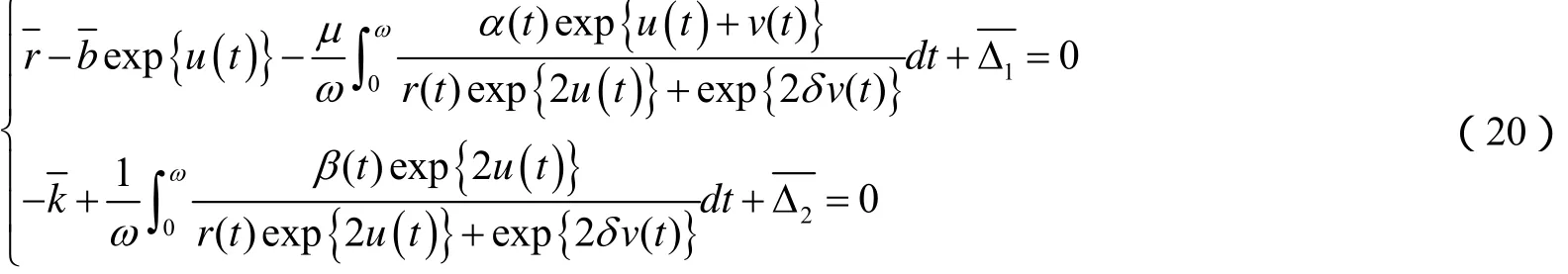
這里μ∈[0,1]，類似以上的估計過程，易證對于任意μ∈[0,1]，代數方程(20)的解（U,V）T有界，事實上，它也滿足估計：

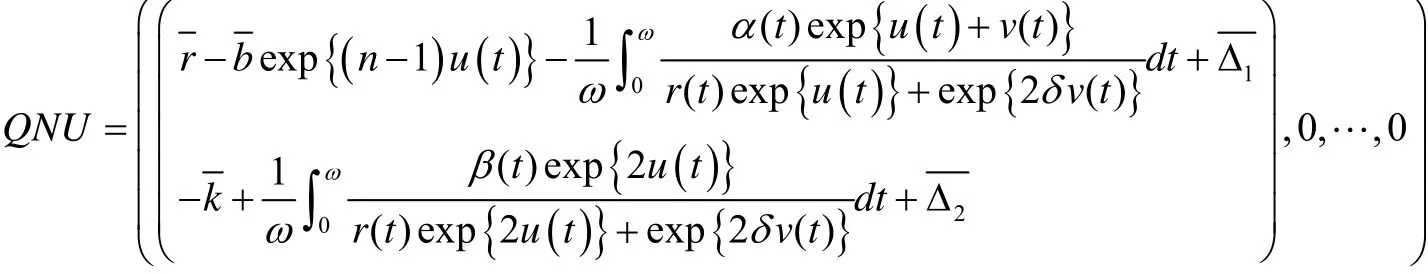
由（9），對任意的 U∈?Ω∩ KerL,都有 QNU ≠0.為了計算Brouwer度，構造同構變換G（μ,U ）= μQNU+（1-μ）H （U）,μ∈［0,1］.這里， U= （u,t ）T且

從（21）可以看出，對任意 U∈?Ω∩ KerL 和 μ∈ ［0,1］,都有G（μ,U ）≠0.由假設， H （U）=0都有唯一 解 . 由 Im Q= KerL,取 J=I,并 利 用 同 構 不 變 的 性 質deg ｛JQN ,Ω ∩KerL, 0｝ =deg ｛Q N ,Ω ∩KerL, 0｝ =deg ｛H ,Ω ∩KerL,0｝ ≠0.因此，我們驗證了引理1的所有條件.從而 LU= NU在DomL ∩上至少有一解 （U*（t）,V*（t））T，且也是方程（2）的周期解. （x*（ t）,y*（t））T= （exp｛u*（t）｝,exp｛v*（t）｝）T也是方程（1）的正周期解.證畢.

[1] Gaines R.E.and Mawhin J.L.,Coincidence degree and nonlinear differential equations[M].Springer-Verlag,Berlin,1977.

[2] Hassell M P. Varely G C.New inductive population model for insect parasites and its bearing on biological control[J].Nature,1969,223:1133-1137.

[3] Arediti R and Ginzburg L.R.Coupling in predator-prey dynamics:Ratio-dependence,J[J].Theoretical Biology,1989,139:311-326.

[4]溫紹雄，范猛.離散Hassell-Varley型功能性反應的捕食者-食餌系統周期解的存在性[J].東北師大學報：自然科學版，2011（1）.

[5]羅廷友，劉啟寬，李映輝.一類食餌-捕食系統的定性分析[J].四川理工學院學報：自然科學版，2011（2）.

[6]劉秀湘，黃立宏.離散Hassell-Varley型功能性反應系統的正周期解[J].數學的實踐與認識，2009（12）.

[7]楊志春.具有脈沖和Holling III類功能反應的捕食系統的持續生存和周期解[J].生物數學學報，2004（4）.

[8]王守和，李常菊.一種非自治捕食鏈系統的持久性與全局吸引性[J].三峽大學學報：自然科學版，2009（6）.

[9]楊志春，徐道義.具有反饋控制和無窮分布時滯的脈沖型競爭系統的正周期解及其穩定性[J].應用數學學報，2009（1）.

[10]陳巧靈，栗永安，姜彩玉.具有階段結構與功能反應的捕食-食餌系統的最優捕獲策略[J].重慶工學院學報：自然科學版，2008（11）.

[11]樊曉明，王志剛，羅振江.具功能反應的投放率的非自治捕食-食餌系統的周期解和持久性[J].數學的實踐與認識，2008（9）.

[12]范猛，王克.多種群生態競爭系統周期正解的存在性和全局吸引性[J].數學學報，2000（1）.