車載多管火箭炮發射系統基座的輕量化

林國問，馬大為，朱孫科

（南京理工大學 機械工程學院，南京210094）

基座是車載多管火箭炮發射時的依托平臺，它起著連接火箭炮轉塔上部分與運載體的作用.在火箭炮發射時，會將發射時產生的燃氣流沖擊力、火箭炮自身的重力等載荷傳遞給運載體，其性能好壞直接影響著全炮的安全可靠性和射擊時的精準性.隨著現代戰爭對武器系統機動性提出的要求，輕量化成為武器系統的發展方向之一.

研究武器系統輕量化的方法很多，其中包括采用輕質高強材料、合理的簡化結構及通過優化方法找尋結構合理的傳力路徑進行結構優化等.結構拓撲優化可以找尋結構合理的傳力路徑，它主要以提高結構性能或使結構輕量化為目標，在國際上，已經廣泛地應用于飛機、汽車及其他機械產品的開發中，取得了很好的效果[1].目前結構拓撲優化的主要對象是連續變量的結構優化，比較成熟的方法[2，3]包括均勻化方法、變密度法和漸進結構優化方法等.

文中利用變密度法對基座的結構進行輕量化研究.對車載多管火箭炮發射時常用的典型射擊工況，即最大射角下的基座進行拓撲優化，獲得了約束條件下基座材料的最佳分布形式，結合工程要求建立了優化后的基座模型，并進行了剛強度校核和動力學響應分析，通過應用比剛度結構效能對優化前后的基座剛度進行了對比分析和炮口響應的研究，結果顯示，用拓撲優化可以減輕基座的質量，同時對動態響應影響不大.優化方法可以應用于該產品的設計中，同時，對同類的產品結構設計具有參考意義.

1 拓撲優化的基本理論

拓撲優化設計技術能夠在給定的設計空間內找出最佳的材料分布，拓撲優化能夠大大改善結構的性能和減小結構的質量.連續體結構拓撲優化常用的方法是均勻化法和變密度法.變密度法[4～6]以連續變量的密度函數形式表述單元相對密度與材料彈性模量之間的對應關系，這種方法基于各向同性材料，不需引入微結構和附加的均勻化過程，程序實現簡單，計算效率高，因此，本文采用變密度法對基座結構進行拓撲優化研究.

基于變密度法的拓撲優化理論[7]，其數學模型如下：

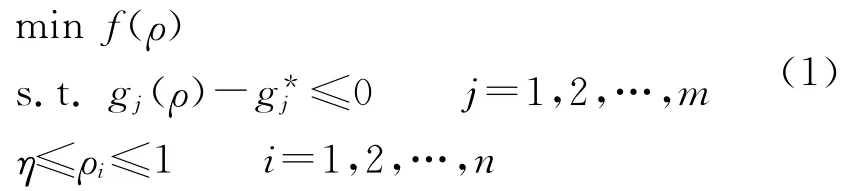
式中，f（ρ）為目標函數；ρi為單元的密度；gj（ρ）為第j個約束為約束上限；m為約束數；η是使剛度矩陣非奇異的極小正數，通常取為0.001[2]；n為總的單元數.

拓撲優化是一種0～1變量的復合優化問題，但在優化過程中有時會出現一種包含中間密度的情形，通常在優化控制中主要通過引入懲罰因子對其加以避免.懲罰因子在拓撲優化過程中能夠有效地對中間密度值進行控制，使優化結構盡可能地呈現0和1的結構形式，從而使優化后的結構避免中間材料的出現.因此，為了獲得0/1的密度分布，本文優化時采用冪指數公式[2，8]：

式中，Ki（ρ）和Ki分別為單元的懲罰剛度矩陣和真實剛度矩陣；p為懲罰因子，通常取2～4[9].

在結構拓撲優化問題中，棋盤格現象和網格依賴性是2個常見的數值不穩定問題.文中優化時采用文獻[2，10]提出的最小成員尺寸控制（MMS），這有效地克服了拓撲優化過程中的棋盤格現象和網格依賴性.MMS理論可以抽象成：

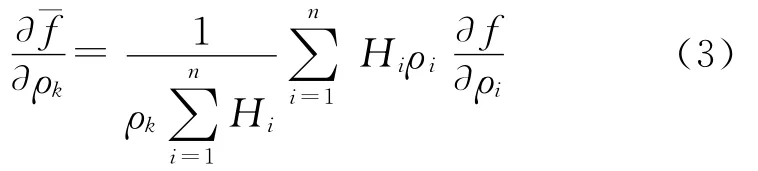
式中，網格獨立加權因子Hi可表示為

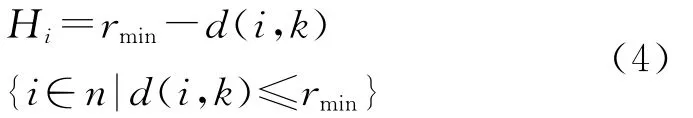
式中，rmin為預設最小成員的半徑；單元i和單元k為相鄰的單元，d（i，k）為單元i和單元k之間的距離.

2 基座的拓撲優化

2.1 優化幾何模型

基座結構的幾何模型如圖1所示，結構有承載面1，圓柱連接面2，加強筋3及與運載體固定面4.基座各部分之間主要通過焊接而成，通常焊縫及其熱影響區的強度及剛性會比母材高，所以建模時將焊縫在幾何上連接在一起處理，這與實際情況差別不大[2].由于基座結構在2個方向的尺寸明顯大于第三個方向的尺寸，因此，在進行有限元分析時采用殼單元建立有限元模型，如圖2所示.在圖2中的特征點1位置，需要滿足相關的設計和制造約束，在此忽略其變形，采用剛性單元來模擬，在特征點1位置施加載荷.

基座是通過鋼板焊接而成，其設計要求為承載面在第一組4發彈齊射時，在巨大載荷作用下，承載面垂直方向的位移不大于1mm.

根據動力學計算，當發射角在最大射角時，第一組4發彈齊射時，承載面在垂直方向的位移為0.67mm.發射關鍵部位的位移小于設計要求，因此，有進行結構優化的余量存在.在基座進行拓撲優化時，應使關鍵部位的位移在設計的指定值范圍內，而整體質量盡量小，從而達到輕量化的目的.

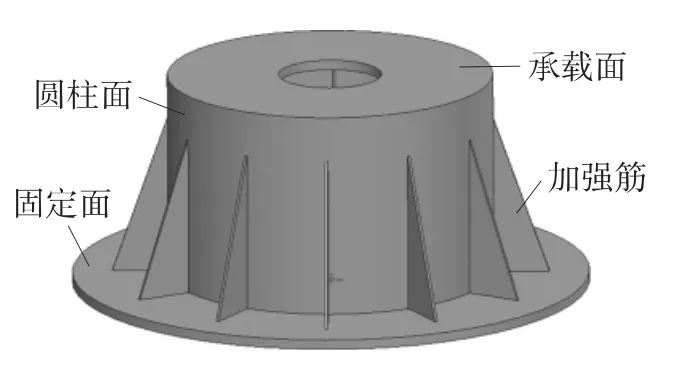
圖1 基座的幾何模型

圖2 基座的有限元模型

2.2 優化模型設置

文中對基座優化模型設置為：

①以基座結構的質量最小化為目標函數；

②以承載面垂直方向允許的最大位移，即在第一組4發彈發射時，基座上表面在垂直方向的位移不大于1mm作為約束條件；

③以基座的相對單元密度為設計變量.

2.3 拓撲優化結果

本文借助Hyperworks中的Optistruct優化模塊[11]優化基座結構，經過12次的迭代達到收斂，如圖3所示，ms為結構質量，N為優化迭代次數.

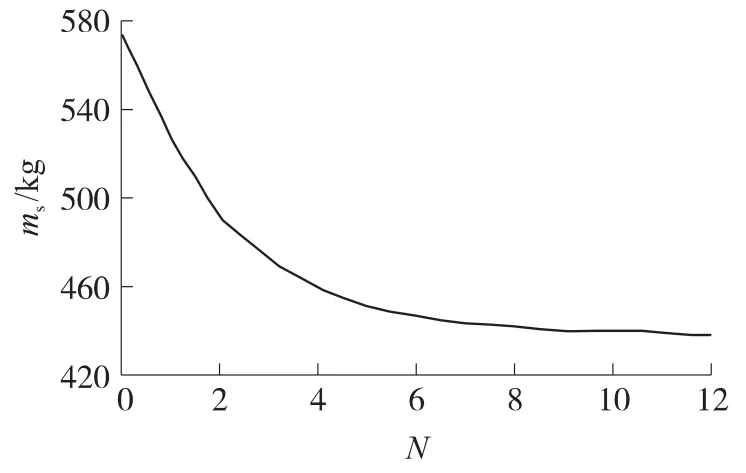
圖3 質量與迭代次數關系曲線

從圖3可以看出，基座在前7次的迭代過程中質量大幅度地減小，到第8次迭代后計算基本收斂，質量不再減小，這說明基座初始結構中存在大量不起主要承載的材料.

結合基座的優化結果并考慮制造的可行性以及結構的對稱性和美觀性，同時以盡可能地減輕質量為目的，在基座圓柱面上開一個長方形孔以及上下各一個半圓孔，為了避免應力集中造成結構的損壞，結構的孔邊界要求盡量圓滑，同時將優化中刪除的加強筋予以加上，從而既使結構達到了美觀和對稱，又使結構的剛強度有所富裕和質量盡可能減小.拓撲優化結果如圖4所示，優化后的幾何模型如圖5所示.

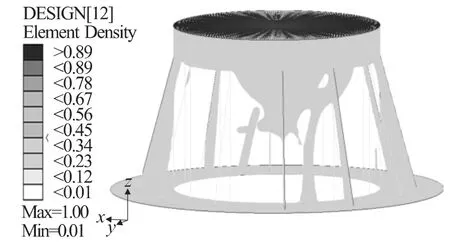
圖4 基座優化結果

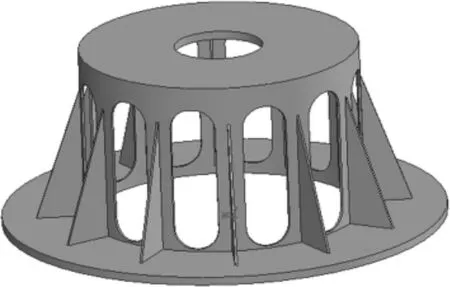
圖5 基座優化后的幾何模型

3 結果分析

3.1 剛強度分析

將優化后的基座結構進行剛強度校核，優化前后的分析參數分別如表1所示，其中σ和s分別為基座的最大應力和最大位移；β為比剛度結構效能.

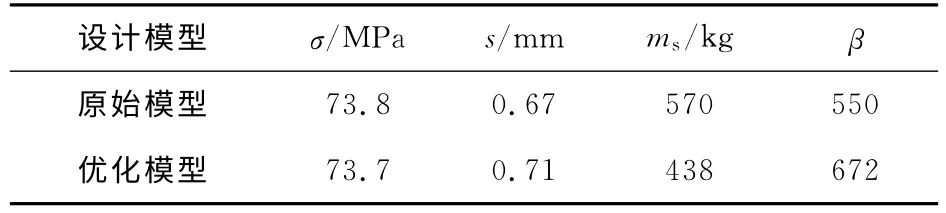
表1 優化前后的參數

從表1中可知，盡管優化后的位移值比優化前有所增大，但都在設計的范圍內.優化前后應力基本保持不變，均遠小于材料的屈服極限.對于多管火箭炮來說，基座的結構相比于強度，高剛度在結構設計時顯得更重要.因此，本文利用文獻[12]中提出的比剛度結構效能β，對基座進行了比剛度分析.

式中，E為材料的彈性模量.

效能值越大，說明結構具有越高的單位質量剛度[2].從表1中可以看出，優化后的基座質量減小，而且優化后的比剛度結構效能大于優化前，說明優化后基座結構的單位質量的剛度裕度得到了改善.

3.2 動力學響應分析

將優化后的基座重新建模，并用于整炮動態響應分析，動力學仿真分析時，采用的是4－2發射方式，即先齊發第一組4發彈，待4發彈出管口且飛一段距離后在齊發第二組2發彈.彈性模量為210GPa，泊松比為0.3，密度為7 850kg/m3.圖6為優化前后的整炮網格模型；圖7為炮口響應曲線，圖中，v1，v2分別為炮口偏航速度和俯仰速度；ω1和ω2分別為炮口偏航角速度和俯仰角速度.

圖6 優化前后整炮網格模型

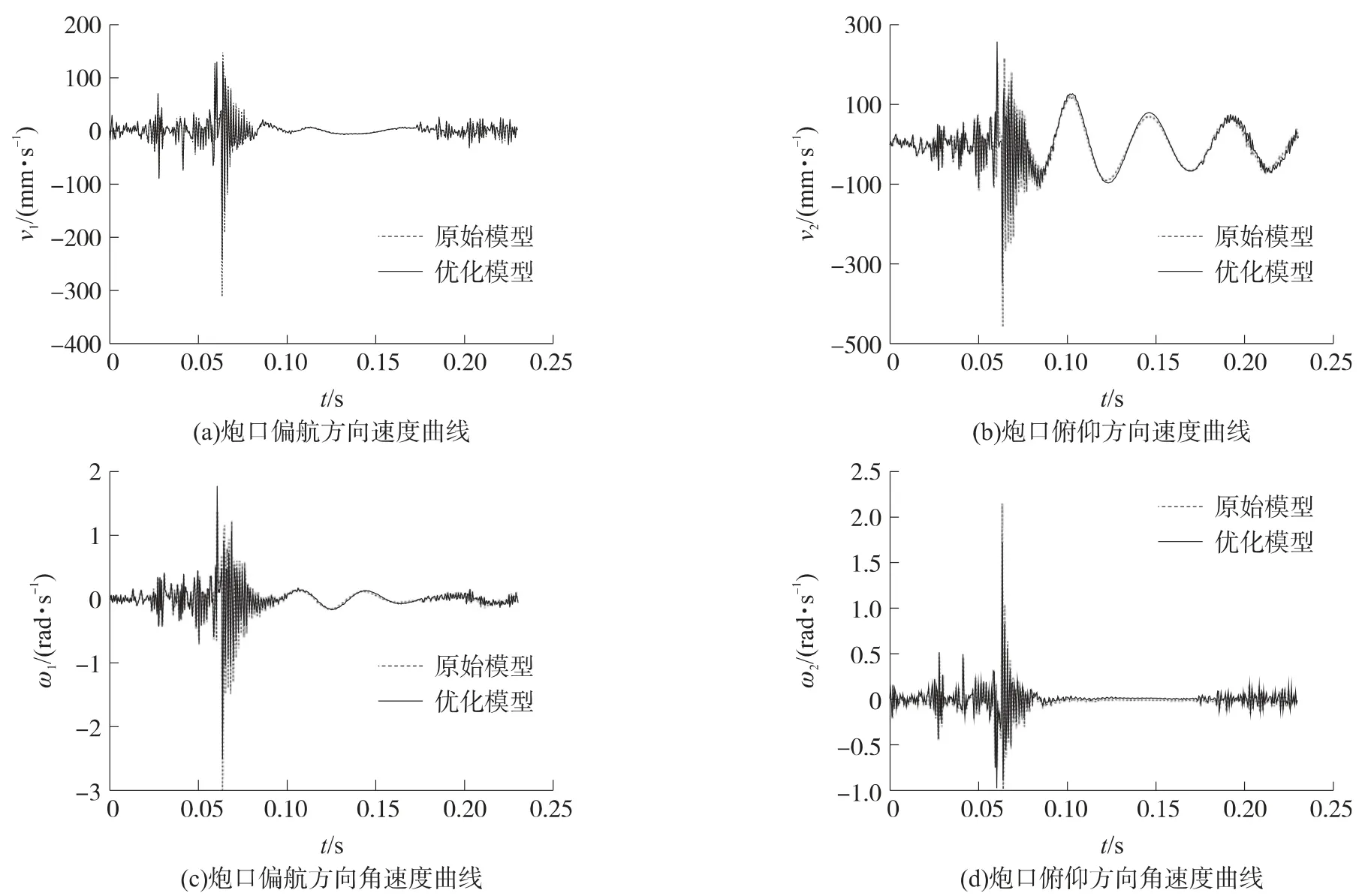
圖7 炮口響應分析

圖7中曲線出現2次波動，主要是由2組彈先后發射所致，虛線表示基座采用原始結構，即原始模型；實線表示基座采用優化后的結構，即優化模型.從圖7中可以看出，在整炮的動態響應分析中，優化前的基座和優化后的基座所產生的炮口響應變化不大，基本在一個數量級.因此，優化后的基座在滿足剛強度后，在整炮的動力學響應分析中也能滿足要求，對多管火箭炮的性能影響基本可以忽略.這說明對基座拓撲優化是可行的.

4 結論

文中針對車載多管火箭炮發射系統基座的輕量化問題，進行了基于變密度法的結構拓撲優化.對基座結構進行剛強度校核及動力學響應研究，結果顯示，剛強度滿足設計要求，優化前后的炮口響應無明顯變化.優化設計后基座的質量得到了有效的減輕，減重達23%.相比于初始結構，優化后基座的效能值有所增加，表明基座的優化方案是有效的.該方法也可用于多管火箭炮其他部件的拓撲優化設計和輕量化研究.

[1]張勝蘭，鄭冬黎，郝琪，等.基于 Hyperworks的結構優化設計技術[M].北京：機械工業出版社，2007.ZHANG Sheng－lan，ZHENG Dong－li，HAO Qi，et al.Structural optimization design based on hyperworks[M].Beijing：China Machine Press，2007.（in Chinese）

[2]朱孫科，馬大為，何勇，等.基于動力學仿真的艦炮基座結構拓撲優化設計[J].系統仿真學報，2007，21（20）：6 650－6 657.ZHU Sun－ke，MA Da－wei，HE Yong，et al.Topology optimization of naval gun seat based on dynamic simulation[J].Journal of System Simulation，2009，21（20）：6 650－6 657.（in Chinese）

[3]劉加光，陳義保，羅震，等.連續體結構的模糊多目標拓撲優化設計方法研究[J].系統仿真學報，2007，19（5）：1 095－1 099.LIU Jia－guang，CHEN Yi－bao，LUO Zhen，et al.Fuzzy multiobjective topology optimization of continuum strutures[J].Journal of System Simulation，2007，19（5）：1 095－1 099.（in Chinese）

[4]湯穎穎.基于變密度法的連續體拓撲優化設計[D].西安：長安大學，2008.TANG Ying－ying.Research on topology optimization methods of continuum structure based on variable density method[D].Xi’an：Chang’an University，2008.（in Chinese）

[5]劉曉梅.某特種車輛艙體結構的有限元分析與優化[D].南京：南京理工大學，2007.LIU Xiao－mei.Finite element analysis and optimization of one special vehicle cabin[D].Nanjing：Nanjing University of Science and Technology，2007.（in Chinese）

[6]崔明濤.不確定性連續體結構拓撲優化和柔性機構設計研究[D].西安：西安電子科技大學，2006.CUI Ming－tao.Research on topology optimization of continuum structures and design of compliant mechanisms with uncertainty[D].Xi’an：Xidian University，2006.（in Chinese）

[7]BENDSOE M P，SIGMUND O.Topology optimization theory，methods and application[M].New York，USA：Springer Press，2003.

[8]ZHOU M，PAGALDIPTI N，THOMAS H L，et al.An integrated approach to topology，sizing and shape optimization[J].Structural Multidisciplinary Optimization，2004，26（5）：308－317.

[9]ZHOU M，FLEURY R，SHYY Y K，et al.Progress in topology optimization with manufacturing constraints[C].Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary A－nalysis and Optimization.USA：AIAA，2002：1－8.

[10]ZHOU M，SHYY Y K，THOMAS H L.Checkerboard and minimum member size control in topology optimization[J].Structural Multidisciplinary Optimization，2001，21 （2）：152－158.

[11]于開平，周傳月，譚惠豐.HyperMesh從入門到精通[M].北京：科學出版社，2005.YU Kai－ping，ZHOU Chuan－yue，TAN Hui－feng.HyperMesh：from intrudction to master[M].Beijing：Science Press，2005.（in Chinese）

[12]岑海棠.結構仿生理論、輕質零件結構仿生設計及RP工藝驗證[D].北京：北京航空航天大學，2004.CEN Hai－tang.Study on structural bionics theory，lightweight structure bionics design and rapid prototyping testing[D].Beijing：Beijing University of Aeronautics Engineering and Astronautics，2004.（in Chinese）