二維正方晶格光子晶體的帶隙研究*

袁秀娟，潘 鳴，曹 威

(1.杭州電子科技大學電子學院，杭州310018;2.中國電子科技集團公司第五十研究總體部，上海200063;3.西安外事學院工學院，西安710077)

太赫茲(THz，1 THz=1012Hz)這一概念是Fleming在1974年提出來的，泛指頻率在0.1 THz～10 THz這一波段內的電磁波［1］。該段電磁波，在電磁波譜上位于微波和紅外波之間，被稱為亞毫米波和遠紅外波。1 THz光子的等效溫度為48 K，因此自然界廣泛存在THz射線。由于THz的低能性，高透性，以及其豐富的指紋譜性［2-4］，THz已經引起了科學界的廣泛關注［5］。THz特性的研究及其開發利用與各種操控THz波的光學器件密不可分，THz研究的不斷發展對這些器件提出了很大的需求。在這種情況下，“光子晶體”這一特殊材料應運而生。光子晶體的概念，于1987年由S.John和E.Yablonovitch分別提出，是指由兩種或兩種以上介質周期排列所構成的人造晶體［6-7］。光子晶體最重要的特征就是具有光子禁帶，凡是頻率落在禁帶中的光，不論其波矢和偏振方向如何，都會被嚴格禁止傳播。利用這一特性可以將其應用于THz波段的電磁波傳輸和濾波，且具有色散小、損耗低等優點，可以制作出多種品質優良的THz器件。

本文利用平面波展開法［8-11］(PWM)分析研究了正方晶格THz光子晶體的禁帶特性。平面波展開法主要是將電磁場在倒格矢空間以平面波疊加的形式展開，將Maxwell方程化成一個本征方程，然后求解本征值即可得到傳播光子的本征頻率，從而獲得光子晶體的光子禁帶。

1 理論和計算方法

THz波在二維正方晶格光子晶體中的傳輸特性可用Maxwell方程來描述。傳播方程如下:

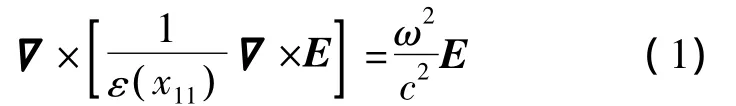
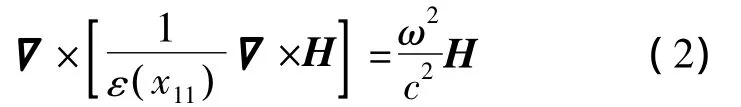
圖1(a)為介電常數為εa的介質圓柱嵌在介電常數為εb中材料中所構成的二維正方晶格光子晶體的截面圖。介質柱半徑為r，晶格常數為a。圖2為正方晶格的第1 Brilliouin區。二維光子晶體中，入射電磁波可以分解為E偏振和H偏振，即電場平行于介質柱的TM模和磁場平行于介質柱的TE模。

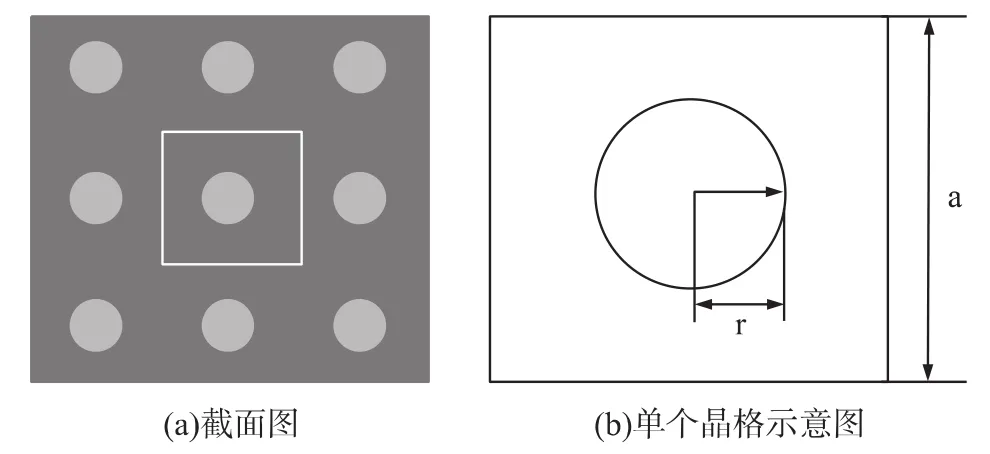
圖1 二維正方晶格光子晶體

由二維光子晶體的周期性，可以把ε-1(x11)，H3(x11，ω)展開成傅里葉級數

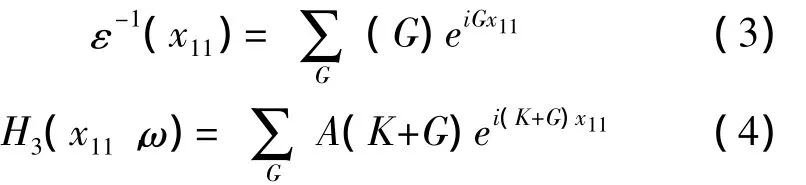
其中K是被限制在第1 Brillouin區域的波矢量。

首先考慮H偏振，此時H和E可寫成:

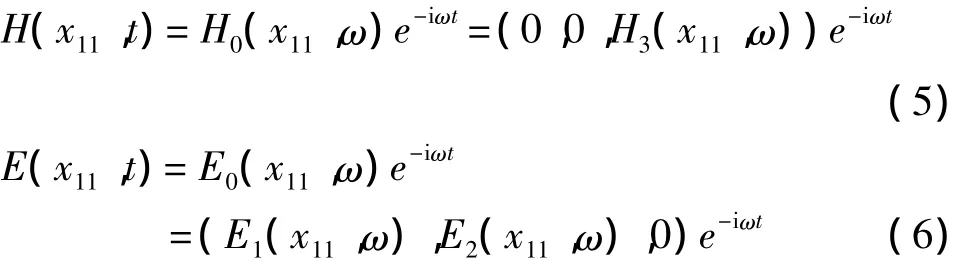
其中x11為坐標軸所構成的平面上的矢量。把式(5)和式(6)代入式(2)，消去E1和E2，可以得到H3的表達式:

再把式(3)和式(4)代入式(7)可得:

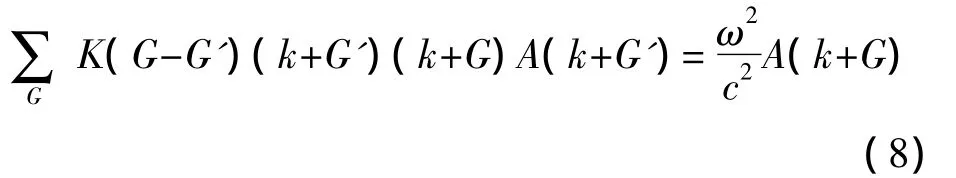
由式(8)可看出，對TE偏振的電磁波在光子晶體中的傳播問題就變成了求解對稱矩陣的本征值和本征函數的問題。

同理可得E偏振的方程如下:

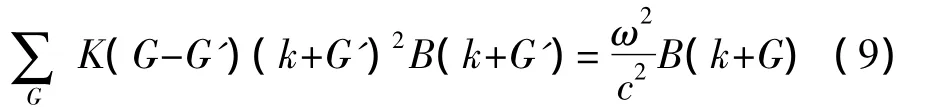
式(8)和式(9)分別是對無限多個倒格矢的求和。文中采用N個倒格矢的和來近似代替。因此這兩個方程分別變成含有2N×2N個矩陣元的本征值方程，可以采用數值計算的方法來求解。

考慮到每個原胞都分別由介質為εa和εb的兩種材料組成，因此上兩式中的系數可表示為:

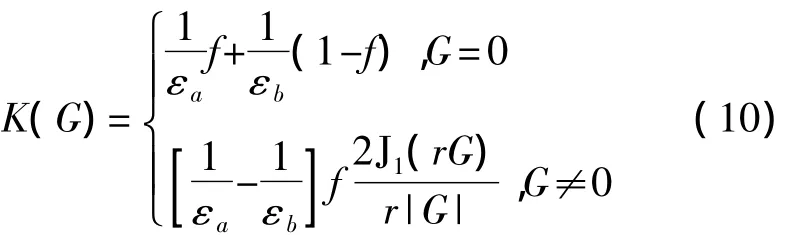
其中J1為一階貝塞爾函數;f為填充因子，表明介質柱或空氣柱占整個晶胞的百分比，對于正方晶格，f的表達式為:

將式(10)代入式(9)和式(8)，即可求出H偏振和E偏振的本征頻率。

2 數值計算結果與分析

計算采用的模型如圖1所示，介質柱的相對介電常數為εa，背景的相對介電常數為εb。計算時，采用441個平面波進行展開。

2.1 介質柱半徑對光子帶隙的影響

選用的晶格常數為a=0.1 mm，介質的相對介電常數為εa=11.6，背景的相對介電常數為εb=1，在固定介電常數和晶格常數不變的情況下，改變介質柱的半徑，使其半徑從0.2a變化到0.4a，通過大量仿真數據，分析TM模式和TE模式下光子晶體的帶隙變化規律。圖2(a)、2(b)以及2(c)分別為r=0.2a，r=0.3a，以及r=0.35a時，光子晶體TM模式下的帶隙分布圖。圖3(a)、3(b)以及 3(c)分別為r=0.2a，r=0.3a以及r=0.35a時光子晶體TE模式下的帶隙分布圖。

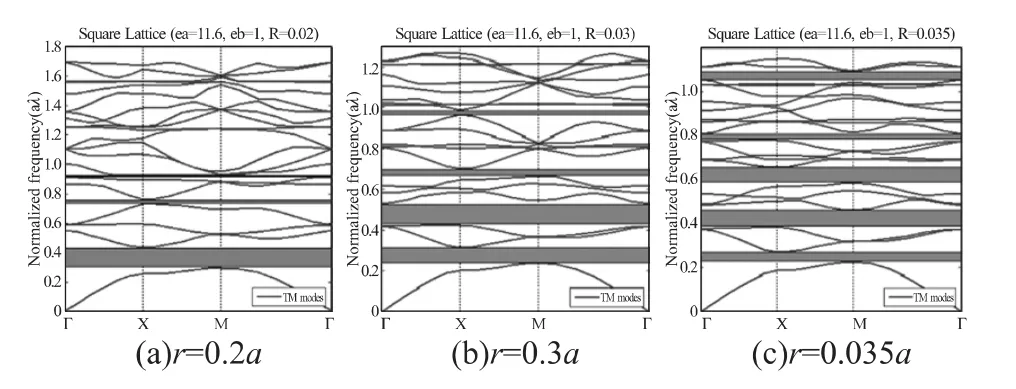
圖2 TM模式下正方晶格光子晶體帶隙分布圖(εa=11.6保持不變)

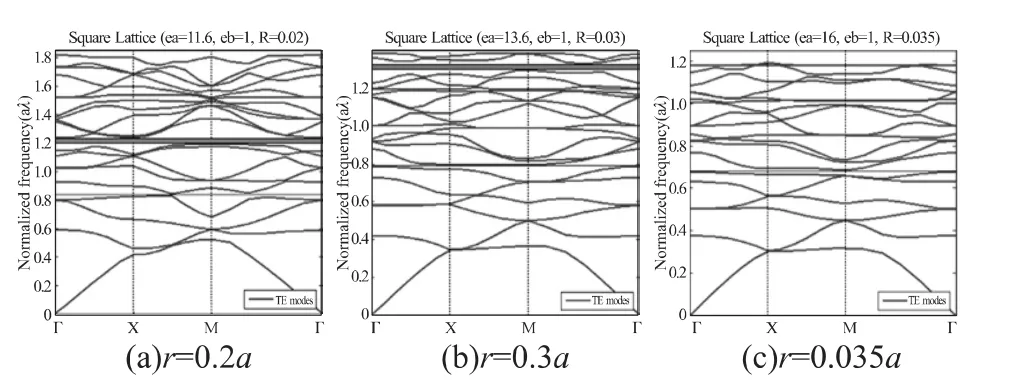
圖3 TE模式下正方晶格光子晶體帶隙分布(εa=11.6保持不變)

從表1中給出的數據可以看出，在TM模式下，當保持介質柱相對介電常數不變時，隨著介質柱半徑的增大，第1帶隙的帶寬慢慢變小;隨介質柱半徑的增大，帶隙的數量增多，出現第2、第3等多個帶隙，且第2帶隙的寬度將慢慢超過第1帶隙;隨介質柱半徑的增大，所有帶隙都往頻率低端移動。

表1 TM模式下不同介質柱半徑的光子晶體的帶隙分布THz

從表2中給出的數據可以看出，在TE模式下，當保持介質柱相對介電常數不變時，隨著介質柱半徑的增大，第1帶隙的帶寬慢慢變小;隨介質柱半徑的增大，帶隙的數量慢慢減少;隨介質柱半徑的增大，第1帶隙往頻率低端移動。

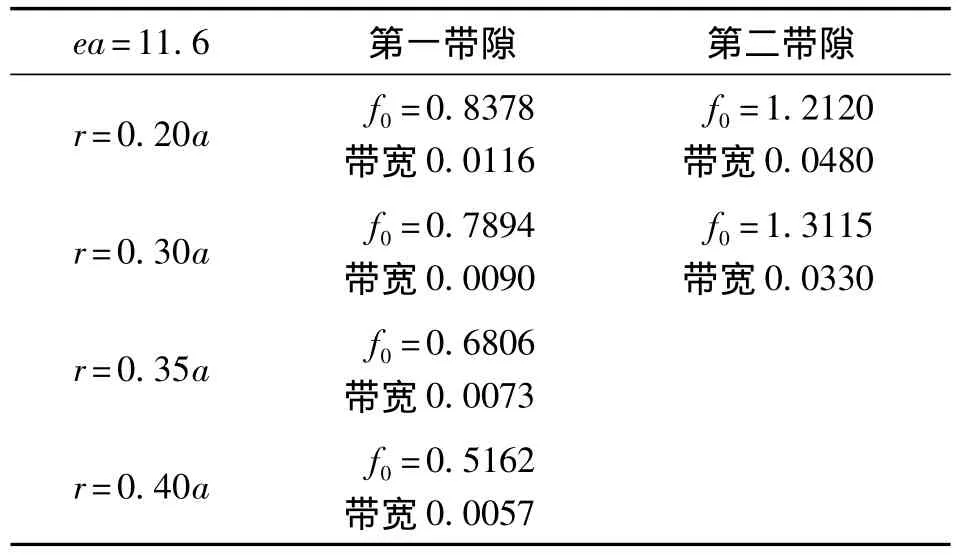
表2 TE模式下不同介質柱半徑的光子晶體的帶隙分布THz

比較TM模式和TE模式可以發現，TM模式比較容易出現帶隙，出現帶隙的數量差別比較大;在TM模式情況下，帶隙數量隨著介質柱半徑的增大而增多，而TE模式情況下，帶隙數量隨著介質柱半徑的增大而減少;在TM模式下，帶隙的帶寬較寬，比較容易實現帶內濾波的功能。

2.2 介電常數對光子帶隙的影響

選用的晶格常數為a=0.1 mm，介質柱的半徑r=0.2a，介質的相對介電常數為分別選取了εa=11.6，εa=13.6，εa=16和εa=20共四組數據，固定晶格常數和介質柱半徑不變的情況下，改變介質柱的相對介電常數，使其值從εa=11.6變化到εa=20，通過大量仿真數據，分析TM模式和TE模式下光子晶體的帶隙變化規律。圖4(a)、4(b)和4(c)分別為 εa=11.6，εa=13.6和εa=16時光子晶體TM模式下的帶隙分布圖。圖5(a)、5(b)和5(c)分別為εa=11.6，εa=13.6和εa=16時光子晶體TE模式下的帶隙分布圖。

圖4 TM模式下正方晶格光子晶體帶隙分布圖(r=0.2a保持不變)

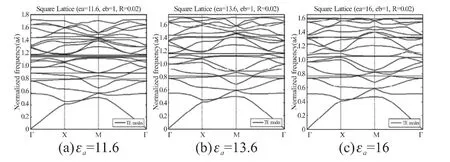
圖5 TE模式下正方晶格光子晶體帶隙分布圖(r=0.2a保持不變)

從表3中給出的數據可以看出，在TM模式下，當介質柱的半徑保持不變時，隨著介質柱相對介電常數的增大，第1帶隙的帶寬慢慢增大;隨介質柱相對介電常數的增大，帶隙的數量增多，出現第2、第3多個帶隙，但第1帶隙的寬度仍是最大的;隨介質柱相對介電常數的增大，所有帶隙都往頻率低端移動。

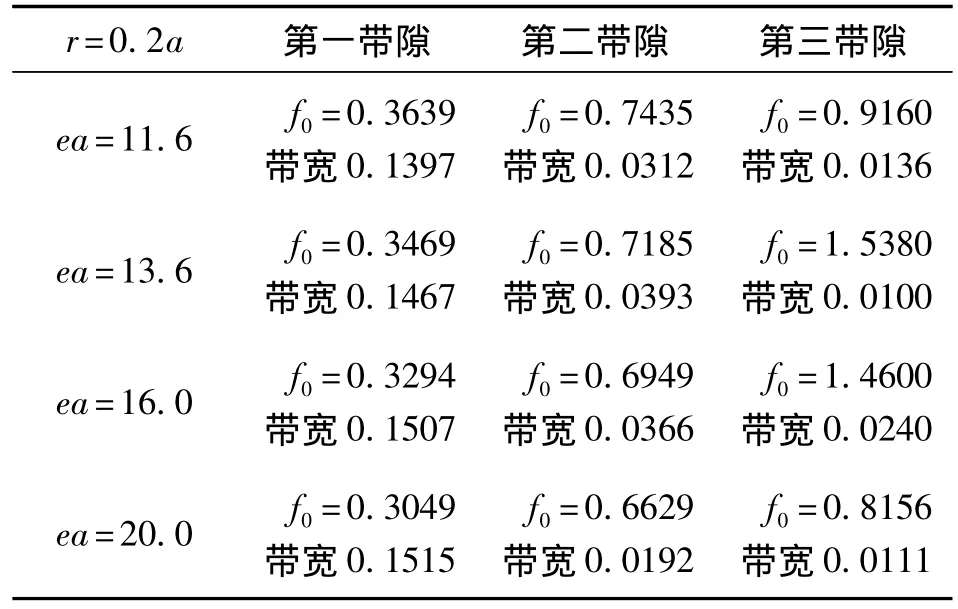
表3 TM模式下不同介質柱相對介電常數的光子晶體的帶隙分布 THz

從表4中給出的數據可以看出，在TE模式下，當介質柱的半徑保持不變時，隨著介質柱相對介電常數的增大，帶隙的數量慢慢減少;隨介質柱相對介電常數的增大，所有帶隙都往頻率低端移動;隨介質柱相對介電常數的增大，最大帶隙的帶寬慢慢減小;中心頻率最高的帶隙為主要帶隙，帶寬最大。

表4 TE模式下不同介質柱相對介電常數的光子晶體的帶隙分布 THz

比較TM模式和TE模式可以發現，TM模式比較容易出現帶隙;在TM模式情況下，帶隙數量幾乎不變，而TE模式情況下，帶隙數量隨著介質柱半徑的增大而減少;在TM模式下，帶隙的帶寬較寬，比較容易實現帶內濾波的功能。

3 結論

本文研究了THz波段的二維正方晶格光子晶體，理論研究發現，在特定的晶格常數下，改變介質柱的參數如介質柱的半徑大小或者介質柱的相對介電常數，都會引起光子帶隙的帶寬、中心頻率以及帶隙數量的相應改變，且呈現一定的規律性。這一結論對制作特定波段的光子晶體濾波器、波導等器件，具有實際應用價值。

［1］Fleming J W.High-Resolution Submillimeter-Wave Fourier-Transform Spectrometry of Gases［J］.IEEE Transactions on Microwave Theory and Techniques，1974，22(12):1023-1025.

［2］許景周，張希成.太赫茲科學技術和應用［M］.北京:北京大學出版社，2007.

［3］王少宏，許景周，汪力，等.THz技術的應用及展望［J］.物理，2001，30(10):612-615.

［4］張存林，張巖，趙國忠，等.太赫茲感測與成像［M］.北京:國防工業出版社，2008.

［5］姚建銓，路洋，張百剛，等.THz輻射的研究和應用進展［J］.光電子·激光，2005，16(4):503-510.

［6］John S.Strong Localization of Photonic in Certain Disordered Dielectric Superlattices［J］.Phys.Rev.Lett.，1987，58(23):2486.

［7］Yablonovitch E.Inhibited Spontaneous Emission in Solid-State Physics and Electronics［J］.Phys.Rev.Lett.，1987，58(20):2059-2062.

［8］Plihal M，Maradudin A A.PhotonicBand StructureofTwo-Dimensional Systems:The triangular latticce［J］.Phys.Rev.B，1991，44(16):8568-8571.

［9］Ho K M，Chan C T，Soukoulis C M.Existence of a Photonic Gap in Periodic Dielectric Structures［J］.Phys.Rev.Lett，1990，65(25):3152-3155.

［10］Gassagne D，Jouanin C，Bertho D.Hexagonal Photonic-Band-Gap Structures［J］.Phys.Rev.B，1996，53(11):7134-7142.

［11］Kazuaki Sakoda.Optical Transmittance of a Two-Dimensional Triangular Photonic Lattice［J］.Phys.Rev.B，1995，51(7):4672-4675.