論布魯爾SMK思想及其對當代數學教育的意義

　　布魯爾的SMK（sociology of Mathematic Knowledge）思想是其SSK（sociology of scientific knowledge）思想的重要組成部分，其內涵在于指出并不存在獨立于環境的所謂理性范式，即便數學知識具有很強的理論性和邏輯自恰性，也應該對它進行社會學分析；社會力量對于最深奧、最抽象的數學領域也能夠施加有力的影響，數學的威力就在于其中不可剔除的社會性成分。他以2+2=4為例，對其進行了具體的社會學分析；在這之前，他首先予以明確。
　　一、對2＋2＝4進行社會學分析具有可能性
　　“2+2=4這些術語的意義清澈如晶體，毫無彈性，以致命題只有單一的解釋，其真實性絲毫不容反駁，千秋萬世，顯示著理性所固有的洞燭真偽的能力”[1]，事實果然如此？
　　對此，知識社會學創始人卡爾·曼海姆（Karl Mannheim）明確指出，自然科學中質的方面所包含的因素或多或少與認知主體的世界觀交織在一起，但是“它的可定量領域，在很大程度上可以超脫于研究者的歷史——社會視角。”比如數學的歷史發展“在很大程度上決定于內在的因素。”因為數學知識有特殊的認識論地位，它與研究者的歷史社會觀在很大程度上是脫離的，對它的研究不受研究者觀念形態的影響，它是可以逃避思想批判的知識形式，無法對其進行社會學的分析，因而需要從知識社會學的研究視野中將其剔除。
　　布魯爾否定曼海姆的這種觀點，他認為數學知識并不具備社會學分析的豁免權，因為我們無法在物理、化學等經驗性知識和通常認為的包括數學、邏輯學在內的非經驗性知識之間做出區分，更不能將不同的心智器官視為不同知識的產生源泉，比如說感覺經驗器官產生關于經驗事實的有條件的知識，而理性的器官則產生關于邏輯和數學必然性的真理。
　　布魯爾以因果性、公平性、對稱性等原則構成的綱領為理論平臺，指出并不存在超文化的所謂的理性范式，對于數學知識也應該進行社會學分析，從而將因果性指導原則推及到了傳統上認為是自然科學知識中的硬核部分——數學領域，“我們至今所討論的問題以及問題討論的結論將從經驗知識領域和有條件的知識領域，擴展到‘必然性’真理的王國”。所以對包括2+2=4這樣的數學知識也是可以進行社會學的分析的。
　　另外，為了批判2+2=4具有意義確定性的觀點，布魯爾還理性地構建了語境。他認為2+2=4這個式子的含義并非如理性主義者所想的那樣確切，它依賴于具體的語境，比如在他所構造的僅有0、1、2、3、4這樣5個數字的有限算數（finite arithmetic）的環境中，當人們回答3+3=1，3+4=2，2*2=4，3*3=4的時候，2+2=4的意義就異于它在十進制中的意義。也即單單拿出一個孤立的式子2+2=4，實際上我們無法理解其確切、具體的含義，我們無法判斷它究竟是應用于十進制還是五進制的語境中。我們不能因為五進制的應用范圍小于十進制的，就認為五進制的應用不合理、沒有意義。這也是布魯爾強綱領中公正性原則的貫徹，即“它應當對真理和謬誤、合理性或者不合理性、成功或者失敗，保持客觀公正的態度。這些二分狀態的兩個方面都要加以說明。”
　　二、對2＋2＝4“非社會學分析”觀點的批判
　　布魯爾采用他一貫主張的自然主義、經驗主義的原則，對2+2=4的產生和建立進行了分析。他通過對2+2=4低階（low-status）、中階（middle-status）和高階（high-status）三階證明的批判，得出“2+2=4的可信性并不是建立在證明的基礎之上，具有充分必要條件的證明并不存在”的結論，針鋒相對地反駁了勞丹的觀點——由證明產生的理性的信念是2＋2=4的可信性的根源。
　　首先，布魯爾對2+2=4的低階證明進行了批判。低階證明是普通人對這個公式的認識過程。這時人們往往借助實物進行證明，從一堆蘋果中選取一對兒，數數：一、二。從這堆蘋果中另取一對兒，數數：一、二。然后將兩對并行放置，數數：一、二、三、四。這就是2＋2=4的原因。最后的結論可能是：所有與之相似的群體都會產生與之同樣的結果。于是：2+2=4。但布魯爾認為，僅僅因為這些蘋果現在以這種方式作為，并不能說明它們將會總是以同樣的方式作為。如此方式建立的一個歸納和經驗的真理，顯然無法推延到建立2+2總是并且必須等于4這樣一個永恒真理。所以，以這種方式對2+2=4進行的低階證明，是不能成立的。
　　其次，布魯爾對2+2=4的中階證明進行了批判。弗雷格（Frege）和皮諾（Peano）所使用的證明用相繼關系定義自然數，1是0的后繼者，2是1的后繼者，2也是0的后繼者的后繼者，等等。符號表示為：1=S（0），2=S（1），或者2=S（S（0））。這樣，2+2=S（S（0））+S（S（0）），4=S（S（S（S（0））））。顯然，要使用這種方法證明2+2=4，我們就要追尋S的使用次數。事實上也就是在數數，這樣，在證明之初就已經預設了要證明的結果。
　　再次，布魯爾對2+2=4的高階證明進行了批判。職業邏輯學家麥克爾（J.L.Mackie）在1966年對于2+2=4做了一個12步的高階證明，第1步是他用符號化的語言表達了進行低階證明的記數者（quantifiers）的行為。后2步是對第1步信息的重復，但消解掉了記數者存在的信息。以后的幾步都是對前面步驟的歸約，到了第11步，他把一開始消解掉的記數者又拾了回來。第12步則表達了這樣的信息，即對于K、L和M集合，如果K只有2個元素，L也只有2個元素，那么當M把兩個集合合并，M就是一個四元素的集合。麥克爾的結論是，基于符號邏輯的12個步驟進行演算的這個高階證明，與我們進行低階證明時所依賴的完全是一樣的思維過程，即我們依賴于2+2=4這個例證。
　　在布魯爾看來，這個所謂的高階證明不外乎是引進了a、b、c、d四個符號，a和b形成一個2元素的集合K，c和d形成一個2元素集合L，a、b、c、d則形成了一個4元素的集合M，其實，它們與低階證明并無二致，至多前者是一個身體性的收集活動，后者是一個符號性的操作活動。顯然麥克爾的證明恰恰說明2+2=4奠基于原始的社會性活動中。布魯爾對此深刻地指出，如果說我們從建構中得到了什么，原因還是在于我們作為孩童時刻接受的訓練。對于2+2=4來說，我們接受它，是因為它來自傳統，來自社會性活動，而不是所謂的證明或自明。
　　這樣，對于2+2=4來說，無論是低階證明、中階證明還是高階證明，都是建立在社會性活動的基礎上的，都可以在其中發現社會因素的存在。
　　三、布魯爾對2＋2＝4的社會學分析及其對當代數學教育的意義
　　布魯爾認為，2+2=4之所以具有可信性，不在于它得到了證明，而在于它是一種約定，并對這種約定的社會本性進行了如下分析：
　　布魯爾首先將數學與語言、學習數數與學習拼寫進行了類比，“我們在數數中受訓，正如我們在字母中受訓一樣，我們學習加法就像我們學習拼寫一樣”，繼而指出無論是學習數學還是學習語言，它們都涉及規則的遵守，“但是沒有人不把字母或拼寫規則視作社會約定”，“當孩子們在學習算術時，孩子們所受的訓練受制于他們的老師，還有什么比在學習數數過程中堅決要求孩子必須說4之后是5，3之后是4更強烈的權威訴求嗎”？而整個“傳授過程必須被看作是社會性決定的和有社會性條件的”。“數學的必然性不過是通常附著于某種更重要的社會約定的道德必然性的一個種類，數學的嚴格性不過是一種社會需要的嚴格性，即這種社會需要我們使用這種技藝而不是那種技藝”。
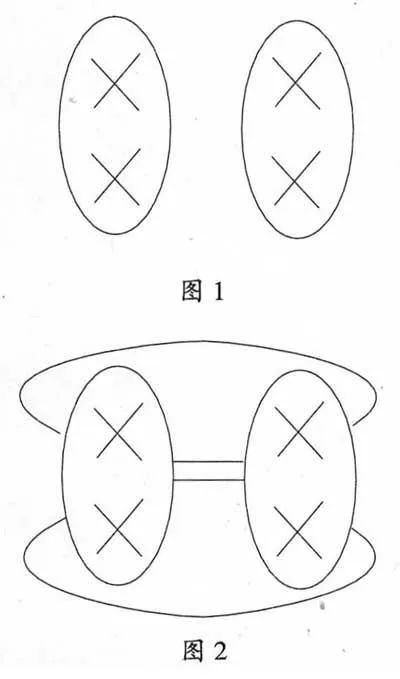
　　對于2＋2＝4的使用，已經日常化到了我們的實踐當中。而對于2＋2＝4的這種約定，不外乎說明了一種我們集體所認可的方式，這從維特根斯坦的著作中可以清晰發現，“要明白2＋2＝4，你只需看一下圖1”
　　這樣的分類模式一定是已經訓練好了的，否則為什么不是圖2所示？
　　不同的分類模式正是有限論（一個詞語的現今用法無法決定其將來的用法）得以建立的基礎，因為人們的社會約定不同，導致分類模式相異，進而也將直接導致體現在數學認知上的差異：2+2=4？2+2=5？布魯爾認為，事實上2+2=5一點都不離經叛道，它也不是我們大腦正常工作的劇烈破壞或者是徹底的洗腦，因為如果更換一個情境，比如拉卡托斯在《證明和反駁》一書中所設置的虛擬情景——設想一下我們要郵遞兩個各自重量為2磅的物品，它們被裝在一個重量為1磅的盒子里遞，那么在這個包裹中兩個2磅就是5磅！我們樸素地認為2+2=4，是因為有著這樣一個輔助的約定，即包裝材料的重量為零。
　　2+2=4而不是2+2=5，這并不說明前者對應著某種神秘的數學現實，人們之所以偏愛拉卡托斯的“無重量”加法，是因為“對加法建立一個約定意味著解決一個協調問題，就是說要使每一個人適應于同一個程序”，完全是出于實用的理由。2+2=4這個經由諸多證明得出的穩定結論的意義，就在于它“具有的制度性的特征”。
　　拉卡托斯就曾經指出，說數學的某些方面、論證的某些風格呈現出永恒真理的外觀，那是因為此時的數學處于常規發展時期，它的范式沒有受到批判。布魯爾也認為數學中不存在任何終極性的邏輯本質，數學與物理學、化學等其他科學一樣，都可以利用猜想、反駁的方法加以研究。說數學是一目了然的，那是因為它處于一個沒有受到批判的研究范式下，而來源于庫恩的范式，當然為社會性因素的進入提供了方便之門！
　　可以說，教育、科技一直以來尤其現在更是我國的大事，教育觀必須以科技觀為先導，更具體地講，數學教育觀要以數學觀為先導。而數學觀作為一種理論概括，它應該與數學史的發展保持一致，邏輯的總要與歷史相統一。而當前在我國數學教育中，理性推導與公式記憶的教學法一直占據主流，數學史的教學非常薄弱，而數學史以及其中形成的數學觀對于數學教育的重要意義已經顯而易見：改變數學枯燥、抽象的形象；加大數學文化功能的研究；提升學生人文素質的重要途徑；讓學生不僅知道數學之然而且知其所以然，從而為進一步創新打下堅實基礎。
　　參考文獻
　　[1] [英]伊姆雷·拉卡托斯.證明與反駁.上海：上海譯文出版社，1987.
　　[2] [德]卡爾·曼海姆.意識形態與烏托邦.北京：商務印書館，2002.
　　[3] [美]拉里·勞丹.進步及其問題.北京：華夏出版社，1990.
　　[4] [英]巴里·巴恩斯等.科學知識——一種社會學的分析. 邢冬梅等譯.南京：南京大學出版社，2004.
　　[5] [英]大衛·布魯爾.知識和社會意象. 艾彥譯.北京：東方出版社，2002.
　　[6] 涂紀亮主編.維特根斯坦全集（7）. 徐友漁，涂紀亮譯.石家莊：河北教育出版社，2003.
　　[7] 楊渭清.HPM視野下的數學教育.西安文理學院學報：自然科學版，2010（7）.
　　（責任編輯 劉永