補償法研究拋體運動

許建明

(浙江師范大學(xué)數(shù)理信息學(xué)院 浙江 金華 321004)

1 運用補償法計算拋體運動軌跡

如圖1所示，傳統(tǒng)方法求解一般拋體運動軌跡時主要是將阻力直接分解到兩個互相垂直的方向，然后利用牛頓第二定律積分.但對于空氣阻力與速度不是線性關(guān)系時，積分較繁瑣.運用補償法，可以大大簡化積分運算.

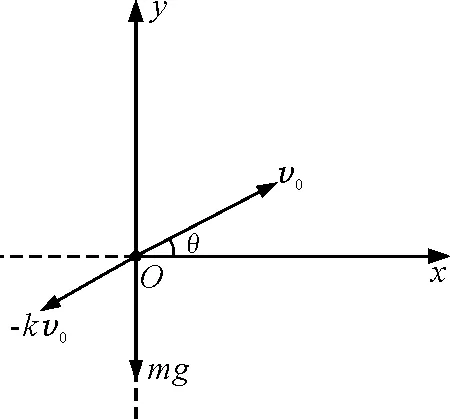
圖1 傳統(tǒng)求解圖

圖2 補償法求解圖示

如圖2所示，處于原點O,質(zhì)量為m的質(zhì)點初速度為v0與x軸正向的夾角為θ，空氣阻力f=-kv0,與速度方向相反.如果在豎直方向同時補上大小相等，方向相反的速度v′不會影響物體的運動，且滿足

kv′=mg

(1)

(1)考慮向下的速度-v′會使物體受到一向上的空氣阻力kv′，由于kv′=mg,因此，物體向下做勻速直線運動，位移為

(2)

(2)將向上的速度v′與初速度v0矢量合成為v，與x軸正向的夾角為α，空氣阻力變?yōu)?kv與x軸負向的夾角為α，將v和阻力分解到坐標軸，列出相應(yīng)的運動學(xué)方程

vx0=vcosα=v0cosθ

(3)

vy0=vsinα=v0sinθ+v′

(4)

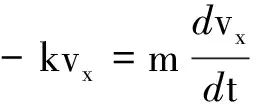
(5)

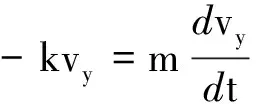
(6)

對式(5)積分

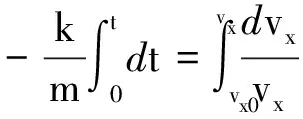
可得

(7)

(8)

同理,可得此種情況下y方向的位移

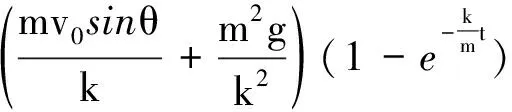
(9)

將兩種情況疊加可得物體運動的參數(shù)方程為

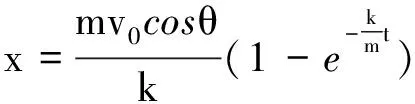
(10)

y=y1+y2=

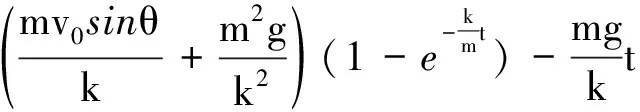
(11)

物體在空氣中受到的阻力與物體本身的形狀、空氣密度、特別是和物體的速率有關(guān)，大體來說,物體速率低于200 m/s可認為阻力f∝v2[1].文中討論的阻力為f=-kv，對于更高次的f=-kvβ(β>1)一般采用內(nèi)稟方程解物體運動微分方程的方法求解[2]，在此不再贅述.

根據(jù)此方法的方程為

mg=kv′β

(12)

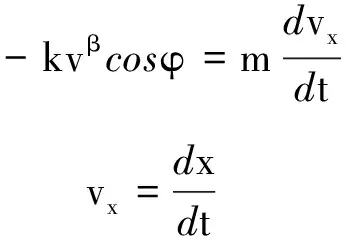
(13)

(14)

圖3是空氣阻力與速度的一次方成正比時，不同速度物體運動軌跡的大致形狀.由圖3可知，在一定的速度范圍內(nèi)，速率越大拋體飛得更高更遠，且有空氣阻力時其軌跡不是拋物線，過最高點后更陡.

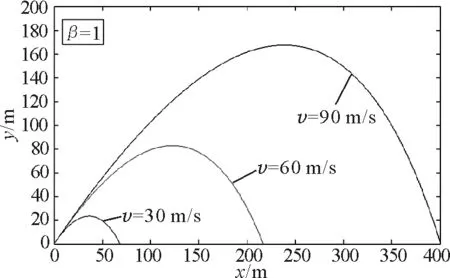
圖3 β=1時不同初速度軌跡

2 利用MATLAB求解最佳拋射角

根據(jù)式(10)和式(11)并利用MATLAB求解初速度一定時的最佳拋射角.以我國優(yōu)秀運動員在鉛球比賽中的投擲情況作為初值條件，在2006年全國田徑大獎賽肇慶站男子鉛球比賽中，推出最好成績 17.02 m時，鉛球的出手速度v0=12.40 m/s，出手角度為40.6°,出手高度為h0=2.47 m[3]，且鉛球的標準質(zhì)量為7.257 kg，球體阻力系數(shù)k約為0.5[4].

將拋射角θ(0°≤θ≤90°)等分為10份[5]，畫出相應(yīng)的軌跡曲線如圖4所示.

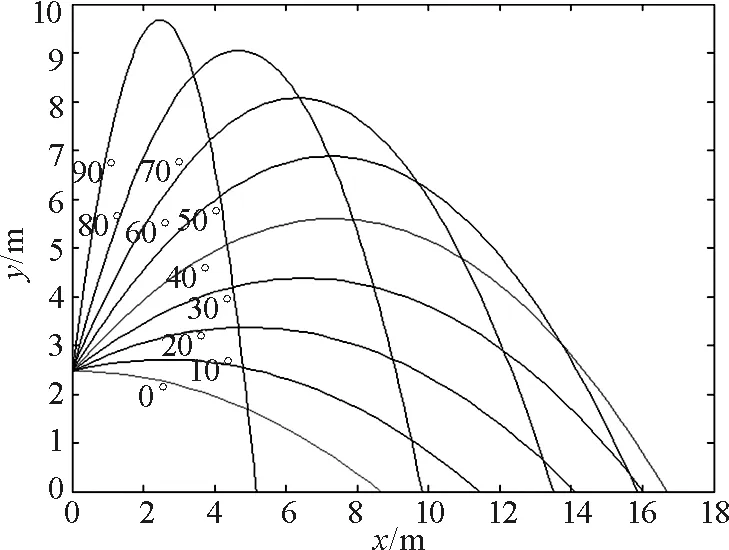
圖4 不同拋射角軌跡圖

由圖4可知,隨著拋射角的增大拋程也增大，但超過40°后,拋程隨拋射角增大而減小，因此，最佳拋射角應(yīng)該在30°～50°之間.下一步是每隔一定的步長d計算其拋高(鉛球最高位置y)和拋程(鉛球最遠處x).

在圖5中，曲線Ⅰ表示每隔d=1°時計算拋程.由圖可知從30°～45°之間都是光滑的，但45°～46°卻有很大的下降，并且之后下降速率不變.這是由于超過45°后阻力在豎直方向的分量比水平方向的要大，豎直方向起著主導(dǎo)作用.

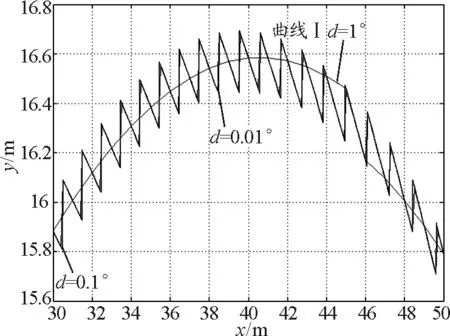
圖5 拋程隨角度變化關(guān)系圖

另外兩條折線好像已經(jīng)重合，分別是每隔0.1°和0.01°計算拋程.發(fā)現(xiàn)兩條線基本上是以d=1°的曲線為中心振動上升，整體趨勢與曲線Ⅰ相同，都是過45°后抖動更為劇烈.

不同拋角對應(yīng)的拋程和拋高如表1所示.

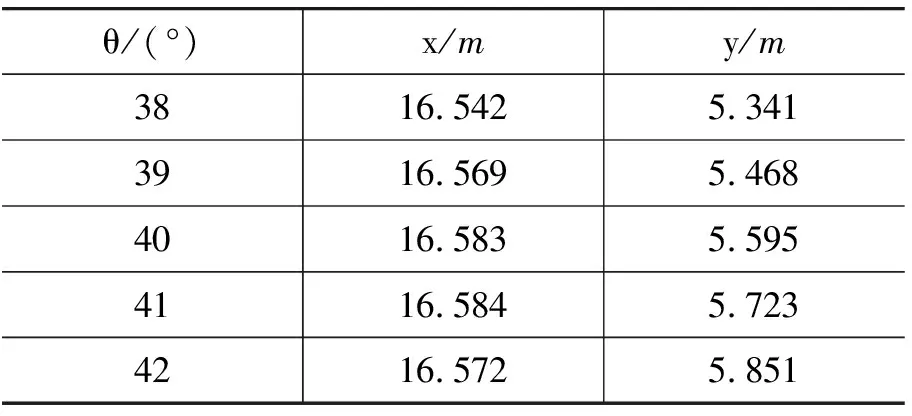
表1 不同拋射角對應(yīng)的拋程和拋高

由表1可知當拋射角為41°時拋程最大為16.58 m，這與實際拋角40.6°的拋程17.02 m相差很小.

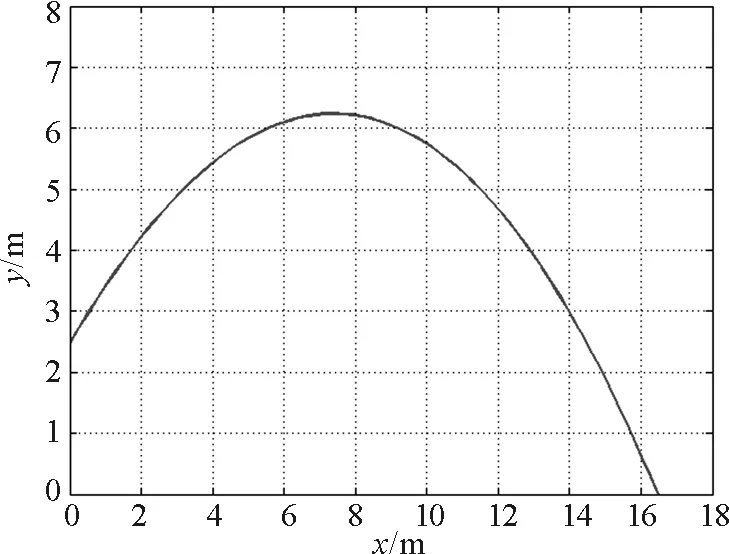
圖6 最佳拋射角運動軌跡

最后,模擬出鉛球以最佳拋射角出手時的運動軌跡，如圖6所示.

3 總結(jié)

本文用補償法給出了有空氣阻力時,拋體運動軌跡的參數(shù)方程，這種方法還可以運用到解決帶電粒子在電磁場中運動的問題，也為中學(xué)解答這類物理問題提供了另外一條思路.最后利用MATLAB直觀、精確、快速地解決了最佳拋角問題，為解決類似問題提供了新的途徑.

參考文獻

1 漆安慎，杜嬋英.力學(xué).北京：高等教育出版社，2010.41

2 周衍柏.理論力學(xué).北京：高等教育出版社，2009.24～25

3 王倩,等.對兩名不同水平男子鉛球選手投擲技術(shù)的生物力學(xué)分析. 北京體育大學(xué)學(xué)報，2007, 30(3)：404

4 郝成紅.考慮拋體空氣阻力的拋體射程.大學(xué)物理，2008,27(12)：21～22

5 尤明慶.關(guān)于鉛球最佳出手角的討論.力學(xué)與實踐，2013,35(1)：68