火車汽笛聲的頻率變化曲線的定量分析

卞清

(解放軍理工大學理學院 南京 江蘇 211101)

1842年奧地利物理學家多普勒在鐵路邊散步時,一列火車鳴著汽笛駛過，他注意到列車駛過時,汽笛聲的音調(diào)發(fā)生了變化，這引起了他的興趣，經(jīng)過研究發(fā)現(xiàn)，當波源和觀察者相對運動時，觀察者所接收到的頻率和波源的頻率不等，這就是多普勒效應(Doppler effect)．

電磁波也存在多普勒效應．電磁波以光速傳播，電磁波的多普勒效應公式要利用狹義相對論推導．聲波和電磁波的多普勒效應原理在科學研究和工程技術(shù)中都有著廣泛的應用．

1 駛過靜止觀察者身旁的火車汽笛聲頻率與火車位置的關(guān)系

設(shè)波源的振動頻率為ν,觀察者接收的振動頻率為ν′，觀察者相對介質(zhì)靜止，波源以速度v運動．如果波源沿著與觀察者的連線運動, 觀察者所接收到的頻率與波源的頻率之比為

(1)

式中“-”是波源向著觀察者運動，ν′>ν頻率升高；“+”是波源遠離觀察者運動，ν′<ν頻率下降．

當波源的運動方向與二者的連線不平行時，如圖1，只要將式(1)中的波源運動速率v換為vcosθ，θ是波源運動方向與二者連線的夾角[1]

(2)

即然波源運動而觀察者靜止，那么波源與觀察者的相對位置就是變化的，θ角就會隨著波源的位置而改變．如圖1中，波源S是火車的汽笛，設(shè)火車相對介質(zhì)沿著x軸做勻速直線運動，汽笛t時刻的坐標

x=x(t)．觀察者靜止于P處(xp=0)，與火車軌道的垂直距離為d．考慮到聲波傳播所用的時間，觀察者在t時刻接收到的汽笛發(fā)出的聲波是t時刻之前的(t-Δt)時刻，汽笛位于x(t-Δt)位置所發(fā)出的.

圖1 波源和觀察者的相對位置

注意到圖中的火車坐標x(t)<0，由直角三角形SOP的邊長關(guān)系可得

(uΔt)2=(x-vΔt)2+d2

(3)

夾角θ滿足

(4)

式(2)、(3)、(4)聯(lián)立，可解出

(5)

式(5)即為經(jīng)過靜止觀察者旁邊的火車位置與汽笛聲頻率的關(guān)系式,其中聲波速率u=340 m/s，火車速率為v，d是觀察者離火車軌道的距離．

2 計算結(jié)果與分析

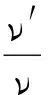
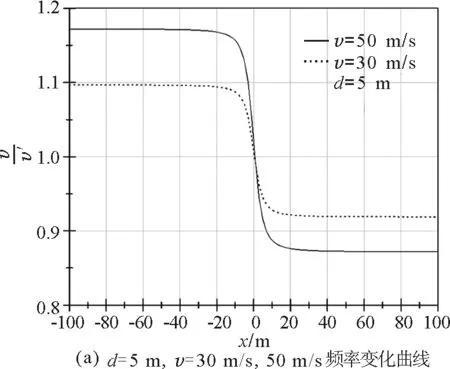
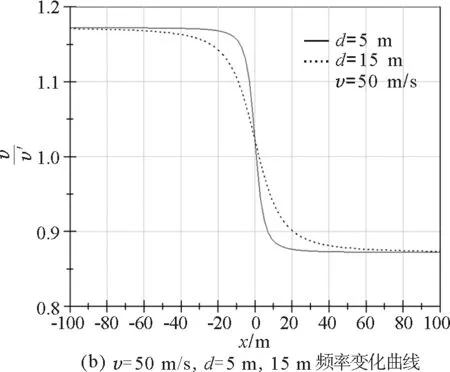
圖2

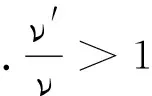
(1)圖2(a)中兩條曲線分別是火車速率為50 m/s和30 m/s，觀察者與軌道的距離為5 m.

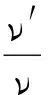
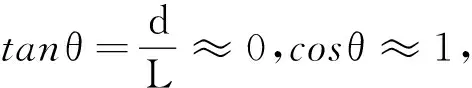
火車以30 m/s的速率運動時

在這兩種速率下，頻率最大相對改變量分別為

(2)圖2(b)中的兩條曲線分別是觀察者與軌道的距離為5 m和15 m，火車速率為50 m/s

從圖中可以看出,汽笛聲的最高和最低頻率相同．頻率從最高到最低的連續(xù)變化過程發(fā)生在|x|

3 結(jié)論

駛過靜止觀察者身邊的火車汽笛聲的音調(diào)由最高到最低，經(jīng)過觀察者附近時有一段連續(xù)的降調(diào)過程．觀察者離火車軌道越近，變調(diào)越快．

本文只分析了靜止觀察者接收到的火車汽笛聲的音調(diào)變化，對運動的觀察者,如在汽車中的觀察者所聽到火車汽笛聲的音調(diào)變化可以用相同的方法來定量分析．

參考文獻

1 吳王杰.大學物理學(下冊).北京：高等教育出版社，2009.45