大學熱學的解題方法剖析*

李根全 宋金璠 張萍 楊興強

(南陽師范學院物理與電子工程學院 河南 南陽 473061)

1 引言

卓越教師是指在教育理念、教學方法、科研能力等方面達到一定的高度，能成長為省內(nèi)外有重要影響力的教學名師，能夠從經(jīng)驗型教師向研究型教師轉(zhuǎn)型[1]．教師在教學過程中，要不斷結(jié)合實際，改變教學方法和教學手段，因為教師的工作不是只教給學生做作業(yè)，而是努力構(gòu)建學生的知識結(jié)構(gòu)，并用種種方法刺激學生的學習欲望．

在長期的教學過程中，我們結(jié)合物理學的學科特點，總結(jié)了建模法、求導(dǎo)法、積分法、圖解法、近似計算法、類比法、反證法等幾種常用的解題方法，通過使用不同的解題方法去研究物理學相關(guān)問題，加深學生對物理問題的理解，進而強化物理概念，提高思維能力，做到舉一反三，觸類旁通，這才是教育的關(guān)鍵問題．下面以熱學課程教學為例來說明之.

2 幾種常用的解題方法

2.1 建模法

建模法是物理學的基本研究方法之一．由于物理問題一般是復(fù)雜的，因此處理問題時，常突出主要矛盾，暫時略去一些次要因素，把實際問題抽象成一個理想模型，如理想氣體、準靜態(tài)過程、可逆循環(huán)過程等都是理想化模型．在遇到這類問題時，必須注意的是：該處忽略了哪些因素，如果考慮了這些因素，將得到怎樣的結(jié)果．

【例1】1 mol理想氣體的狀態(tài)方程為

這是在體積趨向于零的剛球模型

基礎(chǔ)上得出的，既沒有考慮分子的大小，也沒有考慮分子之間的相互作用[2]．

由于實際氣體分子總要占據(jù)一定的空間，考慮到分子的體積，理想氣體分子的勢能為

則對應(yīng)的方程為

在剛球模型的基礎(chǔ)上若考慮分子之間的吸引力，其勢能為

其中t是常數(shù)(通常t=6)，-Φ0是r=r0時的勢能，此時對應(yīng)的物態(tài)方程為范德瓦耳斯方程

如果將分子之間的引力和斥力都考慮在內(nèi)的話，其相互作用勢

其中的A，B，m，n取不同數(shù)值可表示不同相互作用勢，這與昂內(nèi)斯方程中的系數(shù)A和B等可取不同數(shù)值類同，可粗略認為所對應(yīng)的方程就是昂內(nèi)斯方程[2]．

通過這樣層層遞進地討論，使學生對氣體的各種狀態(tài)方程及使用范圍有了清晰的認識，形成了立體化的知識框架．

2.2 求導(dǎo)法

由于物理量的變化一般是非均勻的，因而需要結(jié)合數(shù)學原理用求導(dǎo)的方法來解決這類問題．在熱學中常常使用求導(dǎo)法計算極值問題，比如計算最概然速率、臨界點參量和任意熱力學過程溫度的最高點．

【例2】1 mol單原子理想氣體經(jīng)歷如圖1所示的a→b(為一直線)過程，試討論從a→b的過程中吸收和放出熱量的情況．

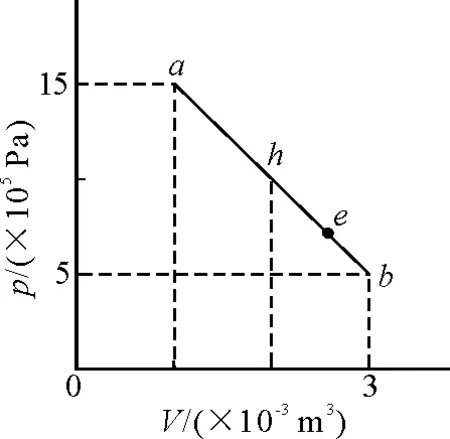
圖1

分析：根據(jù)理想氣體的狀態(tài)方程可以得出，從

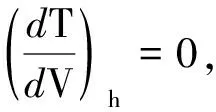
通過以上分析后再討論從a到b的過程中吸收和放出熱量的情況就簡單多了．

對該問題的討論，學生完全掌握了過程方程、吸熱放熱轉(zhuǎn)換、溫度變化及熱容量等概念，是具有代表性的習題，可以作為熱學教學的典型案例．

2.3 積分法

由于很多物理量是變化的或不均勻的，在計算時會用到積分法，比如氣體膨脹對外所做的功、系統(tǒng)從外界吸收的熱量、熵的變化、氣體在某一速率區(qū)間內(nèi)的分子數(shù)、求平均值等，所以，積分法在物理學中是一個很重要、很有用的數(shù)學工具．

【例3】從范德瓦耳斯方程導(dǎo)出熵的表達式

解：由范德瓦耳斯方程得

又

dQ=dU+pdV

聯(lián)立以上各式得

ΔS=S-S0=

即

利用此式不僅可以計算范德瓦耳斯氣體在任意狀態(tài)的熵[4，5]，還定量說明了“熵是態(tài)函數(shù)”的定義，為熵的討論提供了科學依據(jù)．

2.4 圖解法

物理量之間的函數(shù)關(guān)系，除了可用公式表示外，還常用圖示的方法來表示，它們比較直觀，易于分析問題，在熱學教學過程中常常使用圖解法進行討論[6]．

【例4】如圖2，ab表示一定質(zhì)量理想氣體所經(jīng)歷的準靜態(tài)過程，求ab過程中系統(tǒng)對外所做的功．

圖2

解：為了解決這一問題，過a和b分別作等溫線T及T-ΔT，并且過a作等體線V，由熱力學第一定律，系統(tǒng)在ab過程所吸收的熱量

所以

而

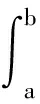
式中Aabdea為曲邊形abdea的面積，又

ΔUab=ΔUac

因而

ΔUac=ΔQac=-ΔQc a

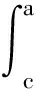
故

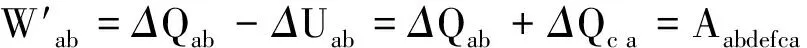
即系統(tǒng)在ab過程中對外所做的功等于多邊形abdefca的面積．

這樣利用圖形的面積將ab過程系統(tǒng)對外所做的功直觀地表示出來，同時還可以推廣到任意過程ab：若末態(tài)b位于過a的等體線V的右下方，則末態(tài)的體積比初態(tài)的體積大即系統(tǒng)經(jīng)歷一膨脹過程，對外做功．若末態(tài)b位于過a的等體線V的左上方，則系統(tǒng)經(jīng)歷一體積減小的過程，系統(tǒng)對外做負功，功的數(shù)值仍用T-S圖上一多邊形的面積來表示．類似的情形還有關(guān)于熱容量、熱機的效率、熵、熱量等的討論[6～8]．這種方法把抽象復(fù)雜的物理過程有針對性地表示成物理圖像，將物理量間的代數(shù)關(guān)系轉(zhuǎn)變?yōu)閹缀侮P(guān)系，運用圖像直觀、形象、簡明的特點，來分析解決物理問題，由此達到化難為易，化繁為簡的目的，有助于學生快速解題，進而提高學習效率，優(yōu)化課堂教學．

2.5 近似計算法

有些物理問題在計算過程中，函數(shù)關(guān)系比較復(fù)雜，處理比較困難，一般根據(jù)條件將函數(shù)關(guān)系采用不同形式的近似處理，從而使問題得以簡化．

【例5】求標準狀態(tài)下1.0 m3氮氣中速率在500 m/s到501 m/s之間的分子數(shù)．

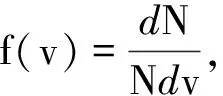
在標準狀態(tài)下1.0 m3氮氣的分子數(shù)即Loschmidt常量n=2.686 8×1025m-3，所以

要計算上式才能得到速率在500 m/s到501 m/s之間的分子數(shù)，直接計算比較復(fù)雜，在計算中將dv近似地取為Δv=1 m/s，可以認為它足夠小，在這速率區(qū)間內(nèi)的分子數(shù)為[9]

由于受實驗條件、數(shù)學手段等的限制，近似計算法是物理學中常常遇到的問題，掌握這種方法可以使復(fù)雜的問題簡單化，同時不影響討論結(jié)果．

2.6 類比法

類比法是把已知的關(guān)系式或求出的關(guān)系式與標準式比較，確定相關(guān)物理量及其性質(zhì)，這種方法是物理學中常用的方法，在熱學學習中也常用到．比如，熱學中常以理想氣體為例，討論其狀態(tài)方程、熱力學過程特點、功、熱量、內(nèi)能的變化關(guān)系并在p-V圖上予以表示，利用類比法，可以討論理想氣體在T-S圖上的性質(zhì)、特點及表述[10～12]．

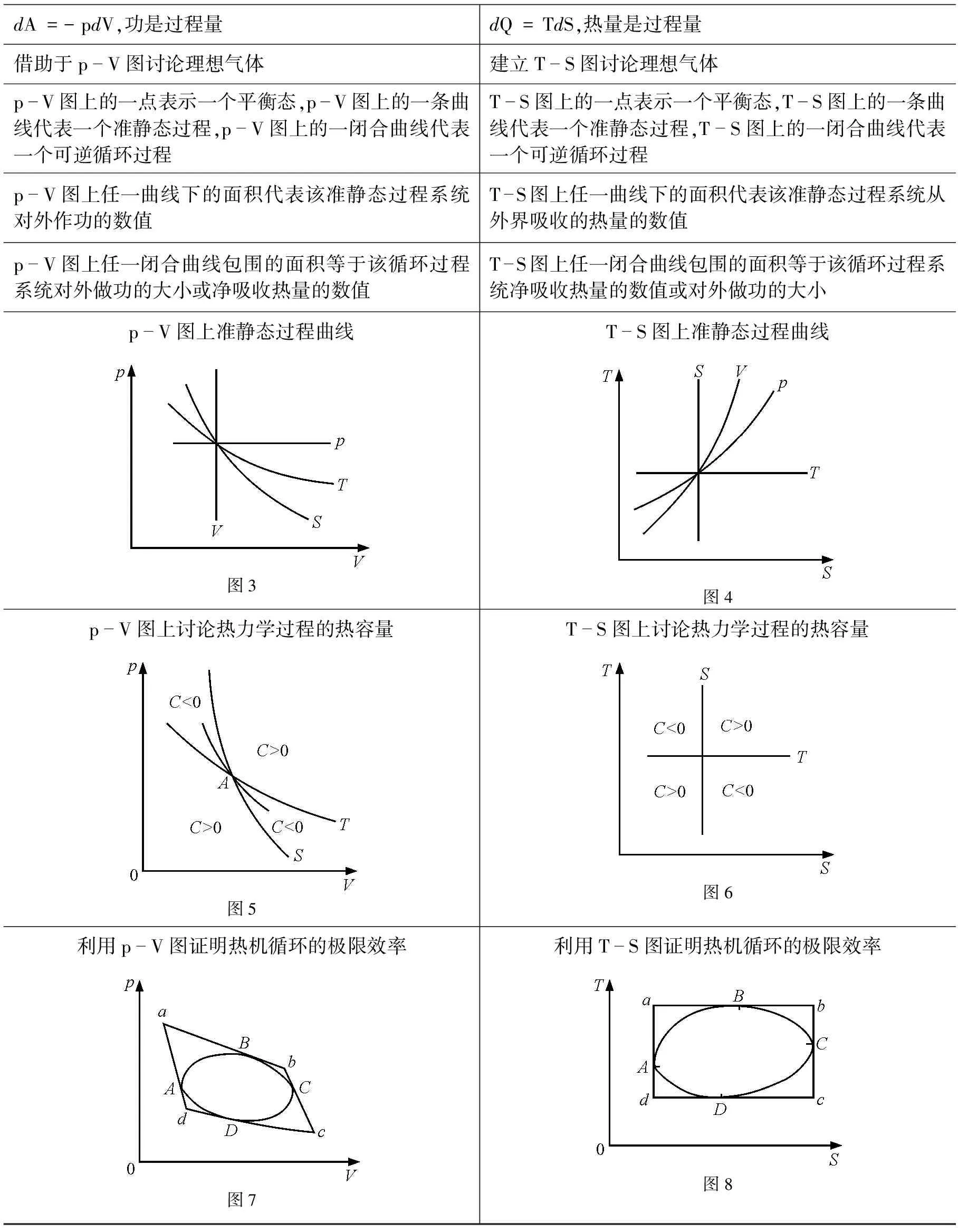
表1 p-V和T-S對應(yīng)關(guān)系比較

通過以上對比，使p-V圖和T-S圖的特點、性質(zhì)和應(yīng)用清晰明了．類比法是一種重要的思維方法，把抽象的知識形象化，把復(fù)雜的問題簡單化，使知識融會貫通，從而提高學生分析問題和解決問題的能力．在教學過程中有意識地使用類比法，使學生受到熏陶和訓(xùn)練，為終身學習奠定基礎(chǔ)．

2.7 反證法

反證法是物理學中常用的方法之一，對于無法直接證明的命題，只能采用反證法，比如,熱力學第二定律兩種表述的等效性、兩絕熱線不能相交、絕熱線與等溫線不能相交于兩點等，這些命題只能用反證法得出謬誤的結(jié)論．

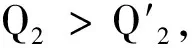
圖9

反證法不僅可以單獨使用，也可以與其他方法結(jié)合使用，并且可以在論證一道命題中多次使用，只要能正確熟練運用，就可以做到精巧、直接、巧解難題、說理清楚、論證嚴謹，提高解題能力．

3 結(jié)束語

“物理題目難做”是物理教、學過程中遇到的普遍問題，做習題主要是檢驗對基本概念和基本規(guī)律的理解情況，是將已學理論用于分析問題和解決問題的過程，只有掌握了正確的解題方法，才能做到理論、實踐的有機結(jié)合，收到事半功倍的效果．解題的過程也是利用所掌握的知識進行分析、判斷和邏輯思維的過程．做習題并不是說做得愈多愈好，而是重在分析，務(wù)求透徹，講究質(zhì)量，提煉出解題規(guī)律和解題技巧，啟迪思維，打開思路，做到舉一反三，觸類旁通，這是培養(yǎng)和提高解題能力的關(guān)鍵．一個卓越的教師，必須要時常反思，不斷總結(jié)，創(chuàng)建以生為本的課堂，設(shè)計適合學生的教學方案，實現(xiàn)知識與技能、過程與方法和情感態(tài)度與價值觀三位一體的目標，才能培養(yǎng)適應(yīng)經(jīng)濟社會發(fā)展需要的拔尖創(chuàng)新人才。

參考文獻

1 肯貝恩著.如何成為卓越的大學教師．明廷雄，彭漢良譯．北京：北京大學出版社,2011．26

2 秦允豪．普通物理學教程 熱學(第二版)．北京：高等教育出版社,2004．126

3 李洪芳．熱學(第二版)．北京：高等教育出版社,2001．109

4 趙凱華，羅蔚茵，王笑君．新概念物理題解(下冊)．北京：高等教育出版社,2009．78

5 趙凱華，羅蔚茵．新概念物理教程 熱學(第二版)．北京：高等教育出版社,2005．139

6 宋金璠．圖像討論法在熱學中的應(yīng)用．南陽師范學院學報,2008，7(9)：79

7 胡盤新．大學物理解題方法與技巧(第二版)．上海：上海交通大學出版社,2009．26

8 禹沛．T-S圖的應(yīng)用．焦作工學院學報,1998,17(6)：468

9 吳劍峰，朱琴．卡諾循環(huán)的p-V圖．大學物理,2001,20(5)：21

10 宋金璠，張萍，李根全,等．類比推理教學法在非線性物理中的應(yīng)用．大學物理,2011,30(5)：47

11 宋金璠，李根全，侯晨霞．地方綜合性大學“熱學”精品課程建設(shè)的探索.大學物理,2011,30(7)：37

12 張寅靜，周鐵奇．熱機循環(huán)極限效率的圖像討論法．大學物理, 2005,24(7)：24

13 李椿，章立源，錢尚武．熱學(第二版)．北京：高等教育出版社,2008．99

14 宋峰，常樹人．熱學習題分析與解答．北京：高等教育出版社,2010．176