多角度審視過山車問題
——以運動學物理量解決動力學問題初探
麻志洪 陳亞琳
(浙江師范大學數理與信息工程學院 浙江 金華 321004)
1 過山車運動問題
日常生活中,我們經常有看到游樂園里的過山車從軌道上進行360°的大旋轉,極為驚險刺激.但是,如果仔細思考,我們可以抽象出這樣一個問題.
在忽略空氣阻力條件下,過山車在軌道的上半部分某一點處速度至少達到多少時,過山車不會從該點掉下?
現將物理現象抽象為物理問題.如圖1所示,位于豎直平面內的光滑圓形軌道,半徑為R,一質量為m的小球在圓形軌道上運動,若小球能夠通過圖中P(x0,y0)位置不掉下(忽略一切阻力),設此時小球的速度為v,問v至少為多少?
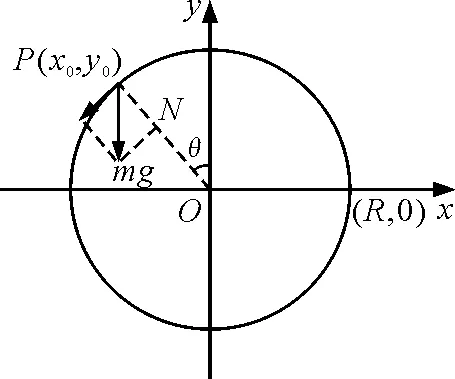
圖1
2 多種解法
(1)運用牛頓運動定律求解
設此時軌道對小球的壓力為N,小球與坐標軸原點的連線與y軸的夾角為θ.則

其中,N=0為臨界狀態.

解得
創新點:運用牛頓運動定律形式簡單,運算簡便,具有相當大的優越性,同時也是學生常用的解法.
(2)運用矢量的方法求解
如圖2,假設P點以上軌道不存在,小球將做斜拋運動,根據斜坐標法,斜拋運動可以等效成豎直方向的自由落體運動與沿著v方向的勻速直線運動.
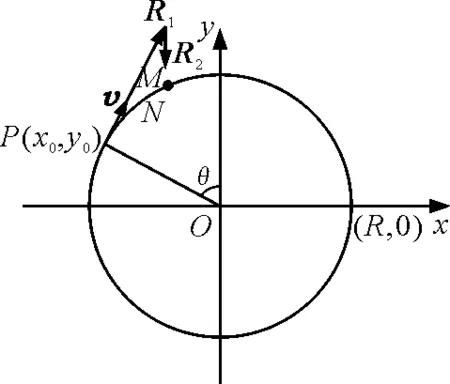
圖2
設小球在P點開始做斜拋運動,經過很小的一段時間t(t→0),則小球沿著v方向的位移矢量大小為R1,同時自由落體的位移矢量大小為R2,R1在豎直方向上的投影為R1cosθ,可得表達式
M(y)=R1sinθ-R2+Rcosθ
同時,與M橫坐標相同的N點縱坐標為
要使小球不從軌道上掉下,只需要
M(y)≥N(y)
即得到表達式
(1)
將式(1)展開并化簡可得
因為t→0,所以,令
要使該函數在t→0時大于零,則根據函數極限知識,解得
創新點:通過矢量的觀點解決該問題,雖然運算上稍加復雜,卻從一定程度上提示我們,這一問題是有其他解法的.
(3)對解法2的另一種闡述
我們可以通過解出使小球不能在軌道上的運動時的速度來解出答案.當小球不能在軌道上運動時,小球將做斜拋運動.
將速度v分解成水平方向vx與豎直方向vy.只需小球在很小一段時間內豎直方向上的上升高度小于因小球水平方向移動時圓上增加的高度,小球將不能沿著圓軌道運動.
只需要ΔH1≤ΔH2,即可解出小球不能沿軌道運動的速度.

圖3
后面的解法與解法2相同,再取v的在正實數的補集即解出答案,在此不做闡述.
創新點:此解法雖與解法2大體相同,但采用不同的速度分解方式亦體現出物理學不同的思考方式就有不同的物理解釋.
(4)當小球位于P點時,P點在軌跡A上的右導數小于在軌跡B(即圓軌道上)上的右導數,由微分知識可知,存在區間(x1,x2)曲線A將位于曲線B下方,即小球將會脫離圓軌道.
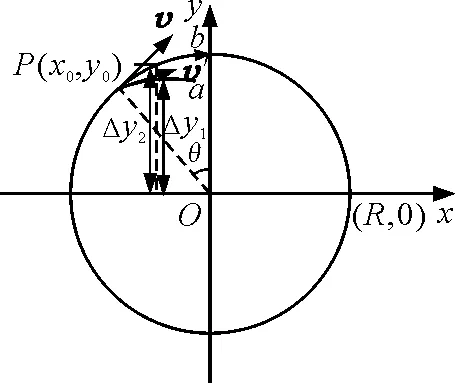
圖4
當時間取極限t→0時,P點在軌跡A上的右導數與離P點無限接近的軌跡A上的F點的切線斜率相等,同理,在軌跡B上的右導數與離P點無限接近的軌跡B上的M點的切線斜率相等,又已知軌跡A的切線方向即小球的速度方向,則當小球在P點剛好沿著A軌道運動時,在很小一段時間Δt后,速度傾斜角將小于對應相同橫坐標圓上點的切線傾斜角.設v的傾斜角為α,t時間后切線的傾斜角為β,設圓的方程為x2+y2=R2,在P點對應的圓的方程為
可列出表達式
(2)
(3)
由極限知識可知,當小球不能沿著軌道運動時只需
tanα≤tanβ
將式(3)、(4)代入,因為t→0,略去高階無窮小,可得
-2Rv3tsinθcos3θ<
2Rv3tsin3θcosθ-2vgtsinθcos2θR2
進一步化簡并取v正實數上的補集即得出答案
創新點:通過做向心運動后速度傾斜角與圓切線傾斜角的關系得出答案也不失為一種方法.
(5)通過運動學方法,運用曲率知識進行求解.
數學知識補充:
其中,k為曲率半徑,有
通過上述數學知識,可尋求y=y(x)的關系式,將物理問題轉化為數學問題.
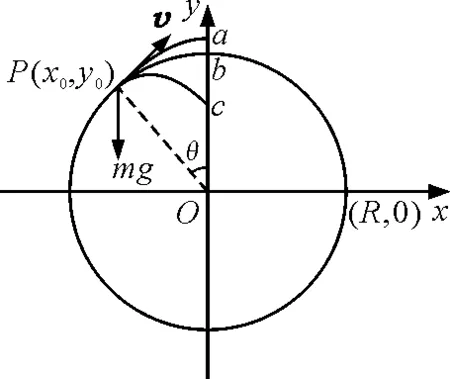
圖5
假設P點以上軌道不存在,則小球在P點以后將有3種情況:
1)沿著路徑c小球將會下落,不能沿著軌道運動;
2)沿著圓弧路徑b,小球剛好能沿著軌道運動;
3)沿著路徑a運動,則小球將會飛出軌道,此時也就是小球在P點的曲率半徑大于圓的半徑,列出小球的運動方程則有
x-x0=vtcosθ
聯立得
所以

得
創新點:運用運動學知識結合曲率公式,也較為巧妙地解決動力學問題.
解法總結:從以上5種方法我們可以發現很有意思的一個物理現象,方法1利用加速度解題,方法2利用位移解題,而方法3利用速度解題,這幾個物理量也正是運動學中最關鍵的物理量,均可作為解題思路,由此可見物理學體系的統一性.
3 多解過山車問題的思考
在物理的學習中,思維處于核心地位,而本節“一題多解“方法在一定程度上體現創新理念,注重各物理量既有聯系又有差別的理念建立過程,注重科學的研究方法,應用全方位知識解決實際問題。
從創新思維的可行性入手,為問題的深入理解提供可靠的條件.在總體上,注意緊緊圍繞學習目的,循序漸進地從提出問題,建立模型、全方位尋找方法去解釋一些物理現象,以增強自身理性知識為突破口,走出思維定勢的陰影,奔向創新的陽關大道.
參考文獻
1 程君妮.開放實驗與學生創新思維培養模式之初探.物理通報,2011(2)
2 陳禮,關偉.過山車動力學建模與仿真.中國工程機械學報,2010(4)
3 趙堅.機械能守恒定律理解中一個值得重視的問題.物理通報,2006(6)

