逐差法和Origin8.0軟件在牛頓環實驗數據處理中的比較*

唐春紅 唐曙光 劉揚正

(南京工程學院基礎部 江蘇 南京 210067)

1 引言

逐差法是物理實驗中常用的數據處理方法之一，尤其在處理一系列等間距依次變化的測量數據時，把所有數據分成前、后兩組再將對應項相減，既充分利用了所有測量數據，又具有對數據取平均和減少相對誤差的效果，在研究數據與應變量之間的函數關系時有其獨特的優點，但該數據處理方法往往非常費時，且容易出錯．隨著現代教育的發展，大量的實驗數據和圖像都可以通過計算機應用軟件進行分析和處理，能使學生從繁瑣的數據推導和計算中解脫出來，提高了學生的學習效率．簡單易學、操作靈活、功能強大的Origin8.0軟件在教學、科研、工程技術領域有非常廣泛的應用[1]，在大學物理實驗中適當地介紹這種基于Window平臺的數據分析和圖形可視化繪圖軟件，對于學生后續數據處理能力的培養起到一個拋磚引玉的作用．

本文以Origin8.0軟件用于牛頓環實驗數據處理為例，并與逐差法進行比較，使用Origin8.0軟件能快速處理與分析實驗數據．

2 實驗原理

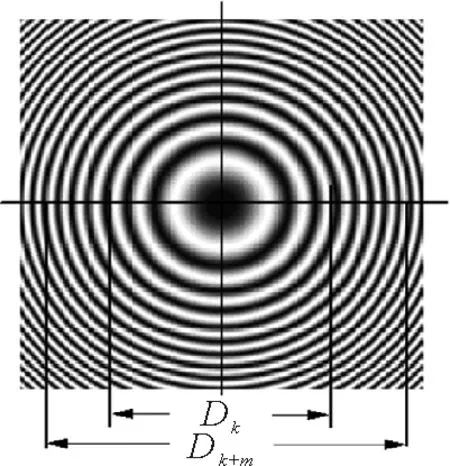
圖1 等厚干涉條紋-牛頓環

很難準確判定各干涉條紋的級次，為此在實驗中一般采用k測級圓環的直徑Dk和k+m級干涉圓環的直徑Dk+m，則

有

所以

只要測出Dk和Dk+m，知道級差，并已知光的波長λ，便可計算R．

3 實驗數據及處理結果比較

3.1 實驗數據

本實驗原始數據來源于教師的備課，數據及部分數據處理見表1.

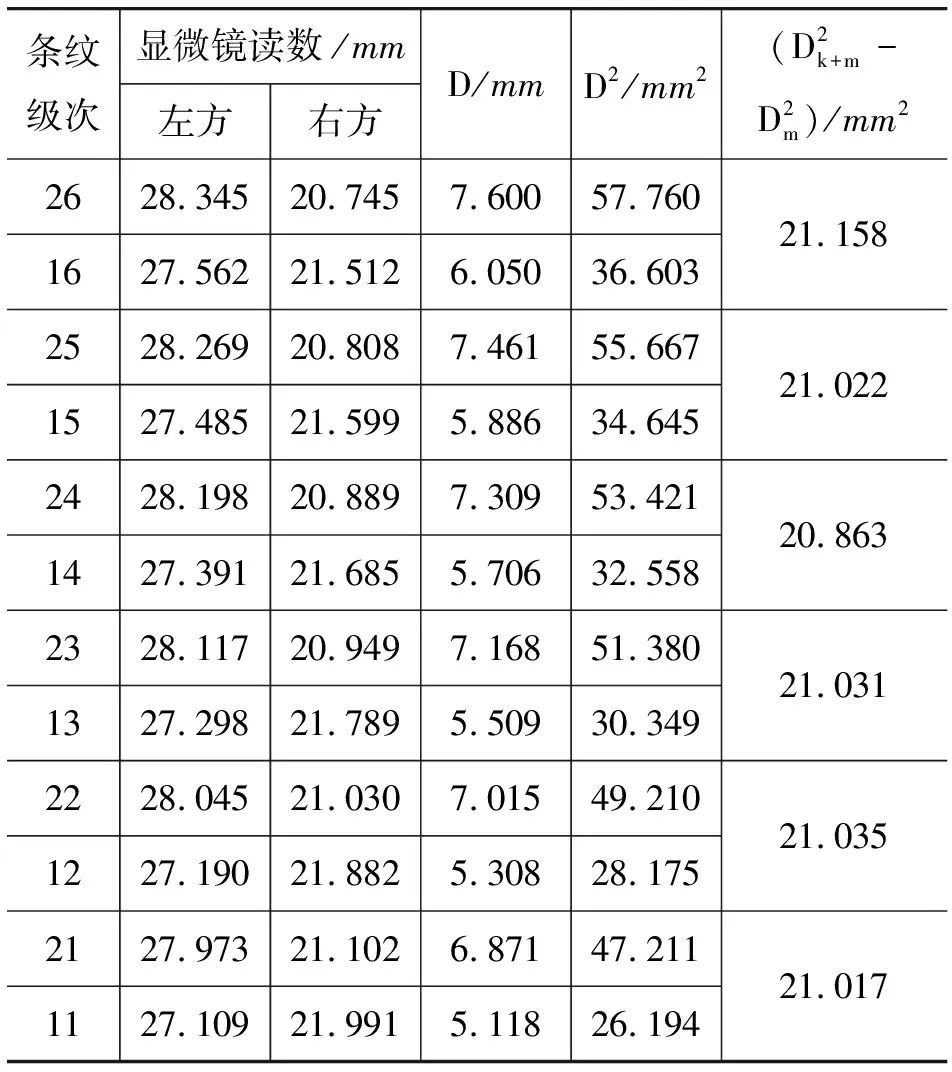
表1 牛頓環測量數據m=10,λ=5.893×10-4mm

3.2 逐差法處理實驗數據

逐差法處理實驗數據一般來說要求滿足兩個條件：

(1)函數具有的線性y=kx+b或者有多項形式；

(2)自變量是等間距變化．本實驗教材上采用逐差法處理實驗數據[2]．

用逐差法求R及R不確定度的計算．

21.031+21.035+21.017) mm2=21.021 mm2

逐差法處理實驗數據的結果是

R=(891.8±3.976) mm≈(892±4) mm

相對不確定度為

3.3 Origin8.0處理實驗數據[3]

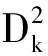
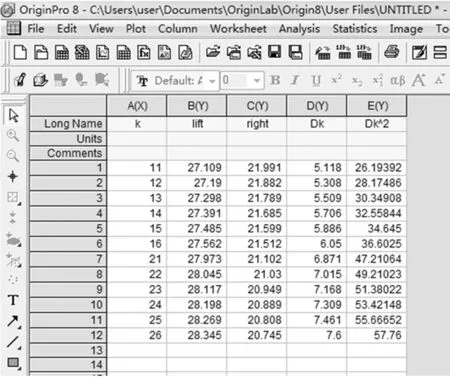
圖2 Origin工作表

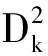
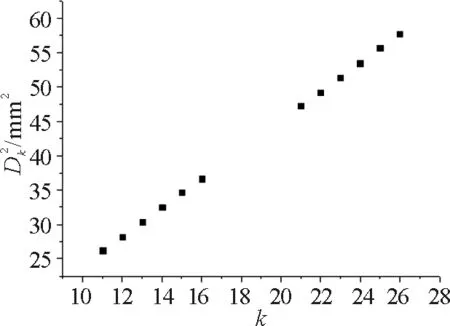
圖3 k-散點圖

擬合直線：繪出散點圖后，選擇Analysis菜單中的Fit Linear，即可對圖1進行線性擬合，Graph1中新增一條擬合出來的直線，見圖4，同時彈出結果窗口Results Log，顯示擬合結果．

圖4 線性擬合圖

圖4中左上角點表示數據散點圖，線表示擬合的直線，右下角為彈出的結果窗口，即為擬合的參數，擬合參數見圖5.

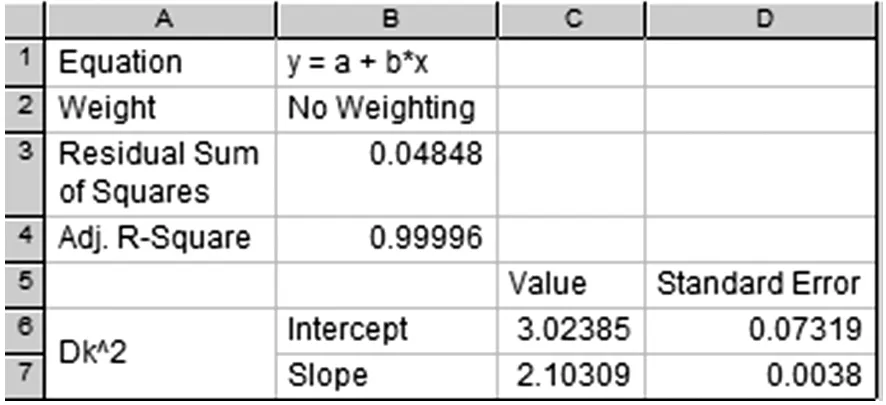
圖5 擬合參數

從圖5可以看出，直線的回歸方程y=a+bx，參數a和b分別為截距、斜率．由Results Log窗口信息可知擬合直線的截距為a=3.023 85，其標準差為0.073 19，斜率為b= 2.103 09, 標準差為0.003 8，線性擬合相關常數R=0.999 6，說明所測量的數據其擬合直線幾乎全部通過數據點．

Origin8.0處理實驗數據的結果是：

由方程4Rλ=b=2.103 09得R=892.2 mm，標準偏差為0.048 48 mm，相對不確定度為ER=

0.38%．

3.4 兩種數據處理方法的結果比較

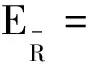
4 結論

通過Origin8.0軟件處理用牛頓環實驗數據，并與教材使用的逐差法處理實驗數據進行比較，充分體現了用計算機軟件處理實驗數據簡化了數據處理過程，提高了實驗結果的準確度，也避免了人為因素(操作不規范等)所造成的誤差，在物理實驗數據處理過程中有顯著的應用價值．

參考文獻

1 李曉波 ，謝志遠．Origin作圖在大學物理實驗教學中的應用及評價. 襄樊學院學報,2010(8):86～88

2 唐曙光．大學物理實驗.北京：科學出版社，2011.126～130

3 王曉雄．利用Origin擬合方法處理牛頓環實驗數據，大學物理實驗，2011(4):73～74