基于MF－DCCA方法的證券市場間交叉相關性研究

曾志堅，張倩倩

（湖南大學 工商管理學院，湖南 長沙 410082）＊

一、引 言

2012年6月29日簽署的《〈內地與香港關于建立更緊密經貿關系的安排〉補充協議九》指出“內地將支持符合香港上市條件的內地企業赴香港上市，為內地企業特別是中小企業到境外市場直接上市融資創造便利條件，同時積極研究降低香港金融機構申請合格境外機構投資者資格的有關資質要求，為香港有關長期資金投資內地證券市場提供便利”。這無疑會使得香港市場和內地市場的聯系變得更加緊密。在此背景下，本文對上海證券市場和香港證券市場間的交叉相關性進行探討，一方面有利于投資者了解證券市場間的聯動關系及信息傳遞，為投資者做出決策提供參考意見，另一方面，對防范金融風險的傳染，維護證券市場持續、健康發展也有著積極作用。

二、相關文獻綜述

關于證券市場間的交叉相關性，學者們最初主要運用Granger因果檢驗、動態條件相關模型（DCC）和Copula模型等進行研究。Parsva和Lean利用Granger因果關系檢驗證實了科威特等6個中東國家股票市場和外匯市場間存在因果關系［1］。Lee運用Granger因果檢驗和協整檢驗對匯改之后的中國匯率市場和香港股票市場進行分析，發現兩個市場之間存在單向Granger因果關系［2］。潘越通過非線性Granger因果檢驗進行研究，結果表明A股和H股之間一直存在因果關系［3］。董秀良和吳仁水運用DCC－MGARCH模型，發現滬深A、B股市場的相關系數總體為正，但數值較小，并具有明顯的時變特征［4］。Xiao和Dhesi利用DCC模型進行研究，結果表明英國、美國、法國和美國四個證券市場間存在顯著的時變相關性［5］。Arouri和Bellalah等通過建立DCC－GARCH模型，發現1994年后哥倫比亞等新興證券市場間的相關性顯著增加［6］。王永巧和劉詩文利用時變Copula模型進行分析，結果表明中國股市與美國、英國及日本股市保持微弱的下尾相依關系［7］。曾志堅等利用時變Copula模型發現在金融危機時期，美國證券市場對中國證券市場的波動溢出效應有增強的趨勢［8－10］。劉瓊芳和張宗益運用Copula模型檢驗了房地產和金融行業股票之間的相關關系，結果表明這兩個行業的股票在市場低迷時期的尾部相關性要大于在市場活躍時期的尾部相關性［11］。

以上研究采用的方法均建立在證券市場有效假說基礎之上，構建的是一種線性均衡的分析范式。然而，現實的證券市場是一個復雜的動力系統，時間序列往往具有非平穩和分形特征，各時間序列之間普遍存在冪律形式的交叉相關性。上述文獻中的研究方法不能很好地分析不同時間標度下時間序列的分形特征，因而無法準確描述證券市場間的交叉相關性。基于分形理論的多重分形去趨勢交叉相關分析法（MF－DCCA）能夠有效去除局部趨勢對時間序列標度的影響，可以探測不同時間標度下時間序列所呈現的分形特征，是研究非平穩時間序列之間長期冪律交叉相關性的有效手段。因此，本文擬采用MF－DCCA方法研究上海和香港證券市場間的交叉相關性。

三、實證研究設計

（一）樣本選取與數據來源

選取上證綜合指數和恒生指數分別代表上海證券市場和香港證券市場的走勢。由于2006年5月《上市公司證券發行管理辦法》施行后，H股企業紛紛回歸A股市場，到2006年12月31日，H股企業回歸A股市場達到一個高潮。因此，本文選取的樣本時間跨度為2007年1月3日～2013年5月31日。由于上海證券市場和香港證券市場因節假日而休市的日期有所不同，故刪除時間不一致的記錄，最終得到1510個樣本數據。數據來源于國泰安數據庫（http：//www.gtarsc.com/）。本文采用各市場的日指數收益率數據進行研究，其計算公式如下：

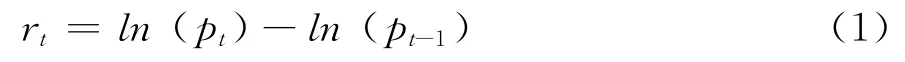
其中，rt為t時刻的收益率，pt和pt－1分別是t和t－1時刻的收盤價格。

（二）實證研究方法

首先檢驗上海和香港證券市場之間是否具有交叉相關關系，再運用MF－DCCA方法研究兩市場間的交叉相關性及分形特征。

1.交叉相關性檢驗方法。對于兩個時間序列｛xt，t＝1，2，…..N｝和｛yt，t＝1，2，…..N｝，定義其交叉相關函數為：

交叉相關統計統計量為：

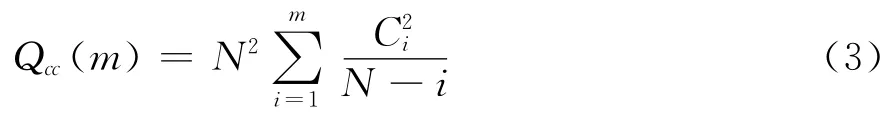
其中m是自由度，交叉相關統計量Qcc（m）則近似于自由度為m的卡方分布χ2（m）。

2.MF－DCCA方法。（1）假設兩個時間序列｛x（i）｝和｛y（i）｝，i＝1，2，..N，N是時間序列的長度，構造新的時間序列：

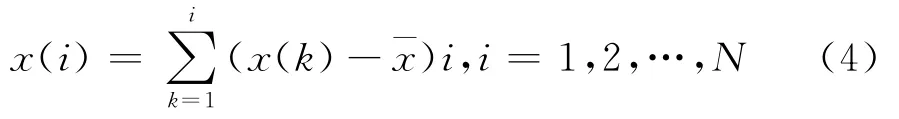
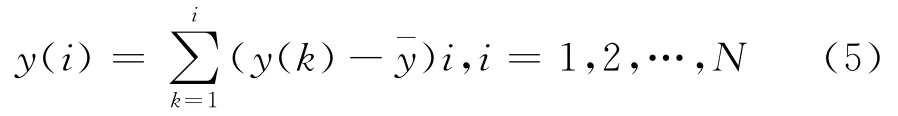
（2）把時間序列｛x（i）｝和｛y（i）｝分成Ns＝int（N/s）個不相重疊的子區間，每個子區間的長度為s。因為長度N可能不是子區間長度s的整數倍，為了能保證序列結尾的N－Ns×s的值也考慮在內，對時間序列的逆序做同樣的處理。這樣就可以得到2Ns個子區間。

（3）在每一個子區間v中，通過最小二乘法用多項式函數xv和yv擬合輪廓，對于v＝1，2，……Ns，局部協方差函數為：

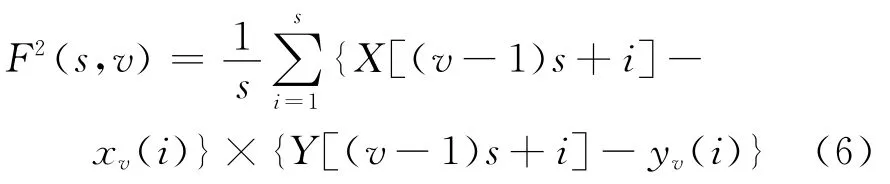
對于v＝Ns＋1，……2Ns，局部協方差函數為：

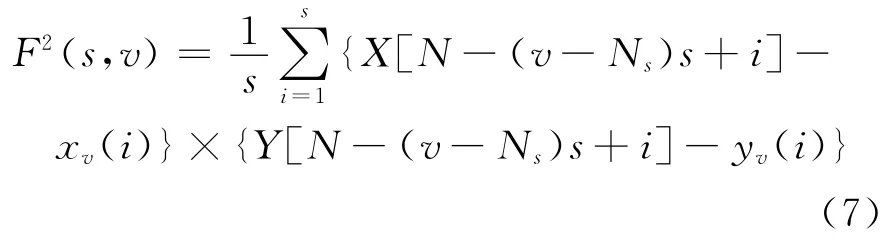
（4）把所有子區間的局部協方差取均值，可得到q階波動函數：

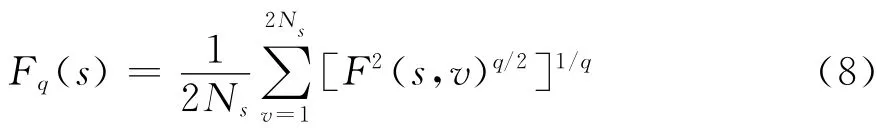
一般來說，q可以是非零的任意實數。當q＝0時，由洛必達法則得：

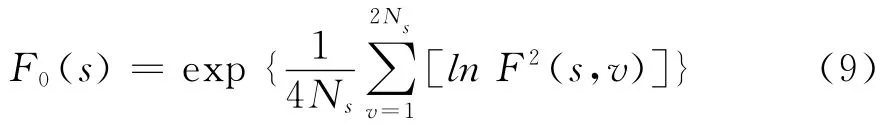
（5）計算不同標度s所對應的波動函數Fq（s）。如果兩個序列之間存在長期冪律交叉相關性，則波動函數Fq（s）和時間間隔s存在以下標度關系：

其中，標度指數Hxy（q）即為廣義赫斯特指數，是ln（Fq（s））～lns函 數 關 系 圖 的 斜 率。通 過MF－DCCA得到的廣義赫斯特指數Hxy（q）與多重分形標度指數τ（q）關系如下：

通過Legendre變換，可以得到描述多標度時間序列的多重分形譜f（α）：

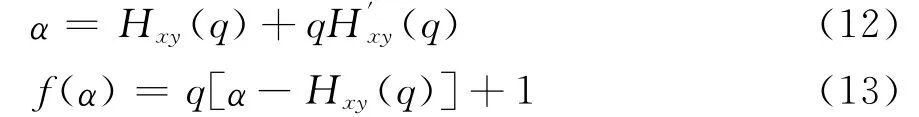
其中，α為奇異指數，用來描述時間序列的奇異程度。f（α）為多重分形譜，它的值反映了具有奇異指數α的分形維數。

四、實證結果分析

（一）交叉相關性檢驗結果分析

首先驗證上海和香港證券市場間是否存在交叉相關關系。自由度m的取值范圍是從1～1000，對于不同的自由度m，分別計算其相應的交叉相關統計量Qcc（m）和卡方分布χ2（m）的臨界值。

圖1 交叉相關性檢驗Qcc（m）

圖1中實線表示交叉相關性統計量Qcc（m），虛線表示自由度為m，顯著性水平為5%時卡方分布x2（m）的臨界值。從圖中可以看出，在自由度從1～1000范圍內，交叉相關性統計量Qcc（m）均大于相應的卡方分布x2（m）的臨界值，這表明上海和香港證券市場之間存在顯著的交叉相關性。

（二）MF－DCCA結果分析

進一步利用MF－DCCA方法準確量化上海和香港證券兩個市場之間的交叉相關性，設定時間標度s的取值范圍是從10～N，N為時間序列的長度，q的取值為q＝5，4，……－4，－5。

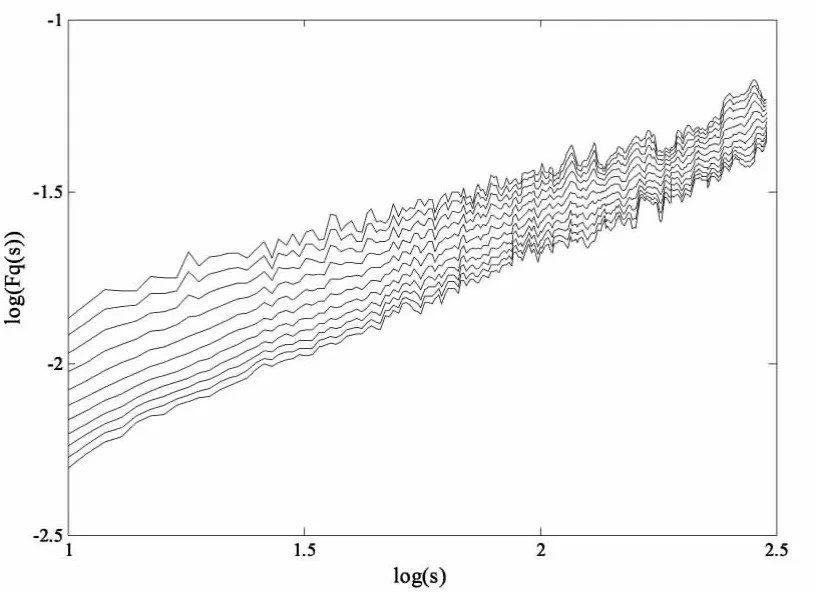
圖2 上海與香港股票市場收益率序列的雙對數波動曲線圖

從圖2可以看出，對于不同的q，其波動函數Fq（s）和時間標度s之間都表現出較好的冪律關系，即上海和香港證券市場之間存在著交叉相關性。這表明上海證券市場波動的變化不僅受到自身波動的影響，也會受到香港證券市場波動的影響；而香港證券市場的波動也會受到上海和香港兩個證券市場的影響。

通過最小二乘法擬合得到上海和香港證券市場收益率序列雙對數波動曲線ln（Fq（s））～lns函數關系圖的斜率Hxy（q）（參見表1）。

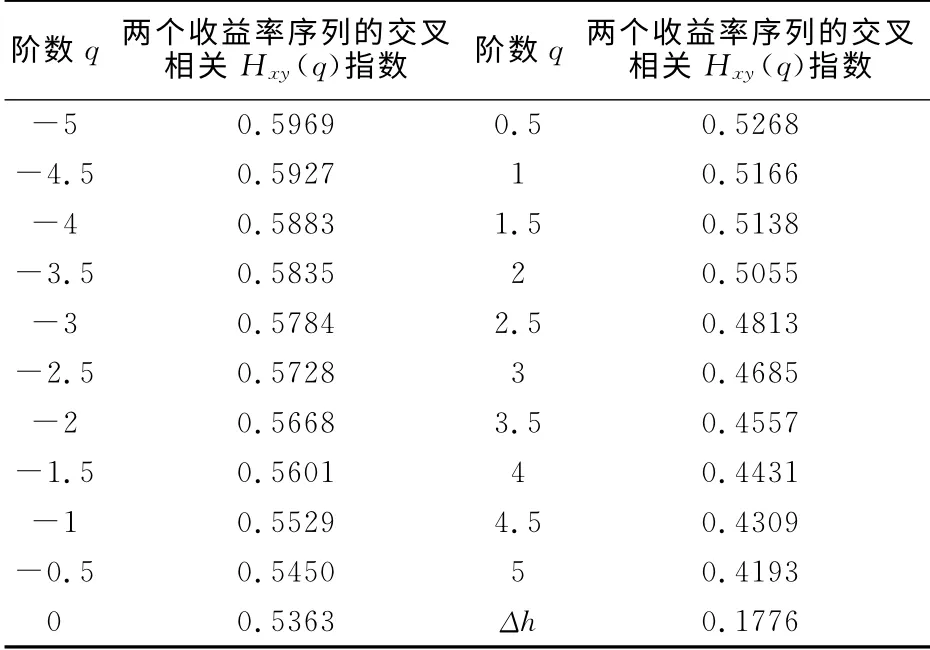
表1 股指收益率的Hxy（q）指數

由表1可以看出，當q從－5變化到＋5時，兩個證券市場的交叉相關指數Hxy（q）從0.5969遞減到0.4193。Hxy（q）是隨著q的變化而變化，不是一個固定的常數，這說明上海證券市場和香港證券市場之間的交叉相關性具有多重分形特征。這也證明了兩個證券市場間的關系是非線性的，采用正態分布、單重分形等傳統方法對這兩個市場之間的關系進行描述是不合適的，因此。需要突破傳統的線性范式，以非線性的角度來分析證券市場中的問題。因此不論是投資者還是監管者都應該將這兩個市場當作一個整體來考慮，僅僅考慮其中一個市場，而忽略另外一個市場，會導致對證券市場的理解產生偏差。

產生多重分形的原因主要來自兩個方面：一是由于證券市場上存在的長程相關性；二是由于證券市場時間序列的厚尾分布。長程相關性表明證券市場上出現的波動會影響未來證券市場價格的變化趨勢，市場上可能會出現連續的上漲和下跌。從表1可以發現，當q＝2時，Hxy（q）＝0.5055＞0.5，說明上海和香港兩個證券時間之間存在長程相關性，一個市場的價格對另一市場的歷史價格具有長期記憶性，即一個證券市場上出現的波動會對另一個市場的未來收益產生影響。

時間序列的厚尾分布說明，上海和香港兩個證券市場既不像有效市場假說所闡述的大幅波動出現的概率幾乎為零，也不像單一分形所描述的大幅波動和小幅波動出現的概率幾乎相等，而是不同幅度的波動具有不同的標度關系，即大幅波動和小幅波動出現的概率以及具有的風險程度都是不同的。投資主體對成堆信息的非線性處理方式將導致厚尾分布的出現。一般而言，當頒布某項新政策時，大部分投資者不會及時地對此做出反應，只有當信息累積到一定程度，才會做出決策。這就使得市場上出現的信息不能立即被投資者消化，相反會形成某種程度的累加效應，導致“羊群效應”、“追漲殺跌”等現象的出現。

從圖3可以看出，當q＜0時，上海和香港證券市場之間的交叉標度指數要小于兩個市場的平均標度指數，即兩個市場的交叉相關性要小于其自相關性。而當q＞0時，上海和香港證券市場之間的交叉標度指數要大于兩個市場標度指數的均值，即兩個市場的交叉相關性要大于其自相關性。這就說明短期內當某一個市場出現較大波動時，很可能是由于另外一個證券市場的動蕩所引起的，而不是因為市場自身原因所引發的。比如在由美國次貸危機引發的全球金融危機中，由于香港證券市場開放程度較高，受到嚴重影響，股價大跌，出現大幅波動。而香港市場和大陸市場之間的聯系緊密，使得危機進一步傳染到了上海證券市場，從而引發了上海證券市場的波動。

進一步依據式（11）～（13）分析上海證券市場和香港證券市場間交叉相關性的多重分形特征。為了能更清楚地描述不同q值下標度指數τ（q）的變化過程，將q值的范圍放大，選取－100≤q≤100，步長為10。

從圖4可以看出，標度指數τ（q）是關于q嚴格單調遞增的凸函數，τ（q）與q之間存在明顯的非線性關系。這再次表明上海和香港證券市場市場間交叉相關性存在多重分形特征。

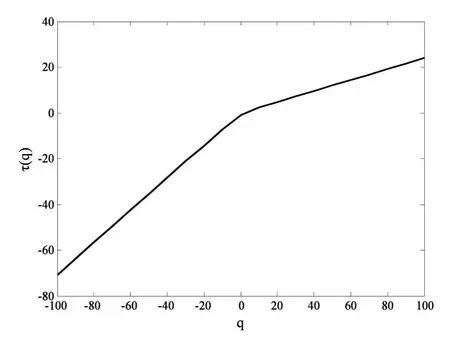
圖4 上證指數和恒生指數收益率τ（q）與q關系圖

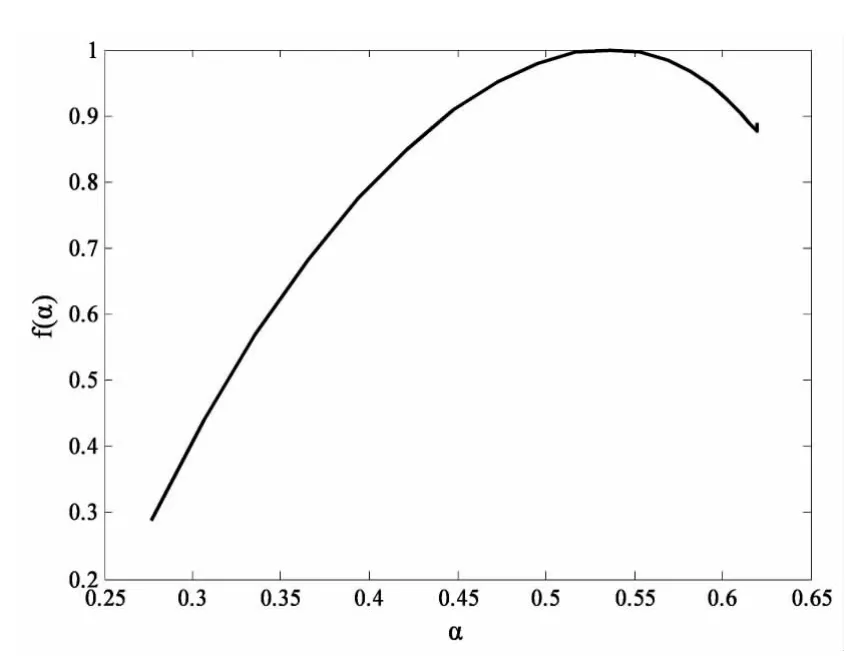
圖5 上證指數和恒生指數收益率f（α）與α關系圖

圖5是多重分形譜f（α）與奇異指數α關系圖。從整體來看，f（α）曲線頂部較平坦，開口寬大，曲線分布在較大的范圍內。從具體數值來看，f（α）在α等于0.276885時達到最小值0.2879，在α等于0.5363時達到最大值1，f（α）是隨著奇異指數α值的變化而變化。多重分形譜中奇異指數α的最大值為0.619135減去最小值0.276885，即得到多重分形譜寬度Δα＝0.343113。同標度指數τ（q）曲線結果一樣，這也進一步表明了上海和香港證券市場的交叉相關性具有多重分形特征。

五、結 論

以上運用MF－DCCA方法進行研究，發現上海和香港證券市場之間存在顯著的長程交叉相關性，且呈現出多重分形特征。一方面，說明上海和香港證券市場不僅會受到市場自身的波動而發生變動，還會受到彼此波動的影響。另一方面，表明投資者是以非線性的方式對市場信息做出反應，只有當信息累積到一定程度時，才會對信息進行處理，從而導致“羊群行為”等非理性行為的發生。因此，對投資者而言，在進行決策過程中，應該把上海證券市場和香港證券市場當作一個整體，全面考慮兩個證券市場出現的波動對未來收益的影響，更好地規避投資風險。對金融監管者而言，同時，也應該加強對上市公司信息披露的監管，減少信息的不對稱性，不斷提高市場運行效率。同時也應加強對投資主體的理性投資教育，優化投資者結構，改善市場投資主體的構成，發揮機構投資者的理性投資作用，促進證券市場的長期健康發展。

［1］Parsva P，Lean H H.The analysis relationship between stock prices and exchange rates：evidence from six middle easter financial markets［J］.International ResearchJournal of Finance and Economics，2011，（66）：157－171.

［2］Lee W C.A Study of the causal relationship between real exchange rate of Renminbi and Hong Kong stock market index［J］.Modern Economy，2012，（3）：563－566.

［3］潘越.基于非線性Granger因果檢驗的股市間聯動關系研究［J］.數量經濟技術經濟研究，2008，（9）：87－100.

［4］董秀良，吳仁水.基于DCC－MGARCH模型的中國A、B股市場相關性及其解釋［J］.中國軟科學，2008，（7）：125－133.

［5］Xiao L，Dhesi G.Volatility spillover and time－varying conditional correlation between the European and US stock markets［J］.Global Economy and Finance Journal，2010，3（2）：148－164.

［6］Arouri M E H，Bellalah M，Nguyen D K.The comovements in international stock markets：new evidence from Latin American emerging countries［J］.Applied Economics Letter，2010，（17）：1323－1328.

［7］王永巧，劉詩文.基于時變Copula的金融開放與風險傳染［J］.系統工程理論與實踐，2011，31（4）：778－784.

［8］曾志堅，徐迪，左楠.金融危機對證券市場波動溢出的影響研究［J］.財經理論與實踐，2011，32（174）：48－52.

［9］曾志堅，范麗，周競東.基于互譜分析的權證與標的證券收益率波動溢出研究［J］.財經理論與實踐，2010，（6）：38－43.

［10］曾志堅，鐘紫璇，曾艷.中國創業板和主板市場間溢出效應分析［J］.財經理論與實踐，2012，（6）：43－47.

［11］劉瓊芳，張宗益.基于Copula房地產與金融行業的股票相關性研究［J］.管理工程學報，2011，25（1）：165－1689.