IEEE接地設計標準與我國接地設計標準的異同分析
胡慶來,李漢峰
(中南電力設計院,武漢市430071)
0 引言
目前,隨著中國國際貿易往來的增多,國內各大工業集團與設計院參與承包和設計的涉外工程也與日俱增,而許多國外工程在標書或合同中都要求接地設計采用國際標準,其中要求最多的就是采用美國的IEEE標準。
國內設計院在電廠和變電站接地設計中長期習慣使用DL/T 621—1997《交流電氣裝置的接地》標準(下稱我國標準),它與美國的IEEE接地設計標準在內容及算法上都存在差異,而且IEEE標準為全英文版,給國內設計人員在處理涉外工程的接地網設計上帶來了不少困難。
因此,就電力系統接地設計中通常采用的電力行業標準DL/T621—1997與IEEE標準中最常用的、涉外工程業主最關注的幾個方面進行論述和對比,希望能給火電廠、變電所工程的接地設計,尤其是涉外工程的接地設計提供參考和借鑒。
1 接地裝置導體截面的選擇方法比較
1.1 IEEE標準中接地裝置導體截面選擇和計算方法
IEEE Std 80—2000[1](下稱 IEEE 標準)中規定,接地系統的每一個元件,其設計選擇都應滿足裝置的預期設計壽命,在最不利的故障和持續時間的共同作用下,應能避免熔化和機械損傷[2]。
IEEE標準中規定,按滿足避免熔化條件選擇的接地裝置導體最小截面為
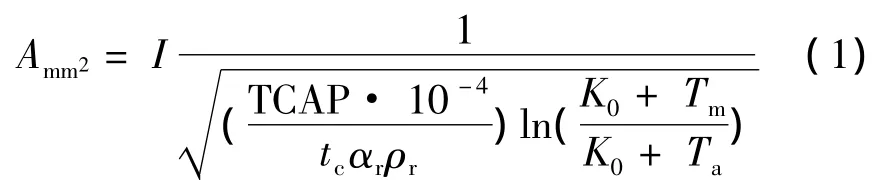
式中:I為流過接地裝置導體的入地短路電流有效值,kA,應根據系統最大運行方式確定;Tm為最高允許溫度;Ta為接地材料參考常態溫度;TCAP,αr、K0、ρr為各種溫度不同材質下的系數;tc為短路電流持續時間,s;當配有2套速動主保護時,取主保護動作時間、斷路器失靈保護動作時間、斷路器開斷時間三者之和;配有1套速動主保護時,tc取斷路器開斷時間與第1級后備保護的動作時間之和,s。應注意,如涉外合同另有規定時,應遵守合同要求。
采用式(1)計算的基本假設條件是,發生短路過程中所有的熱量都留在導體中,即為絕熱過程。對于大多數金屬,只要故障時間在幾s內,在相當寬的溫度范圍,這些假設都是適用的[3]。
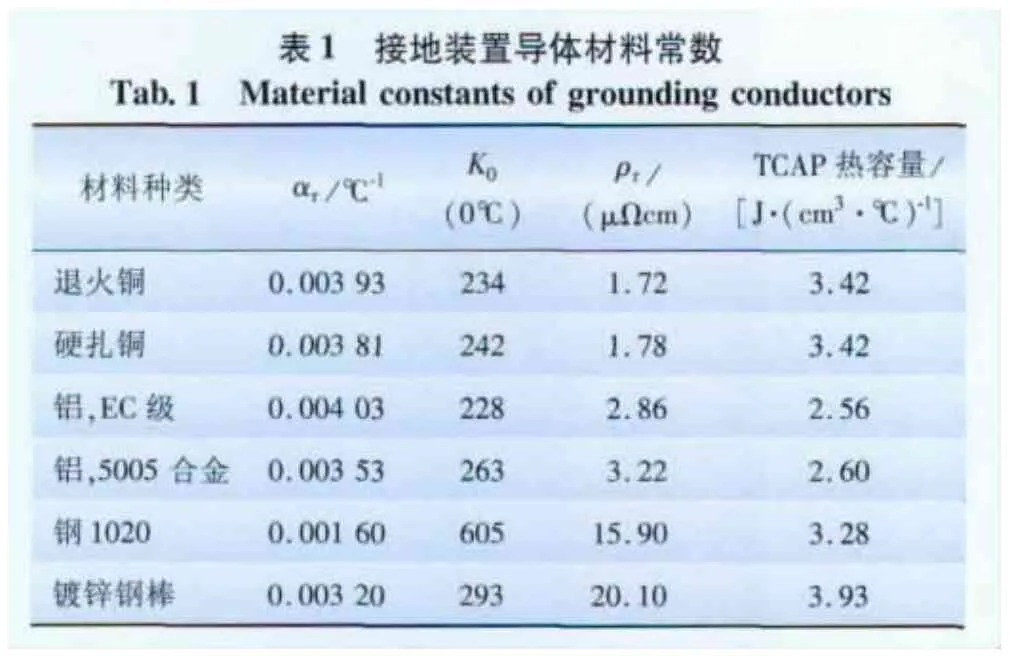
IEEE標準中采用表格的形式給出了一些接地材料特性參數(主要以Tr=20℃為基準進行計算,見表1)。
?
應注意,當故障電流為非對稱電流即短路電流中存在直流分量(非周期分量)情況下,需將非對稱電流If折算成等效對稱電流IF(IF=If×Df),Df為衰減系數;然后再代入前面IEEE標準的公式進行計算。在考慮直流分量(非周期分量)情況下,選擇的導體將會更大一些。
將各種接地材料的固有屬性、材料常數代入IEEE標準的導體截面選擇公式中,可以得到如下簡化形式:
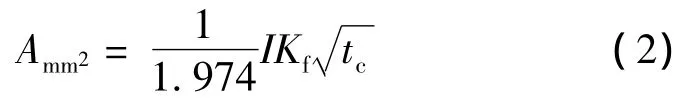
式中Kf是材料在不同Tm值(指熔化溫度或根據條款IEEE 11.3.3的導體限制溫度)下的常數。
1.2 我國標準中接地裝置導體截面選擇設計和計算方法
按照我國現行電力行業標準DL/T 621—1997[4]中附錄C中的定義,根據熱穩定條件,未考慮腐蝕時,接地裝置導體的最小截面應符合下式要求:

式中C為接地線材料的熱穩定系數。
根據我國標準的規定,按熱穩定條件,接地裝置接地極(指接地網內的導體)的截面選擇上不宜小于連接至該接地裝置的接地線(也就是接地引下線)截面的75%。這是因為從設備到地網的引下導體要承受流入地網的全部故障電流,而地網通過分流使地網中的每段導體只承受部分故障電流。引下導體就應該比地網導體尺寸更大或從設備到地網連接采用多條引下導體,使之有足夠的通流量來承受全部故障電流。對于傳導雷電流的接地裝置導體無須做更多的考慮,根據故障電流要求而選定的導體尺寸,通常也足以通過雷電引起的短時浪涌。
1.3 IEEE標準與我國標準中接地裝置導體截面選擇方法的異同
將IEEE標準中的接地裝置導體最小截面計算公式進行簡單變形即為
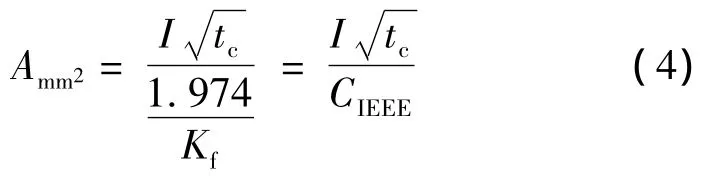
各接地材料的我國標準中熱穩定系數C和IEEE標準等效熱穩定系數CIEEE比較見表2。
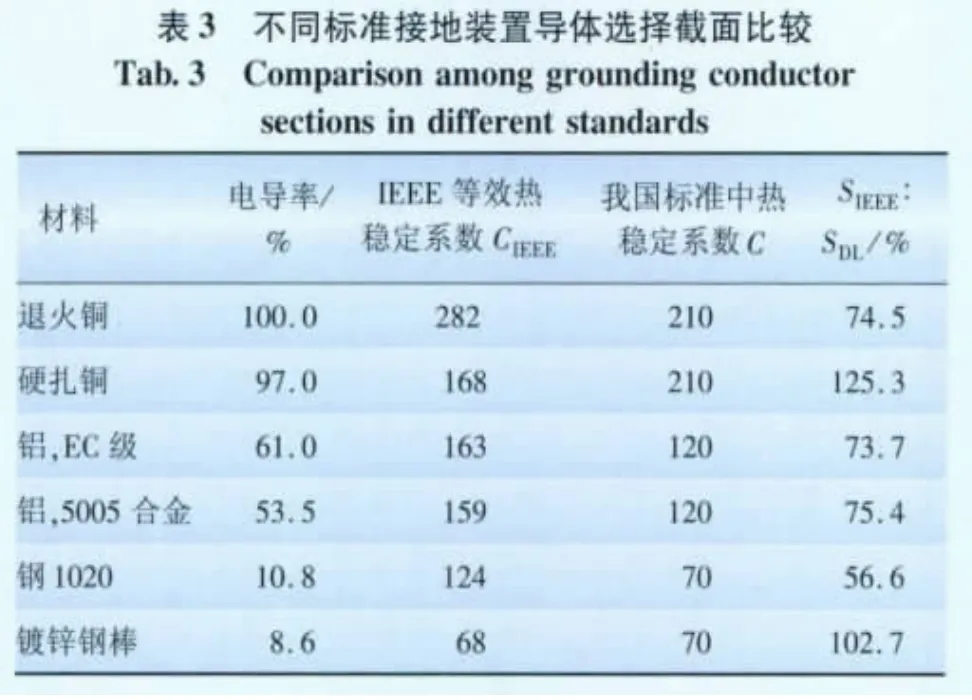
在同樣的短路電流和短路持續時間下,其選擇的接地裝置導體截面應與熱穩定系數成反比,據此,IEEE標準與我國標準選定導體截面之比見表3。

?
?
從表3可以看出,按IEEE計算,當考慮熔化溫度時,退火銅材、鋁材和普通鋼材截面小于按我國標準(熱穩定系數)選取的截面,即我國標準設計更保守一些。當計算溫度采用硬扎銅材(退火溫度為250℃)時,按IEEE標準選取的截面比我國標準選取的約大25%;采用鍍鋅鋼棒時,比我國標準選取的大3%。即對于鍍鋅鋼棒和硬扎銅材(采用退火溫度為250℃)設計時,IEEE標準的裕度更大一些。
在接地裝置的設計壽命內,導體的強度應能經受得住任何預期的機械作用或腐蝕引起的損傷。對于那些可能暴露在腐蝕環境中的接地裝置導體,即使采用了上述正確的導體尺寸選擇計算方法,也應有遠見地選擇更大尺寸的接地裝置導體,以抵補在接地裝置設計壽命周期內接地裝置導體截面逐漸減小的情況[6]。
2 接地電阻值的計算方法比較
2.1 IEEE標準中復合接地網接地電阻值的計算方法
復合接地網簡化計算法:
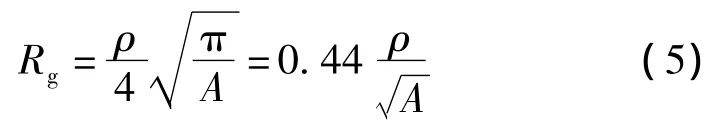
式中A為接地網的總面積,m2。
式(5)是將接地網按照等效圓盤計算[7],考慮到地網與圓盤的誤差,與接地網的長度有關,增加一個附加的修正部分,就得到如下簡化公式:
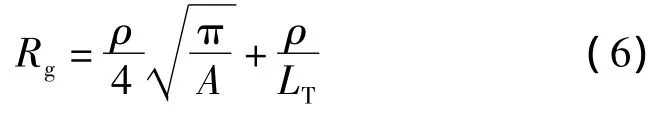
式中LT為接地裝置導體的總長度。
復合接地網的等值計算法:
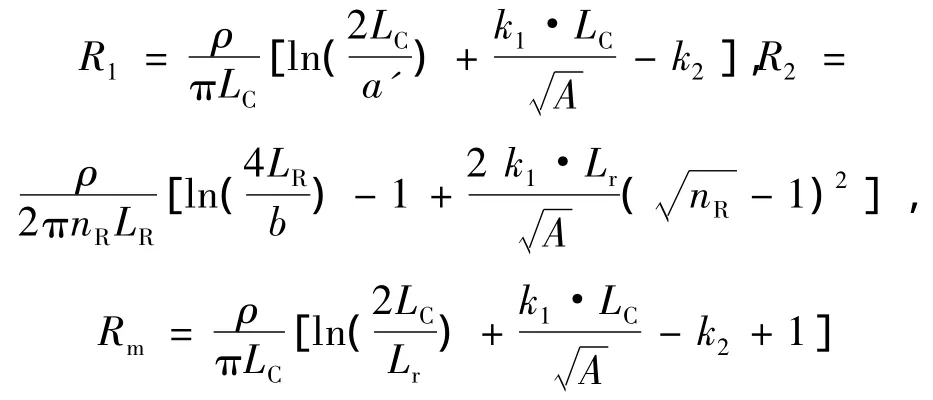
接地電阻值為
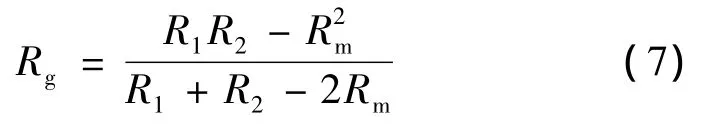
式中:LC為接地網所有接地水平導體的總長度,m;a'為接地水平導體的計算埋深,m;LR為所有垂直接地極總長,m;Lr為每根垂直接地極的長度,m;b為垂直接地極的半徑,m;nR為接地網面積區域A內的接地極數量;k1和k2是關聯系數。
2.2 我國標準中復合接地網接地電阻值的計算方法
我國標準中也介紹了復合接地網接地電阻值的簡化計算法和標準計算法。
(1)復合接地網簡化計算法。
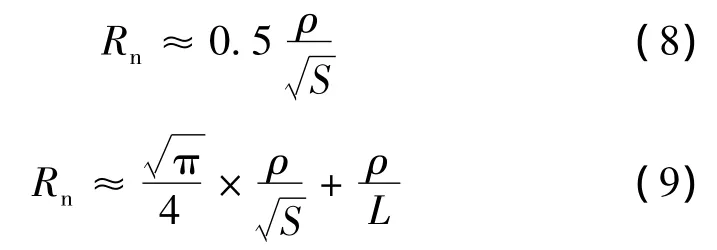
式中:S為接地網系統的總面積;L為水平接地體的總長。
(2)復合接地網等值計算法。
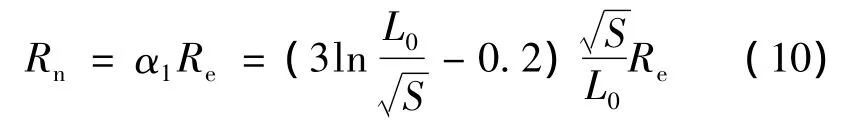
2.3 IEEE標準與我國標準中接地電阻計算方法的異同
(1)對于簡化的復合接地網電阻計算法比較。比較IEEE標準中公式與我國標準中第1種簡化公式:
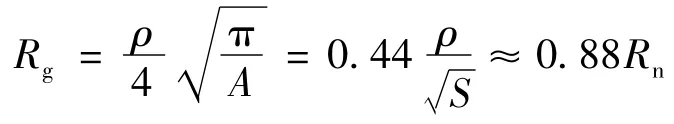
從上述情況可以看出,兩者型式上是基本一致的,但IEEE標準計算結果比我國標準偏小12%。
引入圓盤修正系數后,第2種簡化公式:
對于第2種簡化公式而言,兩者在形式是一致的,但,IEEE標準定義的LT包含所有接地裝置導體的總長度(包括水平和垂直接地體),即使這樣相加也只是保守近似的,因為在同等長度上垂直接地極將更為有效[8];而在我國標準中定義的 L僅為水平接地裝置導體的總長度。很顯然,在此情況下IEEE標準計算接地電阻將比我國標準小,我國標準的簡化計算更偏保守。
(2)對于復合接地網電阻的等值計算法比較。
IEEE標準中是采用先獨立計算出水平接地網和垂直接地極的等效電阻R1和R2,然后計算出水平地網與垂直接地極之間的相互電阻Rm,最后代入計算公式求出接地網最終的接地電阻等效值Rg。
而我國標準中的計算方法原理有所不同,是先計算出轉化為等值(即等面積、等水平接地極總長度)方形接地網的接地電阻Re,然后根據實際接地網外緣邊線的總長度算出相對于方形接地網的變化系數α1;最終算出任意形狀邊緣閉合接地網的接地電阻等效值Rn。
3 變電站有效接地系統中接觸電位差和跨步電位差要求值(限值)的計算方法比較
3.1 IEEE標準中有效接地系統接觸電位差和跨步電位差限值的計算方法
考慮人體電阻為RB=1 000 Ω。
(1)對于50 kg的人,人體可承受的接觸電位差及跨步電位差限值分別為
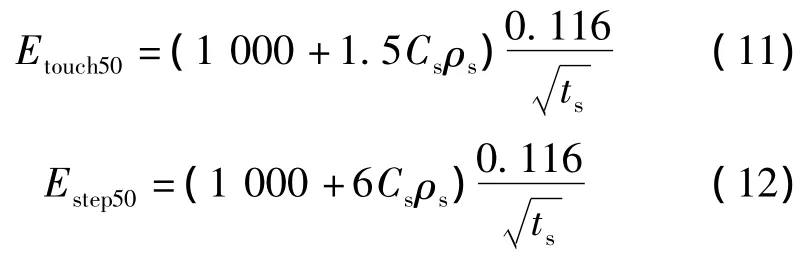
式中:Cs為在土壤的表層,為提高接觸和跨步電位差的閥值而敷設了高阻材料,考慮其影響效果的衰減折扣系數[9]。但如果沒有表面防護層,則 Cs=1,ρs=ρ。
(2)對于70 kg的人,人體可承受的接觸電位差及跨步電位差限值分別為
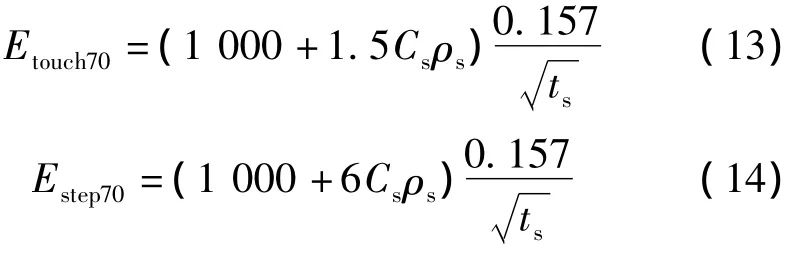
3.2 我國標準中有效接地系統接觸電位差和跨步電位差限值的計算方法
在我國標準中不區分人體體重,人體可承受的接觸電位差及跨步電位差限值的公式統一如下。
接觸電位差:
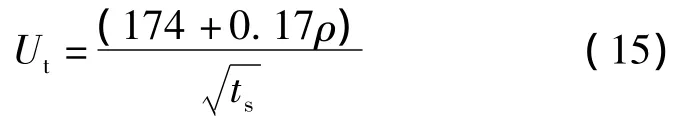
跨步電位差:
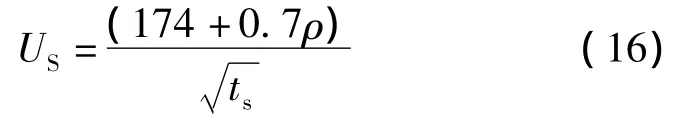
3.3 IEEE標準與我國標準中接觸電位差和跨步電位差值計算方法的異同
IEEE標準中,跨步電位差與接觸電位差公式分為體重50 kg和70 kg 2種情況考慮。從條件的苛刻性來說,如果體重取50 kg,要求值將會降低,從而條件更苛刻,這也更加符合亞洲人實際身體情況,建議設計時取人體體重為50 kg較為合適。
對于人體電阻參數而言,在IEEE標準中,選用RB=1 000 Ω,而我國標準中實際采用人體電阻為1 500 Ω。并考慮當未鋪設表面絕緣層,即無表面層土壤時 Cs=1,ρ= ρs。
對于上述情況,將人體電阻1 500 Ω、Cs=1,ρ=ρs代入IEEE標準中的50 kg人體的接觸電位差和跨步電位差公式,可以得出:
(1)接觸電位差。
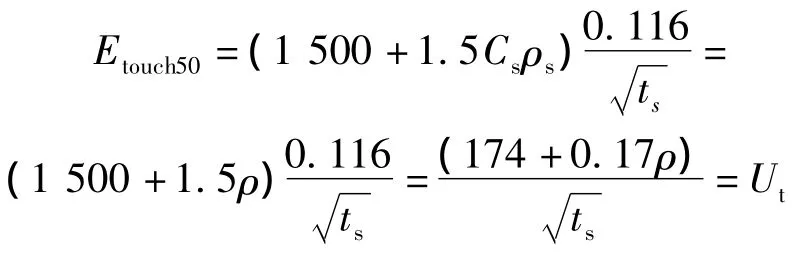
(2)跨步電位差。
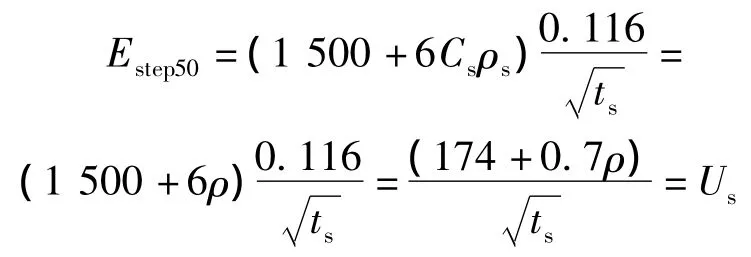
所以,我國標準中的公式是一種結合我國國情,在特定情況下IEEE標準公式的特例,即按人均體重50 kg,人體電阻為1 500 Ω,且土壤上未鋪設表面保護材料層情況下的計算值。
如果考慮土壤表面材料的衰減系數、人體電阻為1 500 Ω,IEEE標準中對于50 kg體重的計算公式即變為
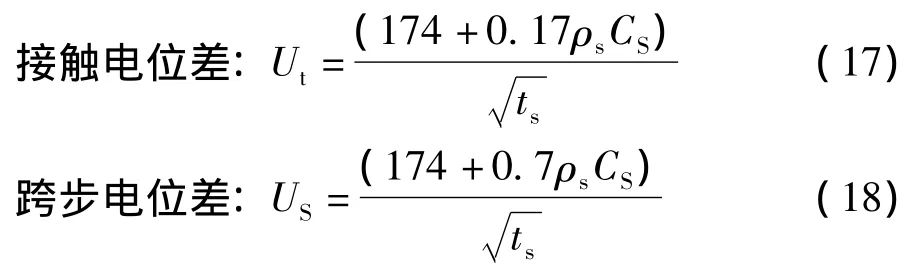
該公式也是目前國標GB 50065—2001中的推薦公式[10]。
4 結語
通過本文的具體分析和逐一對比,可以看出2個標準在應用中主要異同點。
(1)在IEEE標準與我國標準中的接地體截面選擇設計計算方面,IEEE標準更加準確和精細,它考慮了不同的使用環境、溫度系數及其他固有屬性的影響,對于同種材料不同材質也做了進一步的細分,即采用不同材質系數。而我國標準相對簡單,沒有區分各種具體材質及型號以及環境因素,只是通過規程直接查取相應的經驗系數值,準確率相對低很多,但在計算上卻較為方便。
(2)在IEEE標準與我國標準中的接地電阻計算方面,對于復合地網的計算方法在原理上兩者有所不同;而在簡化公式的計算方法上則是一致的;只是IEEE標準相對更多地考慮了如垂直接地極和接地網深度等一些必要因素。
(3)通過本文分析和公式推導,可以看出我國標準中的跨步電位差與接觸電位差(限值)計算公式,實際上是在IEEE標準的跨步電位差與接觸電位差(限值)公式基礎上,結合我國人均身體條件,并在特定情況下的一種公式形式的衍變。
[1]IEEE Std 80—2000 IEEE guide for safety in AC substation grounding[S].
[2]Natarajan R,Popoff J.Analysis of grounding systems for electric traction[J].IEEE Traction on Power Delivery,2001,16(3).
[3]Practical Applications of ANSI/IEEE Standard 80,IEEE Guide for safety[M].IEEE Tutorial Course,1986.
[4]DL/T 621—1997交流電氣裝置的接地[S].北京:中國電力出版社,1998.
[5]姜俊峰.發電廠、變電所接地設計研究[D].鄭州:鄭州大學,2004.
[6]International Electrotechnical Commission.Effects of current passing through the human body[M].IEC,1984.
[7]Schwarz S J.Analytical expression for resistance of grounding systems[J].IEE Transactions on Power Apparatus and Systems,1954,173(13):1011-1016.
[8]Joseph P,Kosiarski.The use of electrically conductive organic surface coatings shielding and grounding of plastic enclosures[J].Polymer-Plastics Technology and Engineering,1979,33(2):183-195.
[9]王洪澤.對電力標準《接地》中接地網最大接觸電位差公式的分析與拓展[J].廣西電力工程,2000(4):23-26.
[10]GB 50065—2011交流電氣裝置的接地設計規范[S].北京:中國計劃出版社,2012.

