基于符號分析的極大聯合熵延遲時間求取方法*

張淑清 李新新 張立國 胡永濤 李亮

(燕山大學電氣工程學院，河北省測試計量技術及儀器重點實驗室，秦皇島 066004)

(2012年11月30日收到;2013年2月4日收到修改稿)

1 引言

混沌自從被確認是長期可控制的和短期可預測以后，其研究課題引起了大家廣泛的興趣.然而相空間重構作為混沌時間序列處理中的重要課題，其最佳延遲時間的選取至關重要.對于時間序列X(n)，過小的延遲時間τ將導致信息的冗余，使得重構的坐標之間不可分辨，過大的τ將使延遲坐標之間毫不相關，不能代表真實的動力系統[1]，因此選取最佳延遲時間需要使X(n)和X(n+τ)最大限度相互獨立卻又不是完全無關.

確定相空間重構最佳延遲時間的方法有互信息函數法、自相關函數法和平均位移法等.其中互信息函數方法是估計重構相空間延遲時間的一種有效方法，它在相空間重構中有很廣泛的應用.Shaw首先提出互信息第一次達到最小時滯時作為相空間重構的最佳延遲時間[2]，Faster給出了互信息計算的遞歸算法.但其提出的劃分網格計算方法過于復雜，不易于編程實現及推廣使用.國內學者提出了相應的改進算法并獲得很好的應用，這在一定程度上激發了人們對準確快速地選取相空間重構中最佳延遲時間的興趣[3].文獻[4]提出了確定延遲時間變量的聯合熵之第一極大準則，相對互信息方法減少了計算量，但在求取聯合熵時采用劃分網格的方法，計算相對復雜而且誤差較大;文獻[5，6]提出了改進的網格標記法，該方法與符號分析法相比計算仍然相對復雜;文獻[7]提出的符號分析法求取互信函數，從而確定出最佳延遲時間，可避免復雜的網格劃分和標記，但需同時求取X(n)和X(n+τ)的各自信息熵及其聯合熵.本文提出了基于符號分析的極大聯合熵延遲時間求取方法，較好地解決了上述方法中所存在的各種問題，可以快速有效地提取混沌動力系統中有用定量信息，重構系統的相空間.

2 最佳延遲時間的極大聯合熵準則

考慮時間序列X(n)及其延遲時間序列Xτ(n)=X(n+τ)，n=1,2,···,N.根據互信息函數的遞推公式[8]，兩組序列的互信息可表示為

其中X代表時間序列X(n)，Xτ代表其延遲序列X(n+τ)，H(X)是孤立的 X 的不定性，H(X|Xτ)是已知Xτ的X的不定性，所以Xτ的已知減少了X的不定性，則I(X,Xτ)的第一極小值處的τ即為最佳延遲時間.并且為了計算I(X,Xτ)，Fraser和Swinney提出了復雜的劃分網格的方法[2].

互信息I(X,Xτ)表征X和Xτ的相關程度，相空間重構最佳延遲時間的確定是在保證重構坐標之間最大限度地相互獨立的基礎上提出來的.I(X,Xτ)取極小值時，X和Xτ的相關度也極小，即X和Xτ的聯合整體不確定度達到極大.

另一方面，為了保證重構坐標之間最大限度地相互獨立，應使X和Xτ聯合整體的不確定性達到最大.由信息理論可知，聯合熵H(X,Xτ)是X和Xτ的聯合整體的不確定性的度量，H(X,Xτ)越大，則X和Xτ聯合整體的不確定性也越大.由此推斷，聯合熵H(X,Xτ)的第一個極大值點即為相空間重構的最佳延遲時間點[4].

同時，混沌吸引子在其不變集具有的遍歷特性表現在其狀態變量X(n)上，即在穩態情況下，對任意的延遲時間τ，X(n)和X(n+τ)都具有相同的概率分布和統計特性，則H(X)和H(Xτ)的值接近于常數，根據互信息函數(1)式可推得

可見，H(X,Xτ)和 I(X,Xτ)呈近似相反的變化規律.互信息的極小值點即為聯合熵的極大值點在理論上得到驗證.

因此通過復雜的劃分網格或者進行網格標記求取互信息第一極小值點[6]從而確定相空間重構最佳延遲時間可以轉換為求取聯合熵H(X,Xτ)的第一極大值點.聯合熵的計算公式[9]可以表示為

由此可見，求取不同延遲時間下的聯合熵，找出聯合熵的第一極大值點所對應的τ，即為所求的最佳延遲時間點.

3 符號分析法求取極大聯合熵

符號分析法實際上是時間序列的符號化，該方法是通過在幾個可能值上將其時間序列離散化，從而將千變萬化的數據序列轉換為幾個數值或特殊符號的符號序列，該過程稱為粗粒化過程，這一過程能夠從動力系統中有效快速地捕獲有用定量信息，并且能夠降低噪聲的影響.將混沌時間序列通過粗粒化方法轉化為符號序列[10-14]，則其軌道演化的信息就通過符號序列達到了編碼.

時間序列符號化有二進制符號化規則、角區間符號化規則和概率統計符號化規則等，二進制劃分[13,15]是最簡單的一種劃分規則，只需給定一個閾值P0，時間序列中大于此閾值P0的取1，否則取0.閾值P0的選取有均值，零值等.則時間序列X(n)最終被轉換成符號序列{S(n)}，所得符號序列表征了兩種數據元模式，即

如圖1所示.

圖1 二進制符號化規則

二進制分割雖然簡便，但是由于其劃分比較粗糙，容易導致原始信息的遺失.為了解決這個問題，本文通過對相空間的分割從而使時間序列X(n)實現粗粒化過程[10-14].以符號數取d為例，劃分如下：

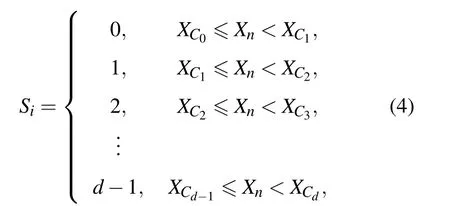
其中Xn為時間序列X(n)在n時刻的幅值大小，n=1,2,···,N.XC0,XC1,···,XCd為閾值即臨界點，Si為符號序列的符號集，并用相應的整數 i來代替，i=0,1,···,d-1. 則時間序列{X(1),X(2),X(3),···,X(N)} 可以轉換成整數集序列 {S(1),S(2),S(3),···,S(N)}.

時間序列被轉化成長整數集序列{S(1),S(2),···,S(N)} 后，要提取有用信息，需選擇標準分割長度L.將長整數集序列分割成長度為L的短序列，L個連續符號被編碼為十進制數，形成了新的整數集序列表示短序列從長整數集序列Si的第k個元素S(k)開始[10].

按照上式進行標記和辨識[10-12]，則離散的符號替代連續數據的原始時間序列，如圖2所示.

圖2 符號化時間序列圖

符號數d的個數可以通過使符號熵最大化來尋找[11,12]，為了方便起見，將混沌序列的臨界點(d+1)的個數置為11，即d=10.且分割長度L取2.

對時間序列X(n)及其延遲時間序列X(n+τ)，n=1,2,···,N，根據上面所介紹的粗粒化符號方法將其編碼成能捕獲用定量信息的特殊的十進制數序列Lx(n)和Lxτ(n)，則各個特殊十進制數出現的頻率為時間序列分析的指標，即為聯合概率P(Lx,Lxτ)，則符號分析法求取的聯合熵[16](3)式可以改寫為

4 數值仿真試驗

為了驗證該方法求取最佳延遲時間的準確性和優越性，我們分別對Lorenz，Rossler和Duf fing三種常見的混沌時間序列求取最佳延遲時間并畫出其吸引子的重構.

Lorenz系統的數值仿真實驗如圖3所示，Lorenz系統[17]方程

圖3 Lorenz系統(σ=16，b=4，r=45.92)的數值仿真實驗 (a)本文方法和互信息函數法求取最佳延遲時間的對比圖;(b)Lorenz吸引子在x-y平面上的投影圖;(c)τ=11時的Lorenz的重構吸引子圖

其中取 σ=16，b=4，r=45.92，此系統為混沌系統，用Runge-Kutta法求解方程(6)，步長h=0.01，取變量x為研究對象，去除前8000個點，得到一個7000個點的時間序列.通過符號分析法求取聯合熵H(Lx,Lxτ)的極大值點和通過網格劃分求取互信息I(X,Xτ)的極小值點的對比圖形如圖3(a)所示，從圖 3(a)可以看出，H(Lx,Lxτ)和 I(X,Xτ)的變化規律近似相反，并且都是在τ=11時取得第一個所對應的極值點，故可得由聯合熵第一極大值點法求得的相空間重構最佳延遲時間達到了與互信息法相同的效果;試驗過程中也大大地簡化了其計算量.圖3(b)是Lorenz吸引子在x-y平面的投影圖;圖3(c)是τ=11時的重構吸引子圖.從圖中可以看出τ=11時重構圖能夠很好的反映出Lorenz系統的雙圈拓撲結構.從而驗證了符號分析法求取極大聯合熵進而確定最佳延遲時間的有效性和優越性.

Rossler系統的數值仿真實驗如圖4所示，Rossler系統[18]方程

其中取 d=0.2，e=0.2，f=0.5，此時 Rossler系統為混沌系統，用Runge-Kutta法求解方程(7)，步長h=0.05，取變量x為研究對象，去除前50000個點，得到一個8000個點的時間序列.圖4(a)是Rossler系統處于混沌狀態時的聯合熵H(Lx,Lxτ)和互信息I(X,Xτ)的變化規律圖，兩者的變化成近似相反的規律，并且在互信息取得極小值點處，聯合熵處于極大值點，即τ=23;圖4(b)是Rossler吸引子在x-y平面的投影圖;圖4(c)是τ=23時的重構吸引子圖.比較重構前后吸引子在x-y平面投影，發現重構吸引子很好地保持Rossler吸引子的單圈結構.從而證明了符號分析法求取聯合熵極大值點即為最佳延遲時間的可行性.

圖4 Rossler系統(d=0.2，e=0.2，f=0.5)的數值仿真實驗 (a)本文方法和互信息函數法求取最佳延遲時間的對比圖;(b)Rossler吸引子在x-y平面上的投影圖;(c)τ=23時的Rossler的重構吸引子圖

Duf fing系統的數值仿真實驗如圖5所示，Duffing系統[1]方程

其中取 σ=0.06，a=0.7，F=7.5，此時 Duf fing 系統為混沌系統，用Runge-Kutta法求解方程(8)，步長h=0.05，取變量x為研究對象，舍去開始暫態點，得到一個7000個點的時間序列.從圖5(a)中能夠明顯看出Duf fing系統此時的聯合熵H(Lx,Lxτ)和互信息I(X,Xτ)的近似相反的變化規律，且由符號分析法求得的聯合熵H(Lx,Lxτ)的極大值點為τ=11，與互信息函數法得到的最佳延遲時間τ相同.圖5(b)是Duf fing吸引子在x-y平面的投影圖;圖5(c)是τ=11時的重構吸引子圖.比較重構前后吸引子在x-y平面投影發現重構效果良好.

圖5 Duf fing系統(σ=0.06，a=0.7，F=7.5)的數值仿真實驗 (a)本文方法和互信息函數法求取最佳延遲時間的對比圖;(b)Duf fing吸引子在x-y平面上的投影圖;(c)τ=11時的Duf fing系統的重構吸引子圖

5 結論

采用符號分析與極大聯合熵結合求取相空間重構的最佳延遲時間，不僅避免了計算互信息時的復雜的網格標記，而且無需計算X(n)和X(n+τ)的各自的概率分布及信息熵.該方法能達到與互信息方法計算最佳延遲時間同樣的效果，而且極大地簡化了計算，是求取最佳延遲時間的改進算法.理論分析與仿真實驗證明，該方法物理意義明顯，實際效果較好，能夠更多地保留原系統的動力學特征.

[1]JiangWL，ZhangSQ，WangYQ2005ChaosandWaveletBasedFault Information Diagnosis(Beijing：National Defence Industry Press)p46(in Chinese)[姜萬錄，張淑清，王益群2005基于混沌和小波的故障信息診斷(北京：國防工業出版社)第46頁]

[2]Fraser A M，Swinney H L 1986 Phys.Rev.A 33 1134

[3]Zhang S Q，Zhao Y C，Jia J，Zhang L G，Shangguan H L 2010 Chin.Phys.B 19 060514

[4]Tian Y C 1997 Systems Engineering Theory and Practice 05 48(in Chinese)[田玉楚1997系統工程理論與實踐05 48]

[5]Lu X Q，Cao B，Zeng M 2006 Chinese J.Comput Phys.23 184

[6]Zhang J，Fan Y Y，Li H M，Sun H Y，Jia M 2011 Chinese J.Comput Phys.28 469(in Chinese)[張菁，樊養余，李慧敏，孫恒義，賈蒙2011計算物理28 469]

[7]Xiao F H，Yan G R，Han Y H 2005 Acta Phys.Sin.54 0550(in Chinese)[肖方紅，閻桂榮，韓宇航2005物理學報54 0550]

[8]Zhang S Q，Jia J，Gao M，Han X 2010 Acta Phys.Sin.59 1576(in Chinese)[張淑清，賈健，高敏，韓敘2010物理學報59 1576]

[9]Zhu X K，Jia Y H 2005 Journal of Geomatics 05 3(in Chinese)[祝曉坤，賈永紅2005測繪信息與工程05 3]

[10]Xiao F H，Yan G R，Han Y H 2004 Acta Phys.Sin.53 2877(in Chinese)[肖方紅，閻桂榮，韓宇航2004物理學報53 2877]

[11]Lehrman M，Rechester A B 1997 Phys.Rev.Lett.78 54

[12]Rechester A B and White R B 1991 Phys.Lett.A 158 51

[13]Zhang Y 2004 J.Xiangtan Min.Inst.19 75(in Chinese)[張雨 2004湘潭礦業學院學報19 75]

[14]Azad R K，Rao J S，Ramaswamy R 2002 Chao Solitons and Fractals 14 633

[15]Xiang K，Jiang J P 2007 PR&AI 20 154(in Chinese)[向馗，蔣靜坪2007模式識別與人工智能20 154]

[16]Shi Y S，Jiang Y，Song Y X 2011 Journal of Aerospace Power 26 670(in Chinese)[史永勝，姜穎，宋云雪2011航空動力學報26 670]

[17]Yu W B 2008 Calculate Experiment and Analysis on Chaos(Beijing：Science Press)p33(in Chinese)[于萬波2008混沌的計算實驗與分析(北京：科學出版社)第33頁]

[18]Liu Z H 2006 Fundamentals and Applications of Chaotic Dynamics(Beijing：Higher Education Press)p71(in Chinese)[劉宗華 2006 混沌動力學基礎及其應用(北京：高等教育出版社)第71頁]