AlC分子X4Σ-和B4Σ-電子態的光譜性質*

劉 慧 邢 偉 施德恒 孫金鋒 朱遵略

1)(信陽師范學院物理電子工程學院，信陽 464000)

2)(河南師范大學物理與信息工程學院，新鄉 453007)

(2012年12月6日收到;2013年1月31日收到修改稿)

1 引言

隨著量化理論和計算技術的進步，人們已能對金屬及其碳化物的光譜性質開展研究，大大提高了我們對金屬團簇的了解.元素Al和C在太空中含量豐富，由它們構成的雙原子分子AlC可能存在于恒星大氣或星際空間中[1].深入了解AlC分子的光譜信息，將有助于確定宇宙中AlC分子的含量與分布，幫助我們了解宇宙的起源與演化.AlC分子的光譜性質已引起了一些光譜學家的關注[2-8].

實驗方面，早在1990年，Knight等[2]觀測了AlC分子的電子自旋響應光譜.確定了AlC分子的自旋分裂和精細結構常數，標定了該分子基態對稱性為4Σ-.1993年，Thoma等[3]在固態氬中采用傅里葉變換熒光光譜分析方法，探測到AlC分子.同年，Brazier[4]利用發射光譜對氣相AlC分子的光譜性質進行了研究，獲得了X4Σ-和B4Σ-態的某些光譜常數及分子常數.

理論方面，率先對AlC分子開展研究的是Zaitsevskii等[5].1986年，Zaitsevskii等[5]用多參考組態相互作用方法結合有效核勢近似，使用價DZ+P STO基組，研究了BC和AlC分子的電子結構.他們計算了 AlC 分子 X4Σ-，2Π，2Δ 和2Σ-等電子態的勢能曲線、偶極矩函數及相應的光譜常數.1988年，Bauschlicher等[6]采用MRCI理論方法計算了AlC分子大量低電子態的勢能曲線，得到了Te，Re和ωe等光譜常數.計算中Al和C原子分別使用的基組為：(20s13p6d4f)/[5s4p2d1f]和 (13s8p6d4f)/[4s3p2d1f]ANO.1999年，Gutsev等[7]采用耦合簇CCSD(T)理論結合[14s9p4d3f/7s7p43f]/C和[17s12p5d4f/7s7p5d4f]/Al的原子軌道基，計算了AlC分子基態及兩個低激發態的Re，Be和ωe等光譜數據.2001年，Tzeli等[8]采用CASSCF，MRCI及MRCI+Q等理論方法結合相關一致基aug-cc-pVQZ計算了AlC分子31個電子態的勢能曲線.獲得了這些電子態的 Te，Re，ωe，ωexe和αe等光譜常數.

分析已有的文獻[2—8]發現，大多數理論研究集中在AlC分子的光譜常數上，對于分子的振動能級Gυ、慣性轉動常數Bυ等分子常數則未見報道.且已有的理論計算均未考慮核價相關及相對論效應對分子能量及光譜性質的影響，使得理論結果與實驗結果之間還有較大偏差.為了深刻理解AlC分子的性質，我們對該分子X4Σ-和B4Σ-態的光譜性質進行了研究.

本文采用Davidson修正[9,10]的內收縮多參考組態相互作用[11,12]方法(MRCI+Q)及Dunning等[13-17]的相關一致基 aug-cc-pVnZ(n=D，T，Q，5，6)于 0.16—1.65 nm 的核間距范圍內計算了AlC分子X4Σ-和B4Σ-態的勢能曲線.對勢能曲線進行了相對論修正及核價相關修正計算，同時利用總能量外推進行基組截斷誤差修正.通過求解核運動的徑向Schrdinger方程，獲得了無轉動AlC分子兩個電子態的全部振動態.通過對前16個振動能級的擬合，得到了這兩個電子態的光譜常數.另外，本文還進一步計算了與每一振動態相對應的慣性轉動常數等分子常數.

2 理論方法

本文中，AlC(X4Σ-，B4Σ-)分子的勢能曲線是在MOLPRO2010.1程序包[18]中計算的.我們選擇能夠準確描述分子相關能的MRCI方法來研究AlC分子的光譜性質.CASSCF計算為隨后的MRCI及MRCI+Q計算提供參考波函數.

MOLPRO只能使用Abelian點群.對于具有簡并對稱性的分子，如對稱性為C∞v的AlC分子，計算中必須用C2v群替代.C2v群對應的不可約表示是a1/b1/b2/a2.這4種類型的軌道參與計算.具體地，在計算中將8個分子軌道放入活化空間，這包括4個a1、2個b1及2個b2軌道.其中，把Al原子的3s3p殼層和C原子的2s2p殼層的電子放入活性軌道，構成價態空間.也就是說，AlC分子最外層的7個電子分布于8個軌道中.因此，活性空間表示為(7，8).其余的電子則放入6個閉殼層軌道中，分別是4個a1、1個b1和1個b2軌道.這樣，實際參與計算的分子軌道共14個，分別為8a1/3b1/3b2.

勢能曲線的計算使用的基組是Dunning等的相關一致基，aug-cc-pVnZ(n=D,T,Q,5,6).計算在0.16—-1.65 nm核間距范圍內進行.步長一般取為0.05 nm，只是在平衡位置附近，為充分展示勢能曲線的性質，計算步長才取為0.02 nm.

即使是AlC這樣的小分子，核價相關效應及相對論效應對分子能量的影響也是不能忽略的.為評價核價相關效應及相對論效應對分子能量及光譜常數的影響，本文針對X4Σ-和B4Σ-這兩個電子態，于MRCI/aug-cc-pV6Z(AV6Z)和MRCI+Q/AV6Z理論水平計算了分別包含核價相關修正、相對論修正及同時包含兩種修正的勢能曲線.這里，我們利用三階Douglas-KrollHamilton近似[19,20]結合cc-pV5Z-DK相對論收縮基進行相對論能量修正計算(記為DK).由核價相關及相應的凍結核近似的能量差作為核價相關修正結果(記為CV).計算使用的基組是aug-cc-pCVTZ.需要說明的是，核價相關效應計算中Al原子2s2p3s閉殼層和C原子1s2s閉殼層的14個電子參與運算，Al原子1s層電子被凍結.與價態范圍內的計算相同，兩種修正計算也是在0.16—1.65 nm核間距范圍內進行的.除平衡位置附近計算步長取為0.02 nm外，其余的計算步長均取為0.05 nm.

為了彌補基組截斷誤差，本文將相關能外推公式擴展到總能量外推[21]，

其中，ΔEtotal,∞是外推至完全基組極限的總能量.ΔEtotal,X和 ΔEtotal,X+1分別是由 aug-cc-pVXZ和aug-cc-pV(X+1)Z基組計算的總能量.這里，我們使用aug-cc-pV5Z(表示為AV5Z)和AV6Z基組計算的勢能值結合(1)式進行總能量外推，得到外推的勢能曲線(表示為56).將外推的分子總能量加上相對論修正及核價相關修正結果，得到了同時考慮兩種修正的外推勢能曲線(記為56+CV+DK).

3 結果與討論

3.1 基組的收斂行為

首先來討論基組的收斂行為.使用MRCI和MRCI+Q理論方法不同的基組[AVnZ(n=D,T,Q,5,6)]計算出的勢能曲線，求解徑向振轉Schrdinger方程、并通過進一步的數據擬合，獲得了 Te，Re，ωe，ωexe，ωeye，Be和αe等光譜常數.限于篇幅，僅以 X4Σ-態的 Re，ωe和ωexe及 B4Σ-態的Te，Re和ωe為例進行討論.為便于比較，將外推結果與最近的實驗結果[4]一并列入表1中.

從表1可以看出，對于X4Σ-態，無論是MRCI還是MRCI+Q方法，隨著基組由aug-cc-pVDZ增大到AV6Z，Re，ωe及ωexe均向完全基組極限處收斂.其中，Re值逐漸縮短，ωe逐漸增大.與實驗結果[4]相比，隨著基組增大，Re和ωe向實驗結果靠攏.當外推至完全基組極限時，Re和ωe與實驗結果最接近.

對于B4Σ-態，在MRCI和MRCI+Q理論水平，隨著基組增大，Te，Re及ωe值均向完全基組極限收斂.可以看出，Re及ωe值隨基組變化的趨勢與X4Σ-態相同.其中，Re值逐漸縮短，ωe逐漸增大.與實驗結果[4]相比，隨著基組增大，ωe值逐漸向其靠攏.使用AV6Z基組計算的ωe值與實驗值仍有4.42 cm-1(MRCI)和6.54 cm-1(MRCI+Q)的偏離.當外推至完全基組極限時，與AV6Z計算的結果相比，ωe相對于實驗值的誤差分別減小了1.54 cm-1(MRCI)和1.64 cm-1(MRCI+Q)，使得ωe的計算精度顯著改善.容易看出，Te隨基組增大不斷降低.且隨著基組增大，Te明顯偏離實驗結果.分析表明，其原因在于核價相關效應和相對論效應對分子總能量產生或多或少的影響，特別是核價相關效應對小分子的總能量有較大影響.而上述計算均是在價態范圍內進行的，未考慮兩種效應對分子能量的影響，這應該是導致Te明顯偏離實驗值的原因.

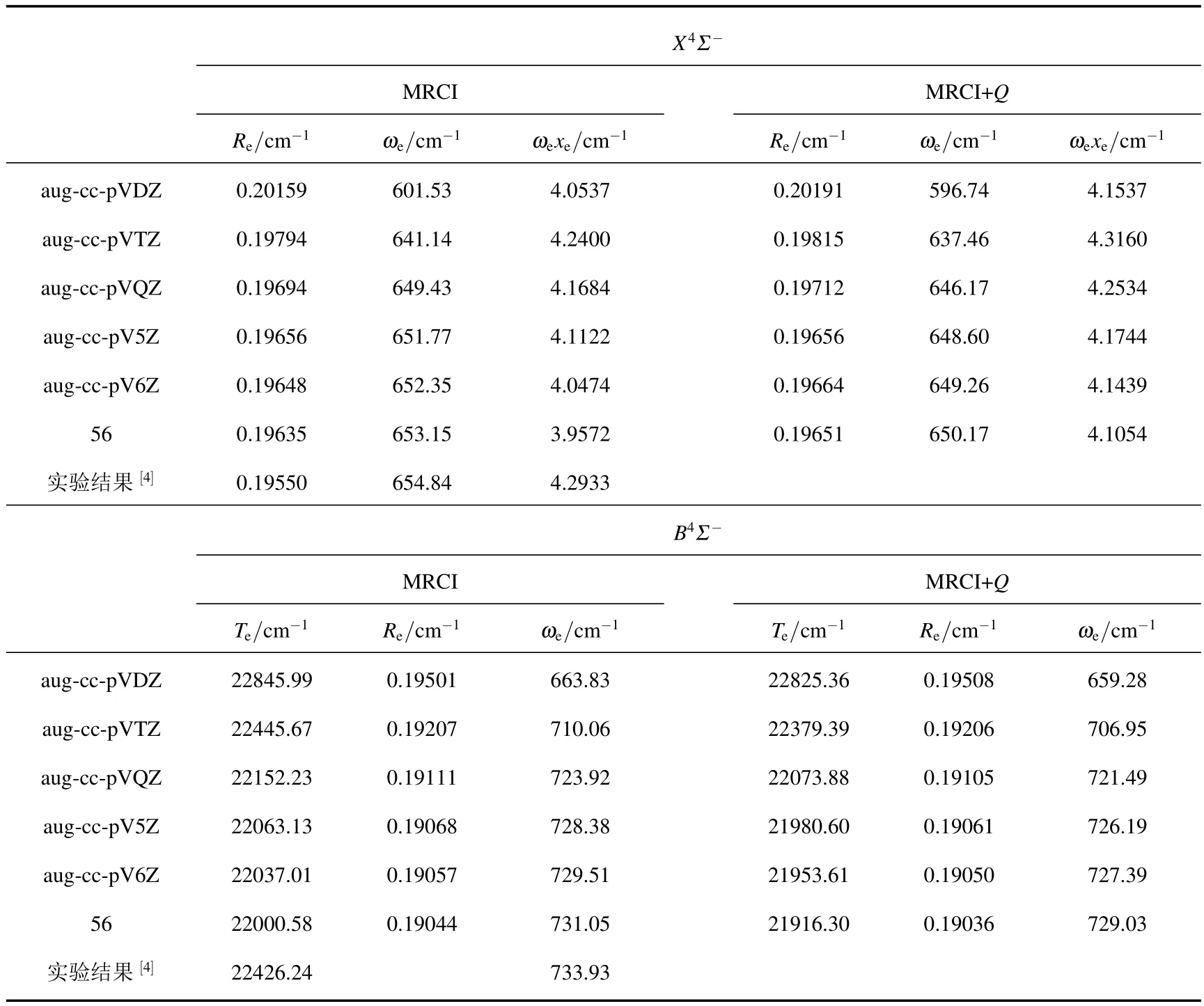
表1 MRCI和MRCI+Q理論方法下基組對X4Σ-態的Re，ωe及ωexe和B4Σ-態的Te，Re及ωe的影響

根據上述分析發現，經過總能量外推的勢能曲線擬合出的Re和ωe接近實驗值.可見，計算中使用大基組外推至完全基組極限可以明顯改善分子的Re和ωe，使分子光譜的預測更加準確.

3.2 核價相關及相對論修正對分子能量的影響

這里，以B4Σ-態為例，分析核價相關修正、相對論修正及Davidson修正對分子能量的影響.在平衡位置附近，核價相關修正使分子的總能量降低約0.00155(MRCI)/0.00262(MRCI+Q)Hartree(1 Hartree=27.21 eV).相對論修正給分子的總能量帶來約0.00068(MRCI)/0.00068(MRCI+Q)Hartree的降低.Davidson修正也使分子的能量發生一定的變化，使平衡位置的能量降低約0.00038 Hartree.可見，核價相關、相對論修正及Davidson修正對總能量產生了不同程度的影響.其中，核價相關修正的影響最大.

對MRCI/AV6Z及MRCI+Q/AV6Z理論水平下的勢能曲線進行相對論修正或/和核價相關修正.擬合這些勢能曲線，計算得到了各種修正下的光譜常數.將同時考慮相對論修正和核價相關修正的外推勢能曲線擬合，也獲得了包含兩種修正的外推光譜常數.限于篇幅，表2只列出了B4Σ-態的光譜常數Te，Re及ωe的CV，DK及CV+DK的修正量.為便于比較，實驗結果[4]也列入該表中.

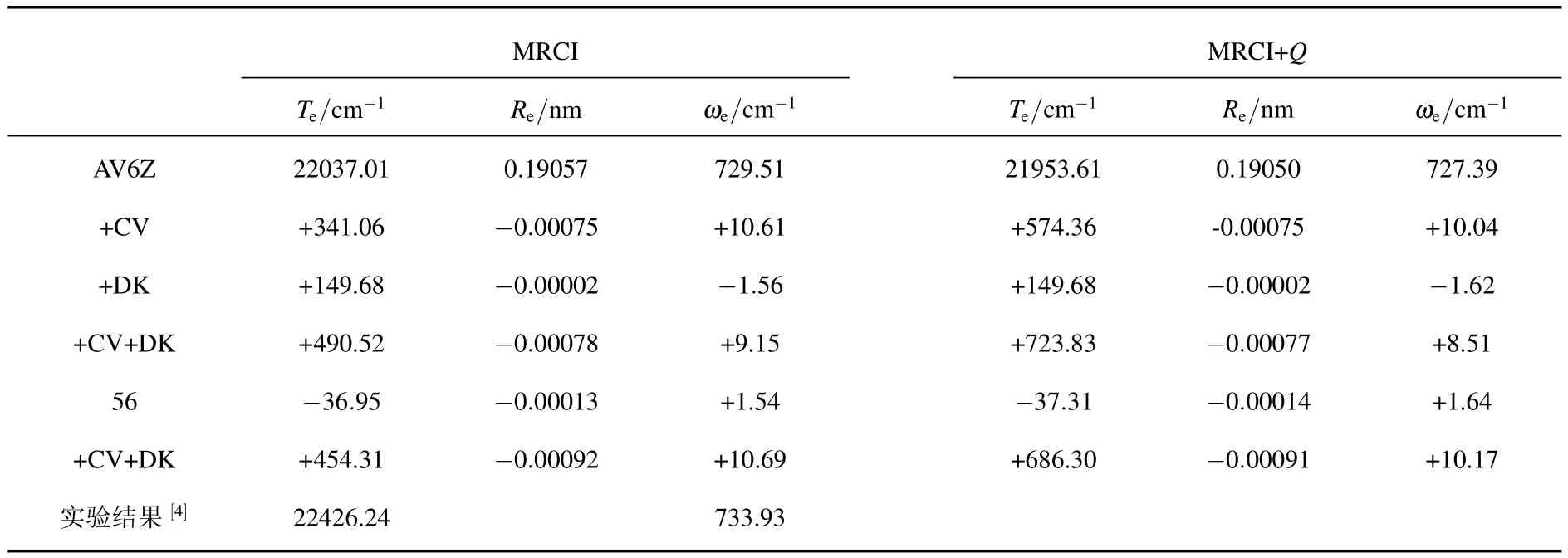
表2 各種修正對B4Σ-態的光譜常數Te，Re及ωe的影響

與實驗結果[4]比較發現，無論是采用MRCI方法還是MRCI+Q方法，核價相關修正使Re縮短0.00075 nm，使ωe增加約10 cm-1.考慮核價相關修正使Te的計算質量顯著提高.使Te分別升高341.06 cm-1/MRCI和574.36 cm-1/MRCI+Q.這些變化使Re，ωe和Te均向實驗結果靠攏.相對論修正對Re的影響很小，兩種理論方法下，僅使Re縮短約0.00002 nm.與核價相關修正產生的趨勢相反，相對論修正使ωe值分別減小1.56 cm-1(MRCI)和1.62 cm-1(MRCI+Q).兩種理論方法下，相對論修正均使Te增大149.68 cm-1.由表1可以清楚的看到，同時加入核價相關和相對論修正后，Re，ωe和Te均趨近于實驗結果.核價相關修正及相對論修正明顯改善了B4Σ-態光譜質量.

同時加入核價相關和相對論修正后，經總能量外推的ωe和Te與實驗值[4]符合很好.例如，MRCI+Q理論計算得到的ωe和Te偏離實驗值[4]分別只有0.49%和0.95%.根據誤差范圍分析方法[22,23]可以推斷，高于四重激發的能量校正很小，不超過74.30 cm-1，約占激發能的0.33%.

3.3 勢能曲線

根據上述討論及分析可以得出結論：使用大基組計算并將分子總能量外推至完全基組極限，同時考慮各種修正對分子能量的影響將有助于準確預測分子的勢能曲線及光譜性質.圖1展示了在MRCI+Q/56+DK+CV理論水平下獲得的X4Σ-和B4Σ-的勢能曲線.

圖1 MRCI+Q/56+CV+DK理論水平下的勢能曲線(1為X4Σ-：2 為 B4Σ-)

圖1顯示，X4Σ-和B4Σ-電子態的勢能曲線均光滑且收斂.基態有很深的勢阱，是一個穩定態;B4Σ-態是一個亞穩態，其勢能曲線分別存在一個勢阱和一個勢壘.勢壘大約位于0.2240 nm處，高約1215.89 cm-1(0.00554 Eh).

3.4 光譜常數

利用3.3中MRCI+Q/56+CV+DK理論水平下X4Σ-和B4Σ-態的勢能曲線，計算得到了這兩個態的光譜常數 Te，Re，ωe，ωexe，ωeye，Be和 αe.為便于比較，我們將這些數據和已有的實驗結果[4]及其他理論結果[5-8]一起列入表3中.

從表3可以清楚地看到，迄今為止只有4篇文獻[5—8]計算了X4Σ-態的光譜性質.具體地，Zaitsevskii等[5]用多參考組態相互作用方法結合有效核勢近似，計算了AlC分子基態的ωe和ωexe.其ωe和ωexe值與實驗值[4]分別相差25.84 cm-1(3.95%)和1.9067 cm-1(44.41%)，與實驗結果偏離較大.Bauschlicher等[6]采用CASSCF及MRCI理論方法并使用原子軌道基計算了該分子基態的Re和ωe.表3列出了在MRCI理論方法下得到的結果.其Re比實驗值長0.00231 nm(1.18%).ωe值與實驗值相差25.84 cm-1(3.95%).這些結果偏離實驗結果較大.Tzeli等[8]采用CASSCF，MRCI及MRCI+Q理論方法和aug-cc-pVQZ基組在價態范圍內計算了該分子基態的光譜常數.在MRCI方法下的結果見表3.由表3可以看出，其Re，ωe，ωexe和αe值與實驗值分別偏離0.82%，0.62%，1.71%和12.69%.Gutsev等[7]采用CCSD(T)方法和原子軌道基計算了該分子基態的Re，Be和ωe等光譜常數.它們與實驗結果符合較好，與本文的計算精度相當.然而，遺憾地是，他們的計算只涉及了有限的幾個光譜數據.

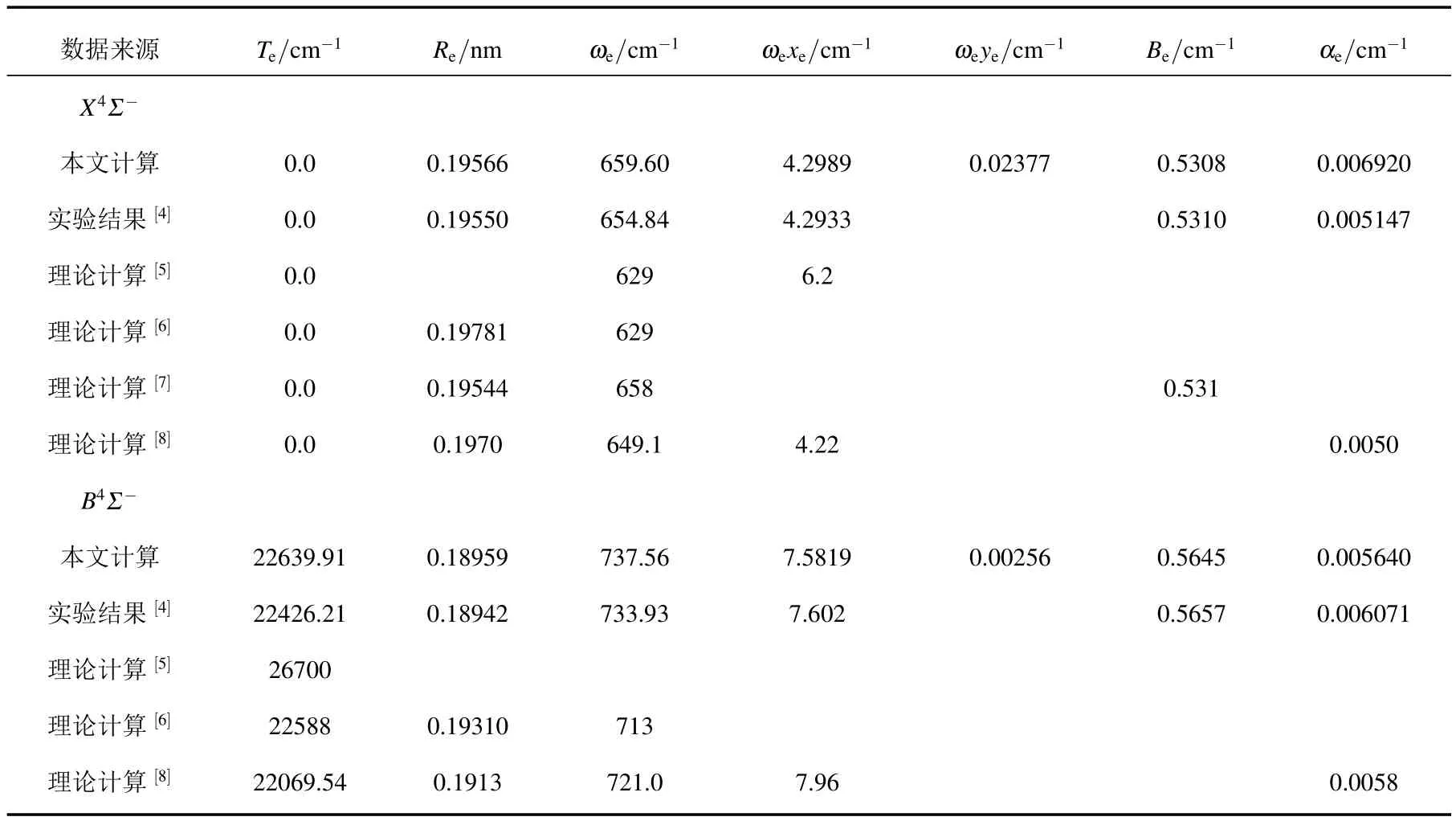
表3 AlC分子X4Σ-和B4Σ-電子態的光譜常數與實驗結果和其他理論計算的比較

對B4Σ-態，有3個研究小組[5,6,8]報道了其計算結果，這些結果均已列于表3中.由表3可知，Bauschlicher等[6]采用MRCI方法計算的Re和ωe分別偏離實驗值[4]1.94%和2.85%，只有Te和實驗值符合較好，偏離僅為0.72%.Zaitsevskii等[5]只計算了該態的激發能，且與實驗值相差4273.79 cm-1(19.06%)，偏離較遠.Tzeli等[8]的最好結果是在MRCI理論計算中獲得的，其Te，Re，ωe和ωexe值偏離實驗結果分別為1.59%，0.99%，1.76%和4.71%.

簡單的計算可知，本文在MRCI+Q/56+DK+CV理論水平下計算的光譜常數與實驗結果[4]符合較好.對于 X4Σ-態，本文的 Re，ωe，ωexe和 Be值與實驗值的偏離分別僅為0.08%，0.73%，0.13%和0.04%.對于 B4Σ-態，Te，Re，ωe，ωexe和 Be與實驗值的偏離分別僅為0.95%，0.09%，0.49%，0.26%和0.21%.只有小量αe與實驗值的偏離稍大.

通過上面的討論可知，本文在MRCI+Q/56+CV+DK理論水平下獲得的光譜數據整體上與實驗結果符合較好，優于已有的理論結果.可以確定，本文在MRCI+Q/56+CV+DK理論水平下得到的勢能曲線是準確、可靠的.

本文的計算結果之所以準確，其原因有多個方面.其一，本文在采用高精度的內收縮多參考方法的基礎上引入了核價相關修正及相對論修正，而其他的理論研究卻未將這些重要的影響因素包含在內.特別是，核價相關修正及相對論修正明顯改善了B4Σ-態的激發能.可見，即使是AlC這樣的小分子，要準確預測其光譜信息，核價相關效應及相對論效應的影響也必須考慮在內.其二，計算使用的總能量外推方法減小了由于基組截斷導致的殘余誤差.使得Re和ωe更加準確.再者，采用的Davidson修正也進一步減小了理論結果與實驗結果之間的偏離.

3.5 振動能級及慣性轉動常數

利用MRCI+Q/56+CV+DK理論水平得到的勢能曲線，通過求解核運動的徑向Schrdinger方程，找到了無轉動的X4Σ-和B4Σ-態的全部振動態，計算了與每一振動態相對應的振動能級和慣性轉動常數.只有前4個振動能級有實驗結果[4].這里，僅在表4中列出前10個振動態的計算結果.

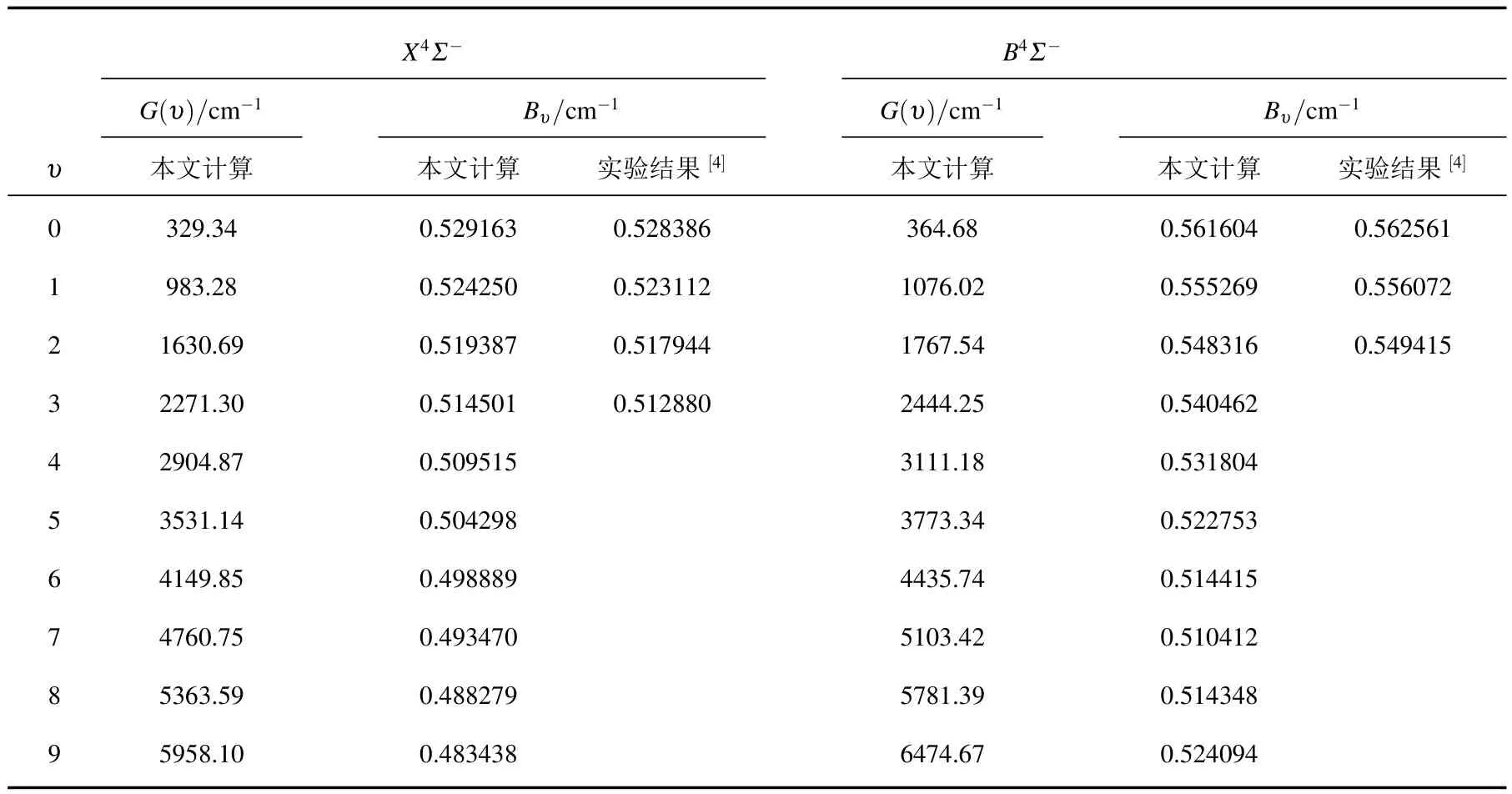
表4 AlC分子X4Σ-和B4Σ-電子態的分子常數與已有的實驗結果的比較

只有一篇文獻[4]報道了AlC分子X4Σ-和B4Σ-態的Bυ實驗值.為便于比較，我們將這些結果也列入表4中.從表中容易看出，本文計算獲得兩個電子態的Bυ與實驗結果符合很好.υ=0—3時，X4Σ-電子態的Bυ值與實驗值的相對誤差分別為0.15%，0.22%，0.28%和0.32%.B4Σ-態的Bυ值與實驗值的相對誤差分別為0.17%(υ=0)，0.14%(υ=1)和0.20%(υ=2).這些結果都是相當好的.

由于尚未找到AlC分子X4Σ-和B4Σ-態的振動能級和較高振動態的慣性轉動常數的實驗或理論結果，因而無法將本文得到的數據直接與其進行比較.但是，根據前文中關于這兩個電子態的光譜常數與實驗結果及其他理論計算的比較以及兩個電子態的分子常數與現有實驗結果的比較可以斷定，在MRCI+Q/56+CV+DK理論水平下得到的勢能曲線是準確的.盡管沒有更多的實驗數據供本文比較，我們依然有理由相信，AlC分子這兩個電子態的振動能級和較高振動態的慣性轉動常數的預測是可靠的.

隨著現代通信及微波毫米波技術的飛速發展，通信系統及射頻微波模塊逐漸向低成本、小型化，高性能的趨勢發展，這也是未來通信行業里極具競爭力的產品的特點。低溫共燒陶瓷(LTCC)技術由于成熟的發展理論，穩定的電氣性能和相對低廉的生產成本成為目前電子元器件小型化發展較為迅速的一個領域 [1-2]。LTCC是一種多層基板結構，它是以陶瓷材料作為介質基板，金、銀、銅等導電性能良好的金屬作為導電材料，將無源元件埋置于基板中，在800℃～900℃溫度下把陶瓷介質基板和導電金屬材料一同燒結成一種具有高性能、小型化的電子元件和電路組件。

4 結論

本文采用Davidson修正的MRCI方法及Dunning等的相關一致基于0.16—1.65 nm的核間距范圍內計算了AlC分子X4Σ-和B4Σ-態的勢能曲線.利用總能量外推公式對勢能曲線進行了外推.對分子能量進行了相對論修正及核價相關效應修正，獲得了同時考慮兩種效應修正的外推勢能曲線.擬合勢能曲線，得到了這兩個態的光譜常數Te，Re，ωe，ωexe，ωeye，Be和αe.詳細討論了基組及核價相關和相對論修正等對其能量和光譜常數的影響.在MRCI+Q/56+CV+DK理論水平下得到的光譜常數與已有的實驗結果符合較好.通過求解核運動的徑向Schrdinger方程，找到了AlC(X4Σ-，B4Σ-)分子的全部振動態.針對每一振動態，還分別計算了與其對應的振動能級和慣性轉動常數等分子常數.這些數據均與已有的實驗值一致.文中AlC(X4Σ-，B4Σ-)分子的振動能級和較高振動態的慣性轉動常數屬首次報道.本文的理論研究方法可以為同類研究提供有益的借鑒.本文的計算結果可為進一步的實驗研究提供參考.

[1]TsujiT 1973 Astron.Astrophys.23 411

[2]Knight L B，CobranchiS T，Herlong J O，Arrington C A 1990 J.Chem.Phys.92 5856

[3]Thoma A，Caspary N，WurfelB E，Bondybey V E 1993 J.Chem.Phys.98 8458

[4]Brazier C R 1993 J.Chem.Phys.98 2790

[5]ZaitsevskiiA V，Dement’ev A I，Zviadadze G N 1986 J.Less.Common Met.117 237

[6]Bauschlicher C W，Langhoff S R，Pettersson L G M 1988 J.Chem.Phys.89 5747

[7]Gutsev G L，Jena P，Bartlett R J 1999 J.Chem.Phys.110 2928

[9]Langhoff S R，Davidson E R 1974 Int.J.Quantum Chem.8 61

[10]Richartz A，Buenker R J，Peyerimhoff S D 1978 Chem.Phys.28 305

[11]Werner H-J，Knowles P J 1988 J.Chem.Phys.89 5803

[12]Knowles P J，Werner H J 1988 Chem.Phys.Lett.145 514

[13]Dunning T H 1989 J.Chem.Phys.90 1007

[14]Woon D E，Dunning T H 1993 J.Chem.Phys.98 1358

[15]Van Mourik T，Wilson A K，Dunning T H 1999 Mol.Phys.96 529

[16]Van Mourik T，Dunning T H 2000 Int.J.Quantum Chem.76 205

[17]De Jong W A，Harrison R J，Dixon D A 2001 J.Chem.Phys.114 48

[18]Werner H J，Knowles P J，Lindh R，Manby F R，Schtz M，CelaniP，Korona T，Mitrushenkov A，Rauhut G，Adler T B，Amos R D，Bernhardsson A，Berning A，Cooper D L，Deegan M J O，Dobbyn A J，Eckert F，GollE，HampelC，Hetzer G，Hrenar T，Knizia G，KpplC，Liu Y，Lloyd A W，Mata R A，May A J，McNicholas S J，Meyer W，Mura M E，Nicklass A，PalmieriP，P flger K，Pitzer R，Reiher M，Schumann U，StollH，Stone A J，TarroniR，Thorsteinsson T，Wang M，Wolf A MOLPRO(a package of ab initioprograms)(version 2008.1)http：//www.molpro.net

[19]Reiher M，Wolf A 2004 J.Chem.Phys.121 2037

[20]Wolf A，Reiher M，Hess B A 2002 J.Chem.Phys.117 9215

[21]Liu H，Xing W，ShiD H，Sun J F，Zhu Z L 2012 Acta Phys.Sin.61 203101(in Chinese)[劉慧，邢偉，施德恒，孫金峰，朱遵略2012物理學報61 203101]

[22]Bauschlicher C W，Partridge H 1996 Chem.Phys.Lett.257 601

[23]Karton A，Martin J M L 2006 J.Chem.Phys.125 144313