基于檢測數據更新的混凝土碳化深度預測

2013-03-05 07:24:54劉均利

土木與環境工程學報 2013年3期

劉均利，方志

（1.湖南大學土木工程學院，長沙410082；2.桂林理工大學廣西巖土力學與工程重點實驗室，廣西桂林541004）

在一般大氣環境中，混凝土碳化是導致鋼筋銹蝕的主要原因之一。混凝土碳化機理的研究已比較充分，但混凝土碳化受多種因素影響，如水泥品種和用量、水灰比、混凝土的養護、混凝土強度等級和環境因素等［1－2］。國內外學者從不同角度提出了許多混凝土碳化深度預測模型，牛荻濤等［1］以抗壓強度為主要參數，考慮澆筑面、角部位置、工作應力、環境溫度和濕度等因素影響，提出一個半理論半經驗隨機模型；張譽等［2］以水灰比和水泥用量為主要參數，并通過快速碳化試驗數據對模型進行了修正，建立了一個既有理論依據又有實用價值的碳化深度預測模型；Hakkinen［3］以抗壓強度為主要參數并考慮水泥摻合料和環境因素影響，建立一個模型，目前在歐洲廣泛應用；Wang等［4］建立了能考慮粉煤灰影響的預測混凝土碳化深度的數值模型；Talukdar等［5－6］以CO2濃度、CO2擴散系數為主要參數，建立了能考慮氣候影響的碳化深度預測模型。由于各個碳化深度預測模型考慮的側重點不同，對同一工程，不同模型的預測結果存在顯著的差異。盧峰等［7］通過不同預測模型計算結果與實際工程檢測數據對比，發現計算結果與實際工程測試結果差異普遍在30%～50%左右，且不同模型的適用條件也不同，如張譽模型計算粉煤灰混凝土碳化深度的精度較高，而牛荻濤模型計算普通水泥混凝土碳化深度的精度較高，模型的選擇對評估結果的精度影響顯著。

對一個既有結構，其各種因素對碳化的影響都已定型，理論上可依據碳化深度實測值確定碳化的概率模型，但碳化檢測是有損檢測，實際工程檢測中樣本數量受到限制而缺乏足夠的代表性，單依靠小樣本檢測數據進行碳化可靠性分析可能導致統計不確定性太大［8］，且當前工程檢測中常用測量碳化深度的酚酞指示劑測試法易受外界因素影響，精度不高。貝葉斯方法可以綜合數學預測模型的先驗信息和現場檢測的自然信息，更新預測模型，提高預測的精度。衛軍等［8］利用檢測數據對混凝土模型和鋼筋銹蝕模型的參數進行了更新，并利用更新后的參數計算結構的可靠度；Caspeele等［9］應用貝葉斯方法將文獻資料信息和少量試驗資料結合，提高混凝土抗壓強度的統計分布精度；Hyun等［10］應用貝葉斯方法將驗證荷載引入樁基的可靠性設計；吳本英等［11］采用貝葉斯理論結合模型信息和檢測信息，對碳化深度預測模型的參數進行更新，更新后的模型預測精度提高，同時發現如果模型選擇恰當，更新后結果與實際工程吻合良好，如果模型選擇不當，更新后的預測結果仍不理想。

筆者提出一個預測混凝土碳化深度的兩層次貝葉斯更新模型，將碳化預測模型的均值和方差均看做隨機變量，首先選擇幾個模型作為先驗模型并對其平均賦以權重，然后應用檢測信息，對模型的分布參數和模型權重進行更新，最后用更新后的模型參數和權重預測混凝土碳化深度。

1 雙層貝葉斯更新模型

1.1 預測模型分布參數的貝葉斯更新

已有研究成果證明，混凝土的碳化深度x較好地服從正態分布N（μ，σ2），由于存在主觀不確定性，預測模型中碳化深度x的均值μ和方差σ2均應為隨機變量，在對具體工程的碳化深度檢測前，對均值μ和方差σ2的認識來自經驗和已有研究成果（模型），這種認識叫做先驗信息［1，12－13］。

采用共軛分布確定碳化深度x的均值μ和方差σ2的先驗分布和后驗分布［14］，當σ2已知時，均值μ符合正態分布：

方差σ2服從倒伽馬分布：

均值μ和方差σ2的共軛先驗分布為：

式中：k0、υ0、σ0和μ0為超參數［14］，可根據先驗矩法、先驗分位數等方法確定。均值μ和方差σ2的先驗分布反映過去的研究成果對事物的認識，混凝土結構運營一段時間，通過檢測獲得一個碳化深度的樣本x1，x2，…，xn后，對均值μ和方差σ2有了新的認識。樣本x1，x2，…，xn的聯合密度函數可表示為：

均值μ和方差σ2的后驗分布為［14］：

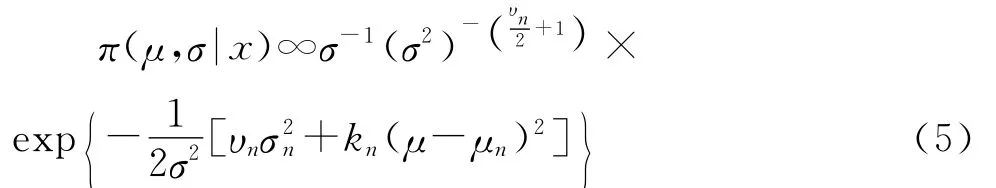
式中：

后驗分布與先驗分布形式上相同，只是以μn、υn、kn和υnσ代替μ0、υ0、k0和υ0σ。后驗均值μn是先驗均值μ0和檢測均值ˉx的加權平均值。k0的含義：先驗信息相當于“k0個樣本”所提供的信息，kn＝k0＋n相當于先驗信息和后驗信息的“總樣本容量”。后驗自由度υn是先驗自由度加樣本容量。

1.2 模型不定性的貝葉斯更新

假如有m個模型可以預測事件X的結果，但不知哪一個模型是最合理的，即m個模型都有可能是合理的，則事件X發生的概率可表示為：

式中：P（Mi）是模型的權重，滿足不知哪個模型最合理時，可取相同的概率，即P（Mi）＝P（Mj）。θi＝｛θi1，θi2，…，θin｝表示模型 Mi的分布參數向量；π（θi｜Mi）表示模型Mi中參數θi的先驗分布；P（X｜θi，Mi）是事件X 對（Mi，θi）的條件分布。

模型Mi與分布參數θi的先驗分布π（Hi）為：

當獲得了X的觀測數據x后，可根據貝葉斯原理給出Hi的后驗分布：

將式（12）兩邊對θi積分，可得Mi的后驗分布：

當有多個觀測值時，P（x｜Hi）即樣本x的聯合概率密度函數。式（12）除以式（13），可得θi的后驗分布：

則X的后驗分布可表示為

在沒有獲得檢測數據前，應用貝葉斯先驗模型式（10）預測碳化深度值；當獲得檢測數據后，應用貝葉斯后驗模型式（15）預測碳化深度值。隨著服役期增長，檢測數據增多，可以不斷對碳化深度預測模型進行貝葉斯更新，提高預測精度。

2 算例

張令茂［15］做了一個10a期的室內暴露碳化試驗，采用425＃普通水泥（含15%摻合料），室溫20℃，CO2的體積分數為340×106，相對濕度70%，其中10號試件摻加30%粉煤灰。檢測了0.5、1、2、5和10a的碳化深度資料，如表1所示。

表1 試驗數據

試驗結果和牛荻濤模型、張譽模型和Hakkinen模型的計算結果對比見圖1。對1號試件，牛荻濤模型與檢測結果最接近，誤差在30%左右，Hakkinen模型與試驗結果相差最大，誤差接近100%；對10號試件，Hakkinen模型吻合最好，誤差小于15%，牛荻濤模型誤差最大，超過100%。

圖1 碳化模型計算結果與試驗結果對比

取碳化系數為統計量，牛荻濤模型［1］是隨機模型，可計算標準差，張譽模型［2］和 Hakkinen［3］模型是確定型模型，取與牛荻濤模型相同的離散系數作為先驗信息。由于文獻［15］只給出了5次碳化深度實測值，假設實測是3個試件均值，總共測試15個試件，根據統計理論計算出1號試件和10號試件的實測均值和方差。

貝葉斯更新后的模型權重見表2。對1號試件，牛荻濤模型吻合最好，更新后牛荻濤模型權重最大，而Hakkinen的權重更新后接近0。而10號試件，Hakkinen模型吻合最好，更新后的權重也最高。碳化系數的密度曲線見圖2，先驗分布是3個模型的平均值，試驗數據曲線是5次檢測總樣本曲線。隨著更新次數增多，樣本量增大，模型計算的碳化系數中值逐步接近實測值，標準差也逐步接近真實標準差，當實驗樣本無限大時，貝葉斯更新的概率密度曲線與真實概率密度曲線重合。圖3為更新后碳化深度預測值，更新次數越多，結果越精確，更新后的預測結果精度高于單一模型預測精度。

表2 各種模型的先驗與后驗權重

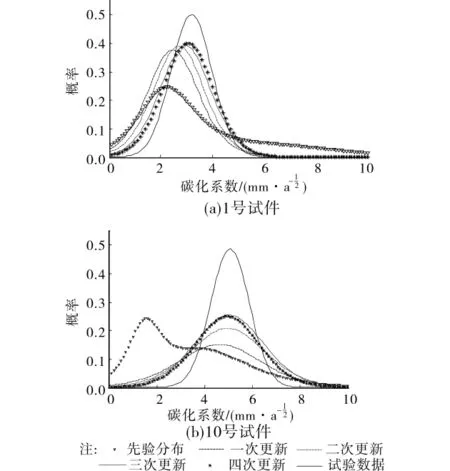
圖2 碳化系數的先驗與后驗分布

3 結語

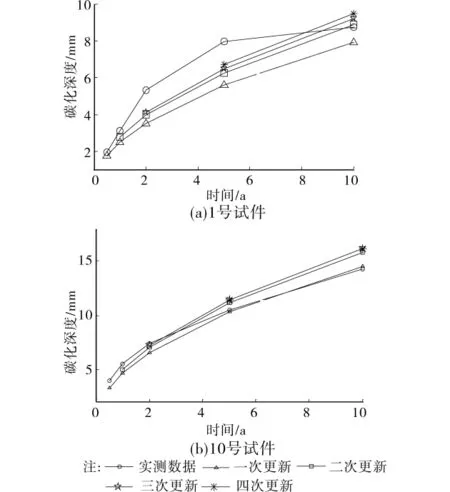
圖3 碳化深度均值的貝葉斯更新

通過貝葉斯方法，將小樣本工程檢測數據與現有碳化預測模型結合，對模型的選擇和模型參數的取值進行更新，有效降低模型選擇和模型參數的主觀不定性和隨機性。本方法尤其適用于存在多個結果差異較大的預測模型情形，采用本方法，僅應用少量檢測數據即可獲得更合理的結果，如在工程結構生命期內定期檢測，可實現貝葉斯動態信息更新，使預測結果更加接近工程結構的實際情況。

［1］牛荻濤，董振平，浦聿修.預測混凝土碳化深度的隨機模型［J］.工業建筑，1999，29（9）：41－44.Niu D T，Dong Z P，Pu Y X.Random model of predicting the carbonated concrete depth［J］.Industrial Architecture，1999，29（9）：41－44.

［2］張譽，蔣利學.基于碳化機理的混凝土碳化深度實用數學模型［J］.工業建筑，1998，28（1）：16－19.Zhang Y，Jiang L X.A practical mathematical model of concrete carbonation depth based on the mechanism［J］.Industrial Architecture，1998，28（1）：16－19.

［3］Hakkinen T.Influence of high slag cement on the basic mechanical properties and carbonation of concrete［M］.Espoo：Technical Research Centre of Finland，1993.

［4］Wang X Y，Lee H S.A model for predicting the carbonation depth of concrete containing low－calcium fly ash［J］.Construction and Building Materials，2009，23（2）：25－733.

［5］Talukdar S，Banthia N，Grace J R.Carbonation in concrete infrastructure in the context of global climate change－Part 1： Experimental results and model development ［J］.Cement and Concrete Composites，2012，34（8）：924－930.

［6］Talukdar S，Banthia N，Grace J R.Carbonation in concrete infrastructure in the context of global climate change：Part 2－Canadian urban simulations ［J］.Cement and Concrete Composites，2012，34（8）：931－935.

［7］盧峰，刁波.混凝土碳化及鋼筋銹蝕預測模型對比驗證［J］.混凝土，2009（1）：36－40.Lu F，Diao B.Contrast and verification of the concrete carbonation model and rebar corrosion model ［J］.Concrete，2009（1）：36－40.

［8］衛軍，羅扣.基于貝葉斯方法的時變可靠度分析［J］.華中科技大學學報：自然科學版，2007，35（2）：1－3.Wei J，Luo K.Analysis of time－dependent reliability by using Bayesian approach ［J］.Journal of Huazhong University of Science and Technology：Nature Science Edition，2007，35（2）：1－3.

［9］Caspeele R，Taerwe L.Bayesian assessment of the characteristic concrete compressive strength using combined vague－informative priors ［J］.Construction and Building Materials，2012，28（2）：342－350.

［10］Hyun P，Kim D，Kichung C.Implementation of bayesian theory on LRFD of axially loaded driven piles［J］.Computers and Geotechnics，2012，42（1）：73－80.

［11］吳本英，周錫武.基于貝葉斯方法的混凝土結構碳化深度預測研究［J］.武漢理工大學學報，2011，33（3）：103－107.Wu B Y，Zhou X W.Analysis of time－dependent reliability by using Bayesian approach ［J］.Journal of Wuhan University of Technology，2011，33（3）：103－107.

［12］Monteiro I，Branco A，Debrito J，et al.Statistical analysis of the carbonation coefficient in open air concrete structures ［J］.Construction and Building Materials，2012，29（2）：263－269.

［13］貢金鑫，水金鋒，趙尚傳.基于碳化的既有鋼筋混凝土橋梁耐久性的概率分析［J］.混凝土，2006（1）：18－22.Gong J X，Shui J F，Zhao S C.Probability analysis for existing reinforced concrete bridges durability regarding carbonation［J］.Concrete，2006（1）：18－22.

［14］Zhang R X，Mahadevan S.Model uncertainty and Bayesian updating in reliability－based inspection ［J］.Structural Safety，2000，22（2）：145－160.