回轉曲面的可展切曲面

毛 昕， 楊靜林， 馬明旭

（東北大學機械工程與自動化學院，遼寧 沈陽 110004）

回轉曲面的可展切曲面

毛 昕， 楊靜林， 馬明旭

（東北大學機械工程與自動化學院，遼寧 沈陽 110004）

論文系統地提出了構造回轉曲面的可展切曲面及它們間映射分析的理論與方法，建立了回轉曲面可展切柱面和可展切錐面的數學模型以及曲面間的映射關系。根據回轉曲面及其可展切曲面間微分長度比的理論分析，推出了映射中極值映射曲線和等距映射曲線的微分方程，通過整體和局部的變形分析，可以準確地掌握回轉曲面與其可展切曲面間映射中的變形情況。

幾何計算；回轉曲面；可展切曲面；映射分析

工程應用中，可展曲面的構造和分析近年來得到越來越廣泛的關注和研究[1-4]。作者在前面的研究中，提出了曲面片的可展切曲面及其映射分析的理論和方法。對于曲面片Σ：r ( u, v)，沿其上任意曲線 Γ:r=r( u( t), v( t) ) =r( t)，存在一可展曲面 Σ1：r1( t, w) 沿曲線Γ與Σ相切，把 Σ1稱為Σ的可展切曲面[5-6]，其表達形式為

式中 l( t)為 Σ1特征線（直素線）方向的單位矢量，n( t )為Γ曲線上參數t處曲面的單位法矢。可展切曲面及其映射分析的理論和方法可以在曲面結構設計、不可展曲面近似展開及誤差分析和紋理映射及變形控制等方面得到應用[7]。在實際生產中，回轉曲面有著非常廣泛的應用，因此，本文在已有研究的基礎上著重討論回轉曲面的可展切曲面，建立構造回轉曲面的可展切曲面及其它們間映射分析的理論模型，并給出在近似展開及其變形分析中的應用實例。

1 回轉曲面的可展切曲面

設回轉曲面由 xoz坐標面上的曲線C:x=f( v), z=g( v)繞z軸旋轉而成，曲面的參數方程為rv={f′( v ) cosu,f′( v) sinu, g′( v)}，可得曲面上任意點處的單位法矢（當 f( v)≥ 0時，取上面符號；當 f( v) ＜ 0時，取下面符號）

1.1 Γ曲線為經線時的可展切曲面

此時對于Γ曲線有：u=u0, v = t ，將其分別代入式（1）和式（2）得Γ曲線的方程

和Γ曲線上曲面的單位法矢

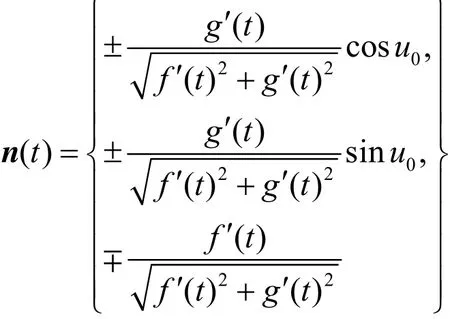
切曲面特征線方向的單位矢量

式中，當 f′( v ) g ′( v ) -f′(v ) g ′( v )≥ 0時，取上面符號，否則取下面符號。由式（4）可見 l( t)為常矢量，說明可展切曲面 Σ1沿 r( t)的各條直素線互相平行， Σ1一般為柱面。其方程為

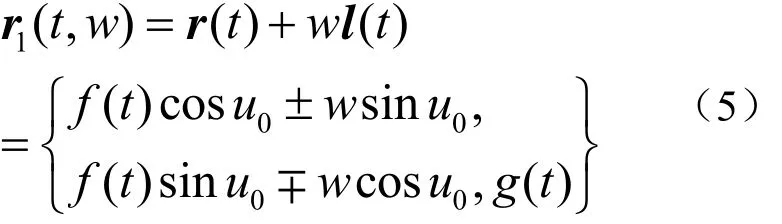
1.2 Γ曲線為緯線時的可展切曲面

此時對于Γ曲線有：u=t, v=v0，將其分別代入式（1）和式（2）得Γ曲線的方程

和Γ曲線上曲面的單位法矢

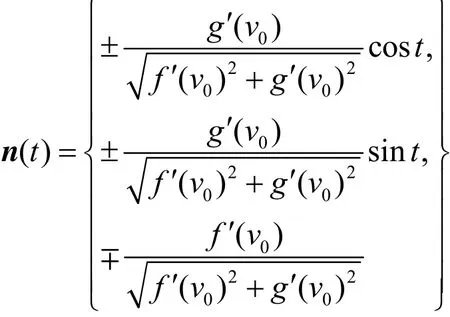
切曲面特征線方向的單位矢量

由于特征線經過緯線Γ，且由式（7）可見，l(t)在z軸上的分量為常數，說明 l( t)與z軸有不變的夾角，所以 Σ1為圓錐面。其方程為

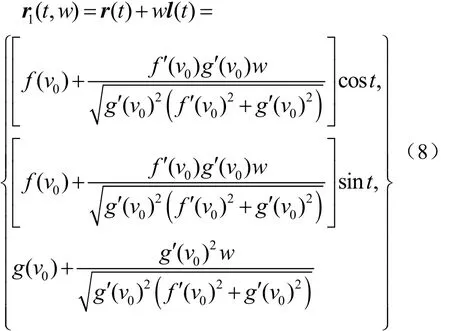
由上式可解得圓錐錐頂的坐標為

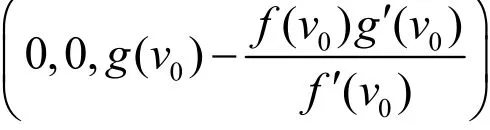
2 映射分析中的微分長度比

在映射分析中，首先建立回轉曲面與其可展切曲面間的映射關系，之后通過整體映射關系分析兩曲面間參數曲線長度的相對變化、對應區域面積的相對變化和對應參數曲線交角的相對變化；再通過局部映射關系分析對應點處各方向上的微分長度比，并進而獲得曲面映射中的最大、最小長度相對變化曲線（極值映射曲線）和長度不變的曲線（等距映射曲線）。

2.1 回轉曲面的微分長度比

微分長度比定義為對應點處沿某方向微分長度（弧素）的比值，即：

微分長度比

式中，ds和ds1分別為曲面∑ 和∑1在對應點處的微分弧長，E、F、G和E1、F1、G1分別為兩曲面的第一基本量，由上式可見，長度比是曲面上點(u ,v)和切方向(dv/du)的函數。

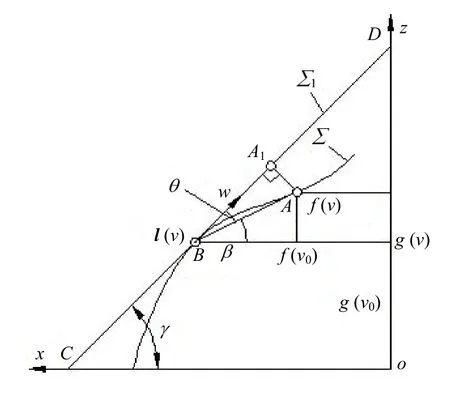
對于回轉曲面，微分長度比可以用方向角β來表示。圖1中的ABCD為曲面在點A(,)u v處的微分單元，β為點A處的切方向(d/dv u)與緯線切向的夾角。容易看出：

圖1 回轉曲面的微分單元

將式（10）和回轉曲面的第一基本量E=f2(v), F=0,G=f′2(v) + g ′2(v)代入公式（9）并整理有：

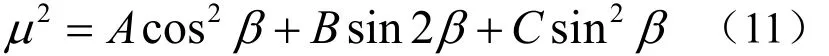
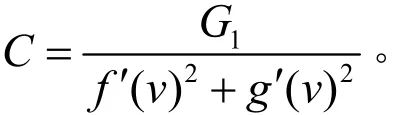
2.2 特殊方向的微分長度比

2.2.1 微分長度比取極值的方向

在式（11）中，把2μ對β求偏導并令其等于零，有=(C - A) sin2β+ 2B cos2β=0

代入式（10）并整理，有

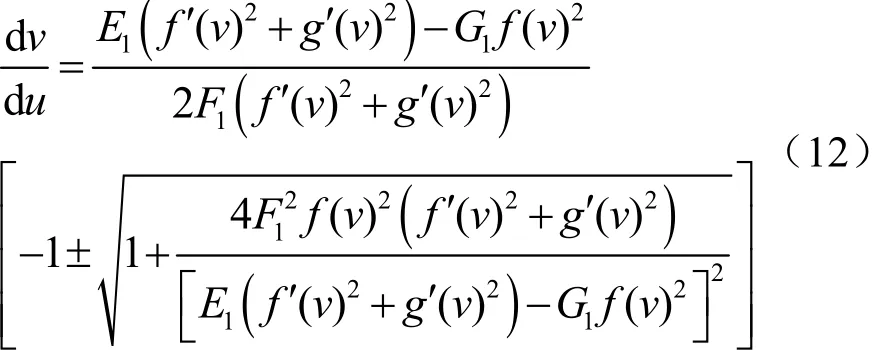
上式即為極值映射曲線的微分方程式，兩個解分別對應映射中變形最大和最小的兩族曲線，曲線上任一點的切矢方向是該點處微分長度比取極值的方向。

2.2.2 微分長度比等于1的方向

在該方向上兩曲面的微分長度相同，沒有長度變化。令式（11）等于1，即

μ2=A cos2β+ Bsin2β + C sin2β=1可解得

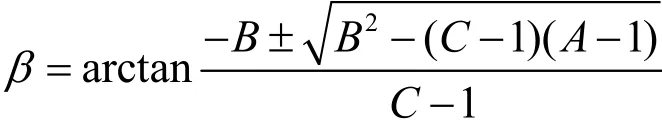
將其代入式（10）并整理，有

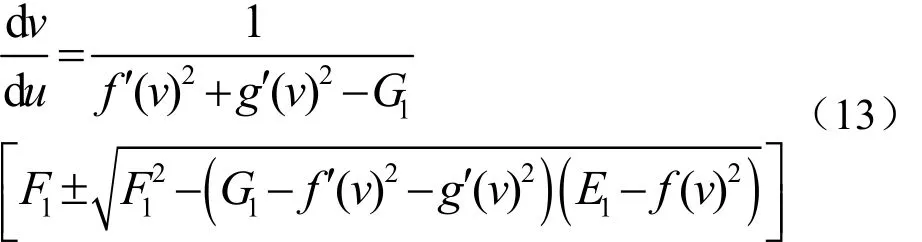
上式即為等距映射曲線的微分方程式，兩個解分別對應曲面映射中長度沒有發生變化的兩族曲線，該曲線上任意點的切矢方向是該點處微分長度比等于1的方向。

3 回轉曲面與其可展切曲面間的映射

3.1 回轉曲面與其可展切柱面間的映射

這時Γ曲線為回轉曲面的經線，切曲面為柱面。如圖2所示，回轉曲面Σ中的點A映射為切柱面 Σ1中同緯度直素線上的點 A1，取Γ曲線的u 向參數為 U，并 取參數變換 t =v, w =f (v)tan(u- U)，將其代入式（5），便得到以 u, v為參數的 Σ1的方程

圖2 切柱面的映射關系

由式（14）可得切柱面 Σ1的第一基本量

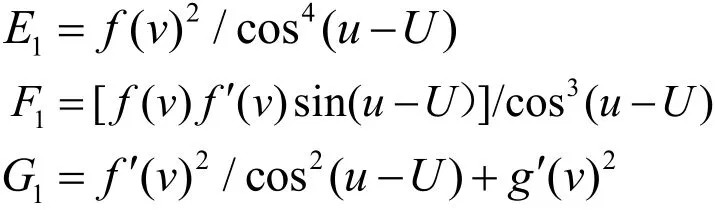
將其代入式（12），得到極值映射曲線的微分方程

式中：

再將切柱面 Σ1的第一基本量代入式（13），便得到等距映射曲線的微分方程

3.2 回轉曲面與其可展切錐面間的映射

這時Γ曲線為回轉曲面的緯線，切曲面為圓錐面。如圖3所示，回轉曲面Σ中的點A映射為切錐面 Σ1中同經度直素線上的點 A1，其中AA1⊥ CD。取變換

并將其代入式（8），便得到 u, v為參數的 Σ1方程：

式中：

由式（17）可得切錐面的第一基本量：E1=(f( v0) + ab( v ))2， F1=0，，由于 F1=0，根據極值映射曲線的微分方程式（12）可知，若d v=0,v=常數，即u曲線；若d u=0,u=常數，即v曲線。兩族參數曲線即為映射中的極值映射曲線。

再將切錐面的第一基本量代入式（13），便得到等距變換曲線的微分方程

4 可展切曲面在環面片近似展開中的應用

下面以環面片為例說明回轉曲面的可展切曲面在近似展開及其變形分析中的應用，這里把環面片用其可展切柱面進行替代來近似展開。

對于圓環面有：f( v) =R + r cosv，g( v)=r sinv，由式（1）可得圓環面的方程r(u, v)={(R+rcosv) cosu,( R + rc osv) sinu, rs in v}由式（14）得其切柱面的方程

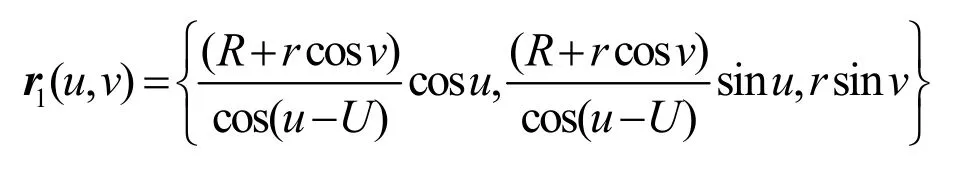
環面的第一基本量：E=(R + r cosv)2，F=0，G=r2。

切柱面的第一基本量：

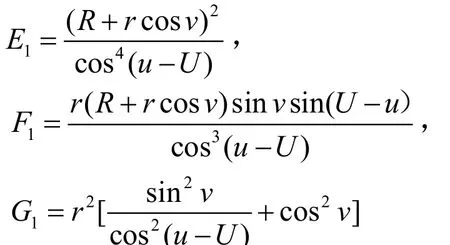
環面片取邊界條件 [u1, u2]=[0°, 20°] ,[v1, v2]=[30°, 150°],Γ 曲線的 u 向參數U=10°。環面的半徑 R=40，母線圓半徑r=20。

4.1 環面片的展開

把切柱面映射到平面上，得到展開圖的方程：

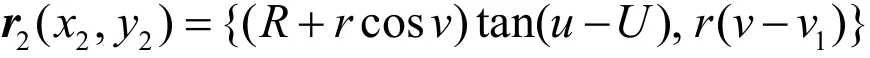
代入邊界條件后的展開圖如圖4所示。

圖4 環面片的展開圖

4.2 變形分析

4.2.1 整體變形分析

通過環面和其切柱面的第一基本量，分別計算它們的經線長度、緯線長度、曲面片面積和參數曲線交角，進而得出相對經線長度變化 δLv、相對緯線長度變化 δLu、相對面積變化 δS 和相對參數曲線交角變化 δA 。圖 5 是當u1=0,U=u2/2 時緯線長度和面積的相對變化情況，它們具有相同的變化值，并隨參數 u2的增大快速增加。由圖6可見，當u=U時，經線長度變化為零，兩曲面沿該經線相切；經度離此越遠，經線長度的相對變化也越大。圖7為參數曲線交角的相對變化曲線，當u=U時，交角的相對變化為零；當參數v固定時，隨參數u的減小， δA 約呈線性趨勢增加；在參數u=U的兩端，δ A 為對稱分布，即有 δA ( u, v0)=δA ( u2-u, v0)。

圖5 緯線長度和面積相對變化

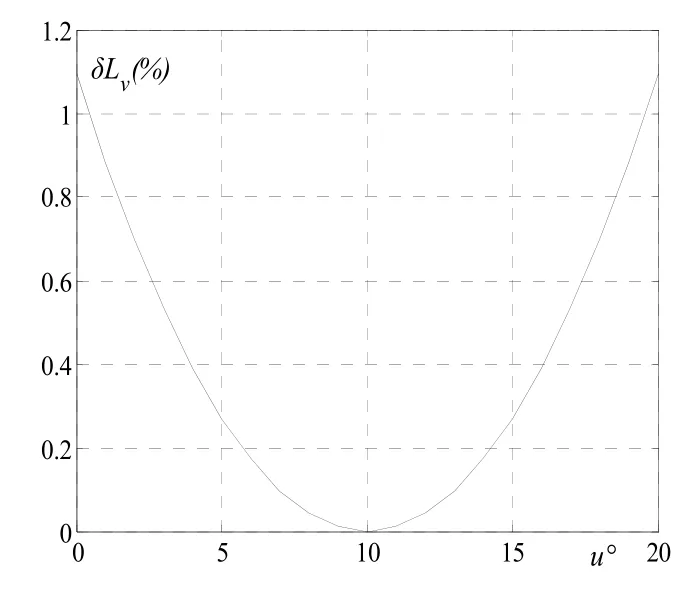
圖6 經線長度相對變化曲線

圖7 參數曲線交角的相對變化曲

4.2.2 局部變形分析

把 f( v)=R + r cos v 、g ( v)=r sinv和切柱面的第一基本量代入公

式（11），得到映射中的微分長度比

式中

圖8和圖9分別為由上式得到的u = 5°,v = 45°、90°、135°和u = 15°,v = 45°、90°、135°時的μ- β曲線，由公式和圖可知：

1）μ( u, v, β) =μ( u, v ,180°+ β)，即在一點處隨著方向角β的變化，μ是以π為周期的周期函數。

2） 隨著方向角β變化一周，μ四次取得極值，如圖8中v = 90°的曲線，μ在極值方向角β等于43.7476°和223.7476°時取最大值1.0487；在133.7476°和313.7476°時取最小值0.9609，極值方向角對應著過該點的極值映射曲線的切矢方向，各極值方向角間相隔90°。

3） 隨著方向角β變化一周，μ四次取 1值，如圖8中v = 90°的曲線，μ在方向角β為92.4630°、175.0000°、272.4630°和355.0000°時等于 1，4個等距方向角對應著過該點的等距映射曲線的切矢方向。

4）μ( u, v, β)=μ( u ,180°- v,β)，如圖中v=45°與 v=135°的曲線重合，即μ在 v向參數對稱于 π /2時具有相同的值。

5）μ( u, v, β) =μ( 20°- u, v ,180°- β)，如圖中 μ(5°, 90°,0°) =μ(15°, 90°, 180°) =1.0077，即μ在 u向參數和方向角β均對稱于Γ曲線(u=U=10°)時具有相同的值。

圖8 u=5°時的微分長度比

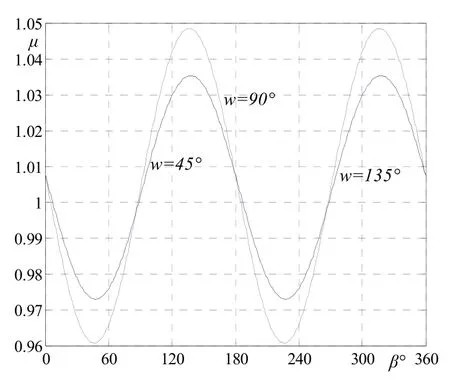
圖9 u=15°時的微分長度比

圖10和圖11是由公式（15）和公式（16）得到的過點u = 5°和20°，v =30°、50°、…、150°的極值和等距映射曲線。由圖10，圖11可見，過每點分別各有兩條極值映射曲線和等距映射曲線。根據一點處微分長度比的變化，圖 10中向上傾斜的為最大變形曲線，向下傾斜的為最小變形曲線，分別對應著該點處最大和最小微分長度比的方向；圖 11中過各點的兩條等距映射曲線在展開時長度不發生變化，它們對應著該點處微分長度比等于1的方向。圖12為把極值映射曲線和等距映射曲線變換到環面上的情形。

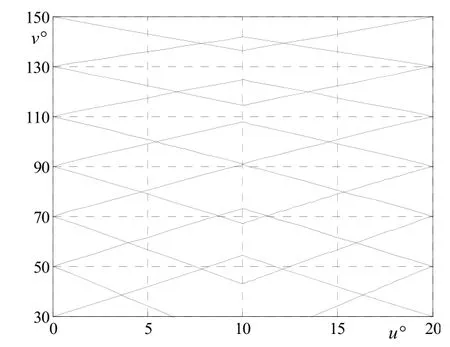
圖10 極值映射曲線

圖11 等距映射曲線

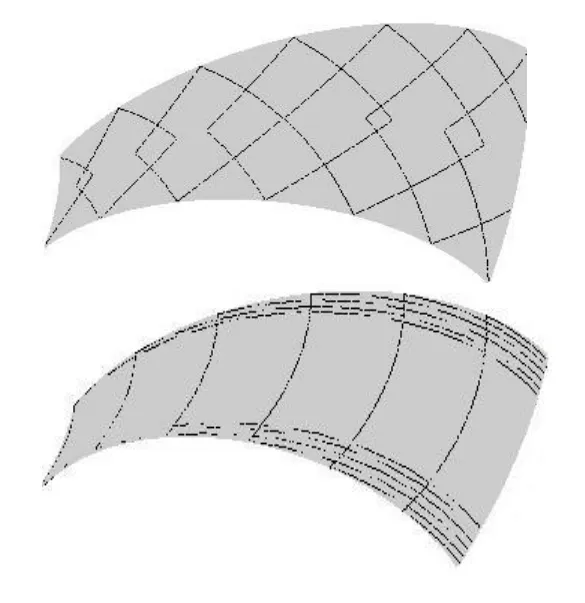
圖12 環面上的極值和等距曲線

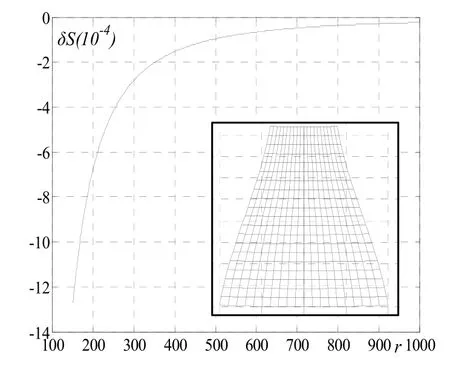
圖13 S rδ - 曲線和校正后的展

由上面分析可見，曲面展開后緯線和經線長度都變長（因各點在0°和90°的微分長度比均大于1），導致展開后面積增大；緯線長度的相對變化與參數v（即緯度）無關，且與面積的相對變化等值，當u2=20°時為0.0103；經線長度的相對變化在u=20°時也達到0.0109，因而在用切柱面片對環面片進行替代時，經度方向不易取過大的范圍，以減小展開誤差。

以上分析為展開樣板的矯正提供了依據，可采用形狀與面積并行矯正，形狀矯正為主、面積矯正為輔的策略：首先矯正緯線長度，使各緯線長度變化為零，由于面積相對變化只與緯向參數相關，所以緯線校正后，面積相對變化也趨向于零；然后再進行經線的矯正，把各緯線由平行線矯正為同心圓弧，各弧長等于相應緯線實長，大、小端圓弧的半徑差等于經線實長，經線矯正會引起面積相對變化值的改變，形成面積相對變化與同心圓半徑間的函數關系；最后根據這個函數關系，在合理控制面積相對變化值的情況下確定同心圓半徑，從而完成展開樣板的矯正。圖 13是面積相對變化與大端圓弧半徑r間的關系曲線和校正后的展開圖，其面積相對變化值取為負0.001，這時大端圓弧半徑為166.9680mm。

5 結 束 語

在上面的論述中，系統地提出了構造回轉曲面的可展切曲面及它們間映射分析的理論與方法，建立了回轉曲面可展切柱面和可展切錐面的數學模型，建立了它們間的映射關系，基于提出的回轉曲面及其可展切曲面間微分長度比的理論分析，推出了映射中極值映射曲線和等距映射曲線的微分方程，通過整體和局部的變形分析，可以準確地掌握回轉曲面與其可展切曲面間映射中的變形情況。這些理論和方法可以在曲面結構設計、不可展曲面近似展開及其誤差分析和紋理映射及其變形控制等方面得到應用，同時對于曲面間映射分析的其他場合也有一定的借鑒、推廣價值。

[1] 孟雅琴. 可展曲面的構造與插值研究[M]. 上海:上海交通大學出版社, 2010:3-25.

[2] Aumann G. A simple algorithm for designing developable Bezier surfaces [J]. Computer Aided Geometric Design, 2003, 20(8/9):601-619.

[3] Chalfant J S, Maekawa T. Design for manufacturing using B-spline developable surface [J]. Journal of Ship Research, 1998, 42(3):207-215.

[4] Pottmann H, Wallne J. Approximation algorithms for developable surfaces [J]. Computer Aided Geometric Design, 1999, 16(6):539-556.

[5] 毛 昕, 侯 悅. 不可展回轉曲面近似展開的精度分析[J]. 工程圖學學報, 1998, 19(3):1-10.

[6] 毛 昕, 侯 悅. 回轉曲面近似展開的數學模型[J].工程圖學學報, 1999, 20(4):1-6.

[7] 丁 森. 不可展曲面近似展開中若干問題的研究[D].沈陽:東北大學, 2011.

Developable Tangent Surface of Rotary Surface

Mao Xin, Yang Jinglin, Ma Mingxu
( Northeast University Mechanical Engineering and Automation School , Shenyang Liaoning 110004, China )

The general theory and method to construct the developable tangent curved surface of rotary surface and mapping analysis between them are put forward systematically, the mathematical model and mapping relationship of the developable tangent cylinder and developable tangent cone of rotary surface are established. The differential equations of the extreme value mapping curve and equidistant mapping curve are put forward according to the theory of differential length ratio between the rotary surface and its developable tangent curved surface. The deformation of mapping will be grasped accurately by the whole and local deformation analysis.

geometry calculation; rotary surface; developable tangent curved surface; mapping analysis

TB 21

A

2095-302X (2013)02-0065-07

2012-04-23；定稿日期：2012-05-07

毛 昕（1954-），男，吉林長春人，教授，碩士，主要研究方向為計算機圖形學及輔助設計、理論與應用圖學。E-mail：ddmx54@sina.com