視圖中呈類似性同一平面的可構性研究

董 萍

（蘇州市職業大學機電工程學院，江蘇 蘇州 215104）

視圖中呈類似性同一平面的可構性研究

董 萍

（蘇州市職業大學機電工程學院，江蘇 蘇州 215104）

針對視圖中呈類似性同一平面的可構性，分別研究了視圖中呈類似性投影面垂直平面及一般位置平面，可構分兩種情況，一是視圖中呈類似性同一平面輪廓線是否可構，二是當視圖中呈類似性同一平面其輪廓線不可構時，輪廓包圍區域是否構形。視圖中呈類似性同一平面，不論是幾邊形平面，在已知二視圖時，組成面的輪廓中呈類似性投影面平行線均可構，當輪廓線可構時，構形的方法也多樣化。二視圖中呈類似性的投影面垂直平面可構，三視圖中一般位置平面仍可構。

視圖；類似性；可構性；投影面垂直平面；一般位置平面

針對視圖中呈類似性的同一平面的可構性進行研究，發現文獻[1]所指的兩面多框可構視圖中存在不可構表面的條件，即視圖中呈類似性的同一平面均可構[2]，文獻[2]對研究對象為平面的幾例作了認真研究。

投射線垂直于投影面的投影方法稱為正投影法，由正投影法得到的投影，稱為正投影，簡稱為投影[3-6]。

正投影法投影特點：

1） 真實性。當物體上的平面（或直線）與投影面平行時，其反映實形（或實長），這種投影特性稱為真實性。

2） 積聚性。當物體上的平面（或直線）與投影面垂直時，則在投影面上的投影積聚為一條線（或一個點），這種投影特性稱為積聚性。

3） 類似性。當物體上的平面（或直線）與投影面傾斜時，則在投影面上的投影變小（或長度變短），但投影形狀仍與原來形狀類似，這種投影特性稱為類似性[3-6]。

按照國家標準《機械制圖》的規定，工程上把用正投影法所繪制出的圖形叫做視圖，可得到機件三視圖，分別稱為

主視圖—正面（V）投影；

俯視圖—水平（H）投影；

左視圖—側面（W）投影[7]。

二視圖則為三視圖中任意兩個視圖。

針對視圖中呈類似性同一平面的可構性進行深入研究，取得了如下進展。進展

1 視圖中呈類似性同一平面，不論是幾邊形的面，在已知二投影圖時，組成面輪廓中呈類似性投影面平行線均可構。

進展2 研究視圖中呈類似性同一平面的可構性，不僅要研究視圖中呈類似性同一平面的輪廓線是否可構，還要研究組成平面輪廓包圍的區域是否可構。后者是研究視圖中呈類似性同一平面的可構性突破性進展，至于前者，不僅如進展一所述，而且構形的方法也有創新。構形結果使滿足視圖結果的物體形狀千變萬化。

視圖中呈類似性同一平面的可構分兩種情況：1）

構成平面輪廓線中有呈類似性投影面平行線時可構，其面亦相應變化；或其輪廓不變，對輪廓包圍的區域構形；2）

構成平面的輪廓線不可構（構成面的線中無投影面平行線），但輪廓包圍的區域可構。以往研究僅局限于研究組成平面輪廓線可構與否，現還考慮到輪廓包圍區域的可構性。視圖中呈類似性同一平面（下文中所提及的面均指平面）分為：投影面垂直面及一般位置面。

1 視圖中呈類似性投影面垂直面的可構性

1.1 二視圖中呈類似性投影面垂直面的可構性

1.1.1 構成投影面垂直面輪廓線中無呈類似性投影面平行線時，可對輪廓包圍的區域構形。如圖

1所示，已知主俯視圖，見圖1(a)，其 A面不變的部分構形部分側面投影見圖1(b)～圖1(e)。

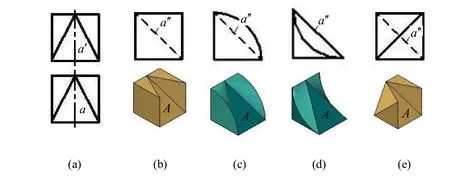
圖1 已知主俯視圖的不同左視圖（A面不變的部分構形）

投影面垂直面A的兩個投影呈類似三角形，且構成A面輪廓線中無呈類似性投影面平行線，但可對構成 A面輪廓包圍區域構形。以圖 2(b)為例，構圖結果如圖2(c)所示，A面定義域為投影滿足已知條件圖2(a)中的三角形空間點集，有無窮多構形方法。，

圖2 構成A面輪廓線中無呈類似性投影面平行線時，可對輪廓包圍的區域構形

圖1(b)～圖1(e)中的構成A面輪廓包圍區域亦可構形。

1.1.2 構成投影面垂直面輪廓線中有呈類似性投影面平行線時，投影面平行線可構；或其輪廓不變，對輪廓包圍區域構形。如圖

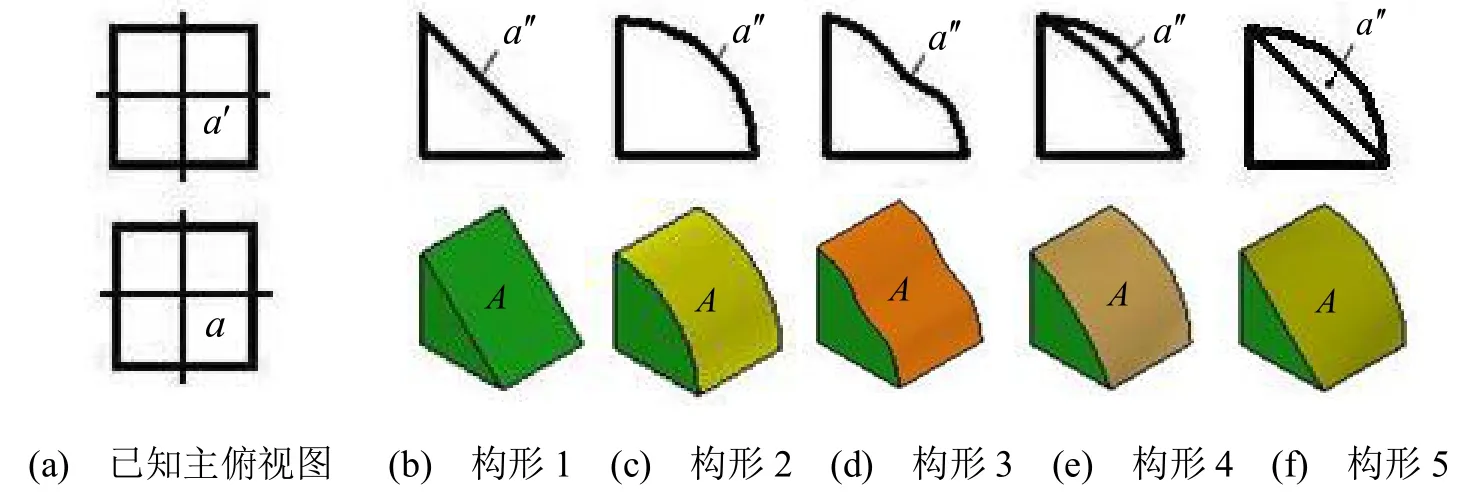
圖3 二視圖中構成A面的輪廓線中有呈類似性的投影面平行線時，可對其構形

3(a)所示，已知主俯視圖，其左視圖有無窮多構形方法，圖3(b)就是其中之一，因構成A面的輪廓線中左右兩條為類似性的側平線，所以可構，圖3(c)～圖3(e)是部分構形，圖3(c)是兩條側平線一致的簡單構形（通常構法），圖3(d)中兩條側平線構形盡管一致，但側平線是幾條圓弧段組合（亦可若干直線段與圓弧段等組合），構成曲面 A的所有公切面應傾斜于投影面；圖3(e)是構成A面輪廓線中左右兩條側平線采用不同的構形方法；圖3(f)則是左側的側平線不變，對右側的側平線構形。

總之，對左右兩條側平線的構形方法很多，其定義域為滿足圖3(a)的空間點集，有無窮多種構形方法。除了

對側平線構形（當然，A面亦相應改變）外，還可以構成A面的輪廓線不變，即側平線不變，僅對A面輪廓包圍的區域構形，已知條件圖4(a)，對圖4(b)中A面的輪廓包圍的區域構形，構形結果之一如圖4(c)所示，其構形方法很多，定義域為滿足圖4(a)的空間點集。

在圖4(c)構形的基礎上還可以繼續構形，如：右側面上側平線采用多段相切的線段（直線段、圓弧線段、橢圓弧線段及任意弧狀線段組合），條件是滿足投影要求，當然，亦可右側輪廓線不變，僅對左側輪廓線構形。同理，圖3(c)～圖3(f)亦可以再構形。除此之外，還可以先對上述側平面構形，再對構成A面的輪廓包圍區域構形等等[8]。

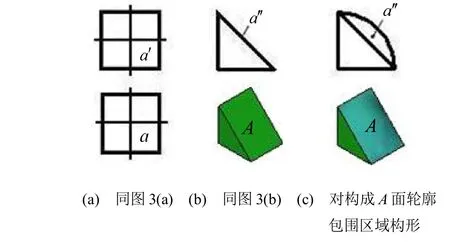
圖4 除對構成A面的輪廓線中呈類似性的投影面平行線構形外，還可對輪廓包圍區域構形

如圖5所示，圖5(a)已知主左視圖，P面（六邊形）為鉛垂面，且其輪廓線中水平線MN的兩投影呈類似性，則MN可構，圖5(b)MN為直線段，圖5(c)MN為圓弧段，P面亦相應變化；或圖5(b)中P面輪廓不變，對P面輪廓包圍的區域構形，如圖5(d)所示，有無窮多解，其定義域如前所述。當然，還有其他構形方法。

視圖中呈類似性的投影面垂直面，不論是幾邊形，在已知二視圖時，組成平面的輪廓中呈類似性投影面平行線均可構，輪廓包圍的區域相應變化；或組成面的輪廓不變，對面輪廓包圍的區域構形，亦可兩者組合構形。

圖5 二視圖中構成面的輪廓線中有呈類似性的投影面平行線時，可對其或輪廓包圍區域構形

1.2 三視圖中呈類似性投影面垂直面可構性

如圖6所示，已知三視圖，投影面垂直面A在主俯視圖中呈類似性，在左視圖中呈積聚性，所以，圖6(a)中的A面不可構；圖6(b)中的B面同樣不可構。

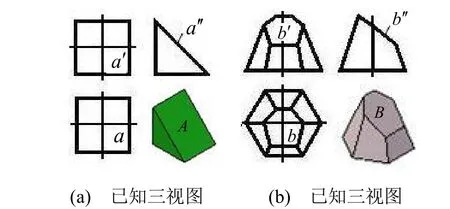
圖6 已知三視圖時，投影面垂直面不可構

2 視圖中的同一一般位置面的可構性

2.1 二視圖中的同一一般位置面的可構性

2.1.1 二視圖中一般位置面的輪廓中不包含呈類似性投影面平行線的可構性

二視圖中一般位置面的輪廓中不包含呈類似性投影面平行線，一般位置面的輪廓線不可構，但其輪廓包圍的區域可構，如圖7所示。

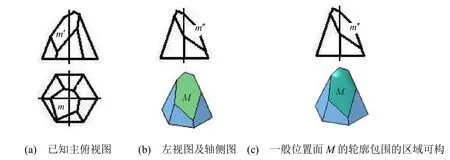
圖7 構成M面的輪廓線中無呈類似性的投影面平行線時，可對M面輪廓包圍的區域構形

盡管組成M面的輪廓線中無側平線，但其包圍的區域可構，其定義域為滿足圖7(a)的空間點集，有無窮多解，其中二解如圖7(b)及圖7(c)所示。

2.1.2 二視圖中同一一般位置面輪廓中包含呈類似性投影面平行線的可構性

如圖8所示，圖8(a)已知主俯視圖，一般位置面A輪廓線中CD為側平線，且呈類似性，則CD可構，通常構圖結果2例，如圖8(b)及圖8(c)，圖8(d)為側平線CD的一例組合構形。

除了CD構形外，還可以對A面輪廓包圍的區域構形，圖8(e)是對圖8(b) A面輪廓包圍區域的構形結果。

無論是對側平線CD構形，還是對A面輪廓包圍的區域構形，均有無窮多解，定義域如前所述。

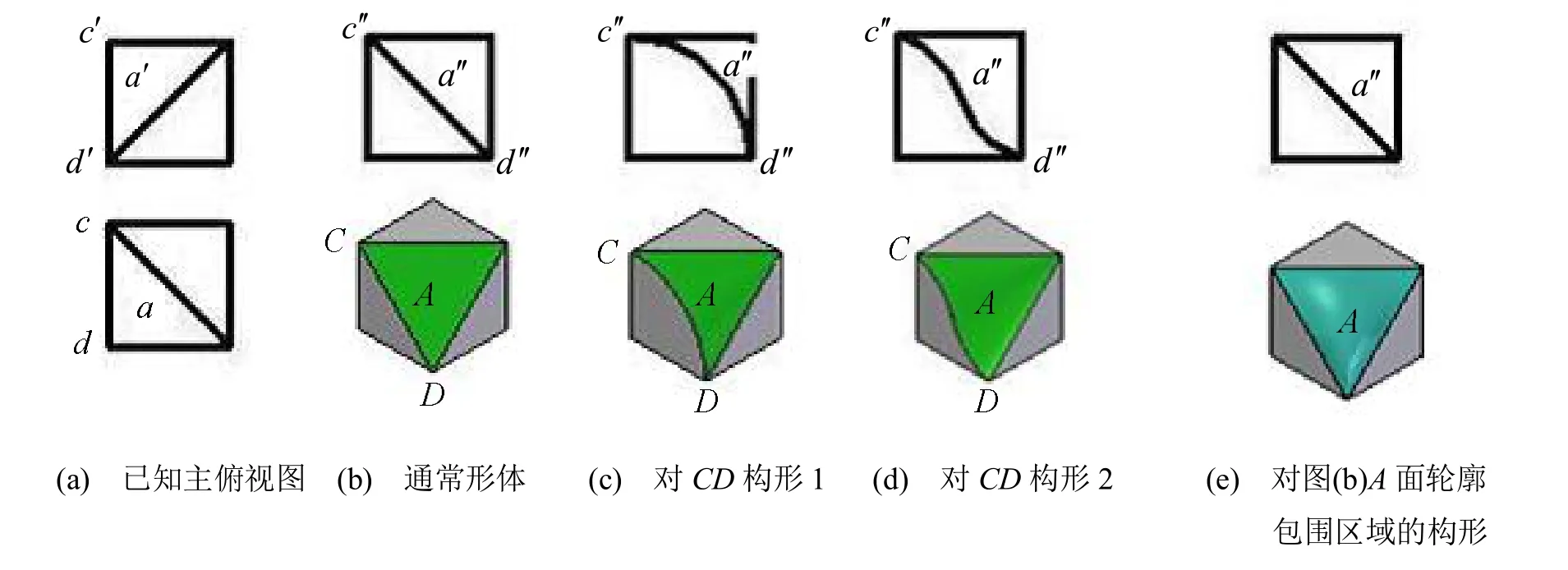
圖8 已知二視圖，對一般位置面A的輪廓線中呈類似性的投影面平行線CD及A面輪廓包圍的區域構形

如圖9所示，圖9(a)已知俯左視圖，一般位置面Q的輪廓線中CD為正平線，且呈類似性，則CD可構，部分構圖結果如圖9(b)、圖9(c)及圖9(d)所示，或Q面輪廓不變，可對Q面輪廓包圍的區域構形，圖9(e)及圖9(f)是對圖9(b)包圍區域構形的部分結果。無論是對側平線CD構形，還是對Q面輪廓包圍區域構形，均有無窮多解，定義域如前所述。

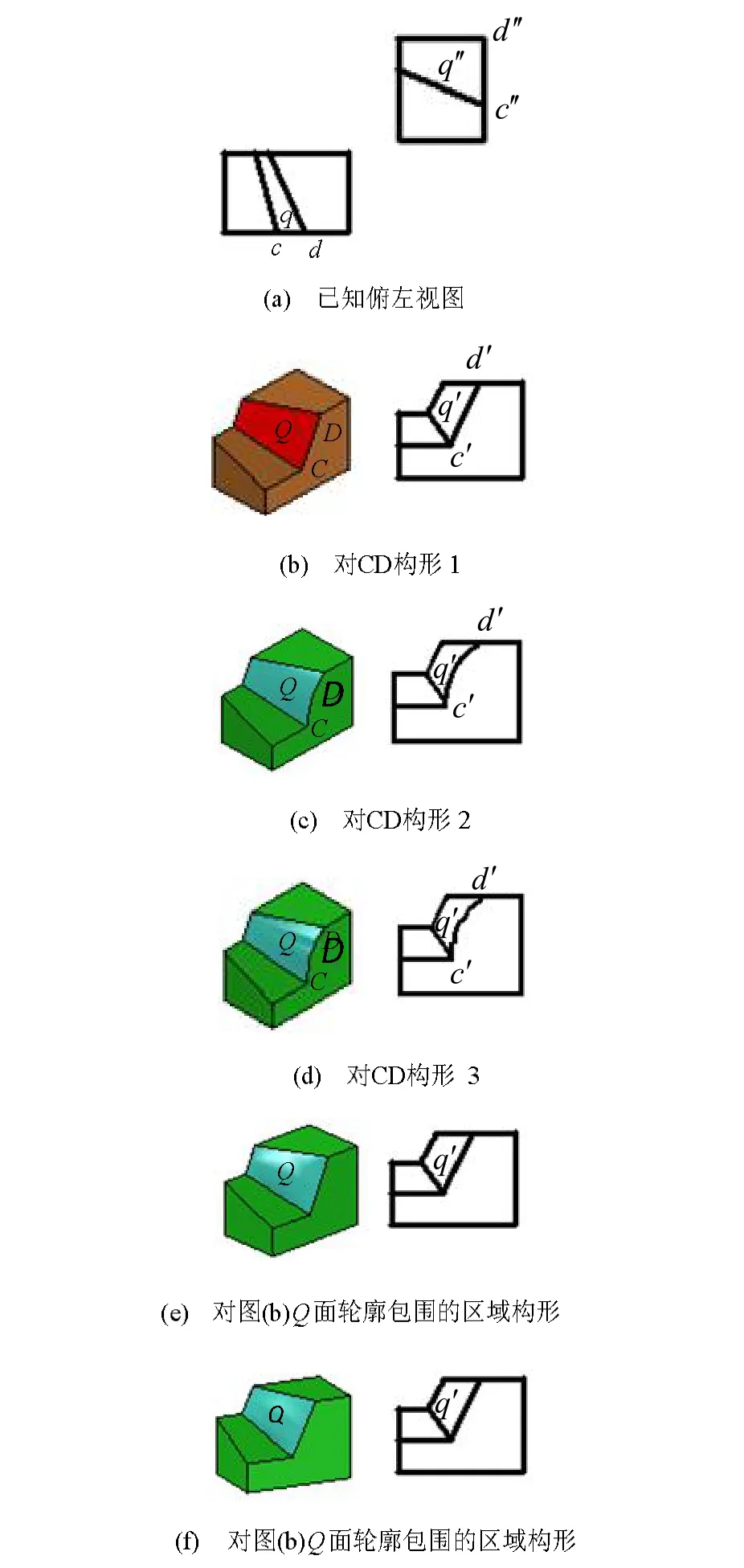
圖9 已知二視圖，對一般位置面Q的輪廓線中呈類似性的投影面平行線CD或Q面輪廓線包圍的區域構形

2.2 三視圖中一般位置面的可構性

已知三視圖，無論構成一般位置面的輪廓線中有無呈類似性的投影面平行線，輪廓線均不可構，但輪廓包圍的區域仍可構。

如圖10所示，圖10(a)，已知三視圖，一般位置面 P一般考慮為平面，基本軸側圖見圖10(b)，研究結果，P面可構。盡管組成P面的輪廓不可構，但組成 P面的輪廓線包圍的區域可構，構圖幾例如圖10(c)～圖10(e)所示。其定義域為滿足圖 10(a)中三視圖的空間點集，有無窮多解。

同理，如圖11、圖12所示，圖11(a)及圖12(a)均已知三視圖，其一般位置面A及一般位置面M仍可構，其構形結果是平面變為曲面，各自構形一例分別如圖11(c)及圖12(c)所示，A面及M面輪廓線包圍區域構形定義域分別為滿足圖 11(a)及圖12(a)中三視圖的空間點集，均有無窮多解。

從圖10、圖11及圖12可以看出，盡管已知三視圖，其形體仍不確定，因投影圖上的一般位置面仍然是可構的，且構形方法很多。

圖10 已知三視圖，一般位置面P輪廓包圍的區域仍可構

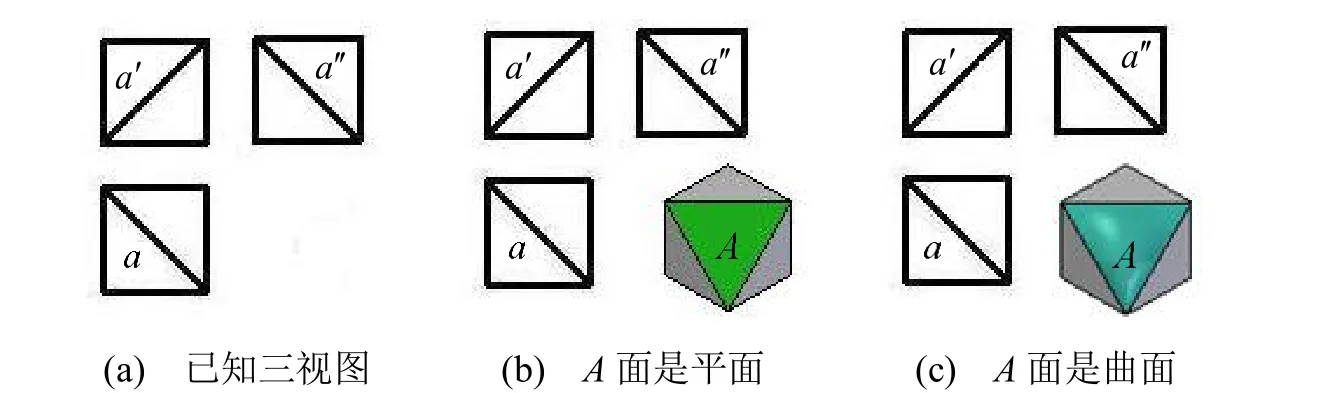
圖11 已知三視圖，一般位置面A輪廓包圍的區域可構

圖12 已知三視圖，一般位置面M輪廓包圍的區域可構

3 結 束 語

綜上所述，二視圖中呈類似性的投影面垂直面可構，三視圖中的一般位置面可構。

二視圖中呈類似性同一面輪廓線中呈類似性投影線可構（且與組成面輪廓線的條數無關，另外，可構輪廓線形狀可以變化多樣）時，其面亦相應變化；或其輪廓不變，僅輪廓包圍區域構形；還可以反復構形，或兩者組合構形。

二視圖中呈類似性同一面輪廓線中無呈類似性投影線時，可對輪廓線包圍區域構形。

三視圖中一般位置面輪廓線不可構，但輪廓線包圍區域可構。

[1] 周宗團, 曹 敏, 陳翔鶴. 兩面多框可構視圖中存在不可構表面的條件[J]. 工程圖學學報, 2010, 28(3): 155-160.

[2] 董 萍. 形體上同一個面的兩個投影呈類似形的可構性研究[J]. 電子世界, 2012, 414(12): 91-91.

[3] GB/T 13361-2012. 機械制圖通用術語[S].

[4] GB/T 24739-2009. 機械制圖機件上傾斜結構的表示法[S].

[5] GB/T 16948-1997. 技術產品文件 詞匯 投影法術語[S].

[6] 胡 琳, 程 蕾, 付 苓. 工程圖學(第2版)[M]. 北京: 機械工業出版社, 2010: 20-30.

[7] 魏增菊, 李莉主編. 機械制圖[M]. 北京: 科學出版社, 2007: 37, 61.

[8] 董 萍. 運用TRIZ創造性原理拓寬構圖思路初探[J].電子世界, 2012, 410(10): 89-89.

Structuralization of Similar Planes on the Views

Dong Ping
(Mechanical and Electrical Engincering College, Suzhou Vocational University, Suzhou Jiangsu 215104, China )

The similar vertical plane of projection plane and the similar incline plane on the views are studied respectively. Two situations are discussed. One is when the contour line of the similar same plane can be constructed, and the other is when it can not be constructed. In either situation, the planes are both constructable.

views; accumulation; structuralization; vertical projection plane; incline plane

TH 126

A

2095-302X (2013)05-0148-06

2013-01-20；定稿日期：2013-05-29

董 萍（1958-），女，江蘇泰州人，講師，主要研究方向為理論圖學、應用圖學、CAD及機械設計等。E-mail：dp@jssvc.edu.cn