電動負載模擬器抑制多余力的結構補償控制

李瑞，王明艷

(中北大學信息與通信工程學院，山西太原030051)

在科學研究中，為了測試產品的性能指標，需要模擬出對象的實際工作環境，對產品施加與實際情況相對應的負載，從而真實地反映產品實際的性能，這就需要研制出高性能的加載系統，以便為新材料和產品的應用、為新技術的推廣提供可靠的實驗資料[1]。按照加載執行元件的不同，可分為機械式負載模擬器、液壓式負載模擬器和電動式負載模擬器。

由于電液負載模擬器的污染大，維修困難，近年來，隨著電機性能的不斷提升、電力電子器件、電機驅動系統的發展、電機制造水平的提高，越來越多的伺服控制系統以永磁同步電動機作為執行元件，因此必須采用電動加載方案。電動負載模擬器對于縮短系統研制周期、節約研制經費、提高可靠性和成功率有著重要意義[2]。

1 電動負載模擬器系統硬件組成

一個完整的電動負載模擬器應由加載電機、扭矩傳感器、聯軸器、驅動器、控制器、上位機等幾部分組成，如圖1所示。

圖1 電動負載模擬器結構框圖

控制器接收仿真計算機發出的指令信號及扭矩傳感器發回的力矩反饋信號，利用給定的控制算法計算出下一時刻的控制量，通過驅動器作用在加載電機上，產生相應的力矩輸出施加到舵機上，扭矩傳感器再將作用在舵機上力矩值實時反饋給控制器，為計算下一時刻控制量提供依據。

2 系統模型的建立

加載電機模型。加載電機選擇永磁直流力矩電機，可以使得電動加載系統獲得良好的動態、靜態性能。

直流力矩電機的電壓平衡方程為:

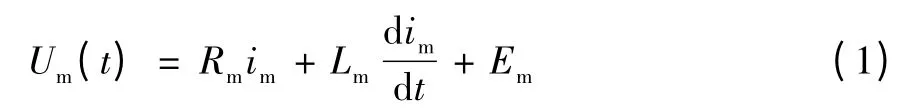
式中:Em為電樞反電動勢，它是當電樞旋轉時產生的反電勢，其大小與激磁磁通及轉速成正比，方向與電樞電壓Um相反。則反電動勢Em可以寫為:

直流力矩電機的轉矩平衡方程為:

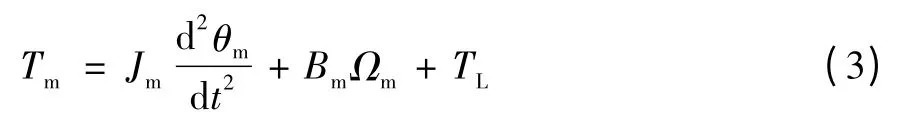
電磁轉矩Tm可表示為:

式中:Um為電樞電壓，KT為轉矩系數，Ke為反電動勢系數，Rm為電樞回路總電阻，Lm為電樞回路總電感，Ωm為電機角速度，θm為電機角位移，Bm為電機阻尼系數，Jm為等效轉動慣量，im為電樞電流。

轉矩傳感器模型。轉矩傳感器連接加載電機和舵機的輸出軸，可將傳感器兩端的微小角度形變轉化為轉矩信號輸出。假設傳感器的剛度系數為Kf，傳感器兩端的角度差Δθ=θm－θr，則輸出的轉矩可表示為:

PWM 驅動裝置模型。PWM變換器是具有飽和特性的擬線性放大器，當大功率晶體管的開關頻率遠遠大于電動機的工作頻率時，PWM 驅動裝置的輸出信號中交流分量的影響很小，可以近似認為PWM 驅動裝置為一個比例環節，其放大倍數為KPWM。

由以上表達式可得電動加載系統的動態結構圖，如圖2所示。

圖2 電動加載系統動態結構圖

由圖2可得加載電機輸出轉矩的傳遞函數表達式為:

其中:

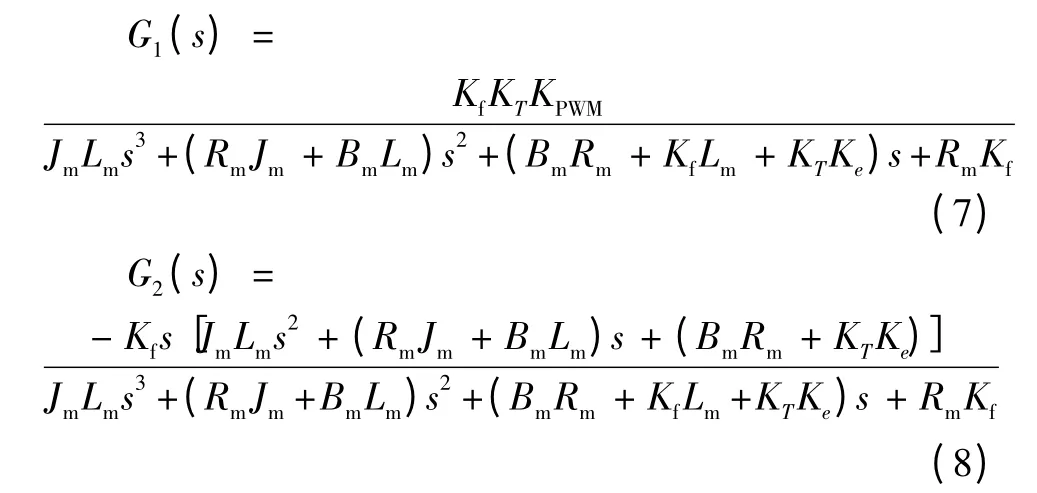
可見:輸出力矩由兩部分組成，后一部分帶有明顯的微分特性，被加載對象的角速度、角加速度、角加速度的變化率的擾動引起，這就是所謂的多余力矩[3－5]，多余力矩的存在會破壞加載電機對給定載荷曲線的跟蹤精度。

3 消除多余力矩

文中采用結構不變性原理來消除多余力矩，使用雙通道正負抵消，進行前饋控制來消除多余力矩，并分析以下兩種消除多余力矩方法的局限性，提出改進的結構不變性原理來消除多余力矩。

3.1 被加載對象角位移前饋補償法

對于電動負載器來說，最直接的擾動補償是利用被加載對象的角位移本身進行補償。系統結構圖如圖3所示。

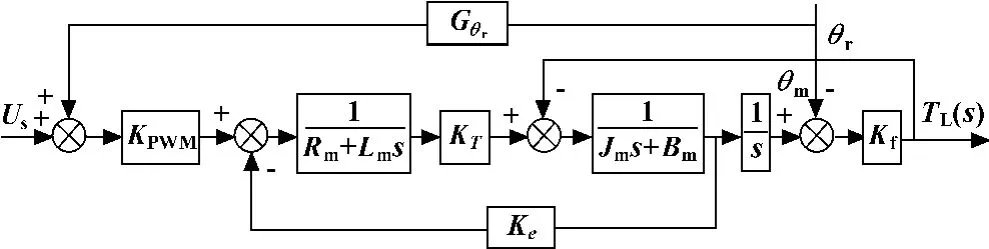
圖3 角位移前饋補償法結構圖

由結構圖和結構不變性原理可以得到:

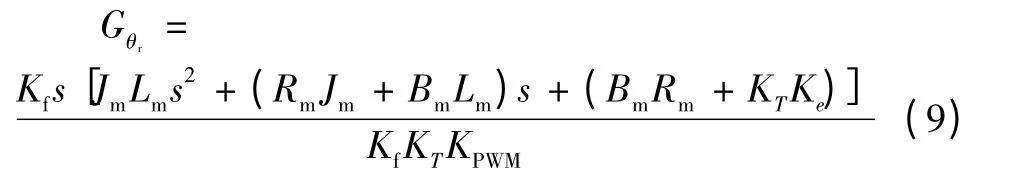
多余力矩可以完全被抑制，但事實上Gθr的實現有一定的難度，因為高階的純微分環節容易引入干擾。加入補償環節后，大部分多余力矩可以被消除。

3.2 負載模擬器電流反饋補償法

電流Im反饋擾動補償法，就是為了降低系統的微分階數。系統結構圖如圖4所示。

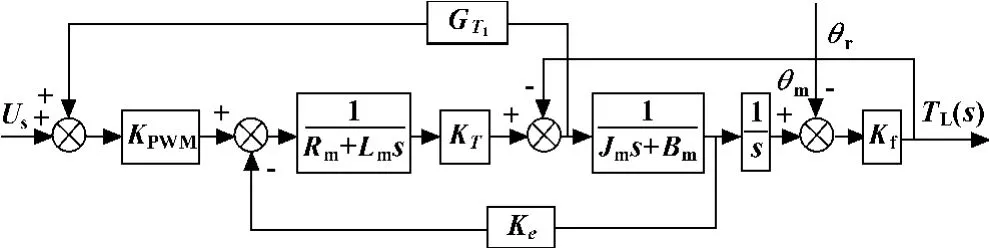
圖4 電流反饋補償法結構圖

在設計補償環節時，負載等效剛度比較大，在低頻段加載中可以近似認為負載模擬器的角速度等于被加載對象的角速度[6]。

代入上式可得:

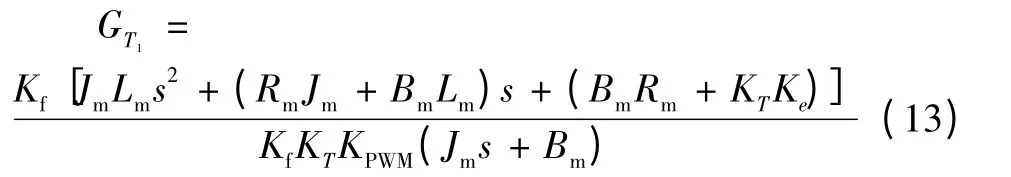
實際上，基于結構不變性原理的被加載對象角位移前饋補償法，是用角位移信號微分得到速度信號，然而微分得到的加速度信號和相位滯后嚴重影響了信號質量。對于負載模擬器的角速度反饋補償法，由于要求速度近似相等，事實上有一定的條件，需要剛度無窮大。限制了其應用，有一定的局限性。

3.3 被加載對象的電流前饋補償法

在抑制多余力矩的研究中，常規方法都著眼于加載系統，忽視了被加載對象系統。作者從電動負載模擬器和舵機兩部分出發，在被加載對象角位移前饋的基礎上，提出被加載對象電流前饋補償法，克服以上兩種方法的局限性，使補償環節微分階數降低兩階，降低了實現難度。系統框圖如圖5所示。

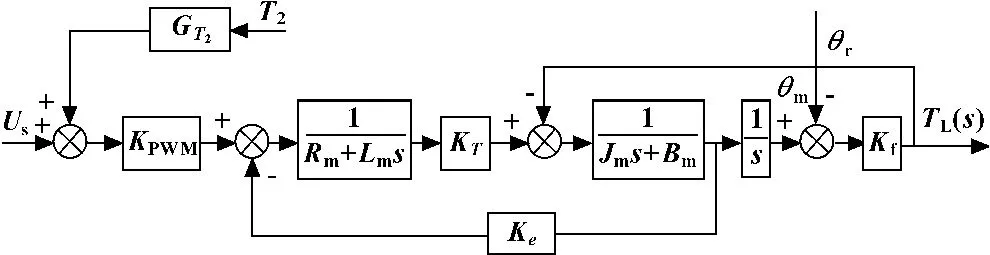
圖5 電流前饋補償法結構圖

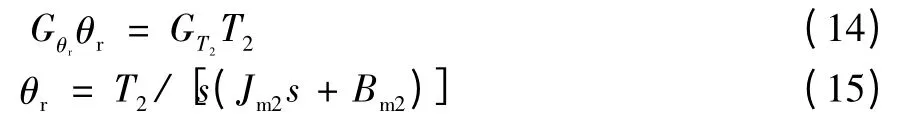
代入上式，可得:

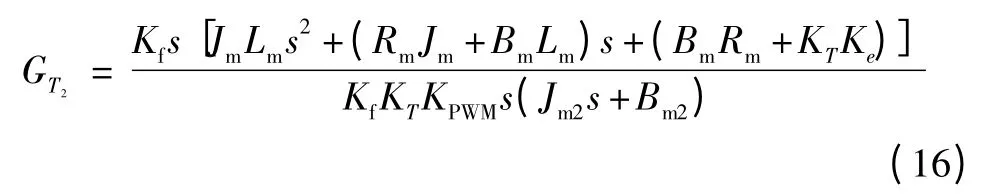
電動負載模擬器是一個復雜的機電一體化控制系統，雖然目前有神經網絡控制等智能控制理論的應用文獻介紹，但考慮到工程中的實際應用性，仍以成熟的PID控制來設計，同時采用輸出力矩變化速度負反饋來增加阻尼，降低超調量，提高系統的穩定性，基于被加載對象的電流前饋補償法來提高控制系統的快速性，減小多余力矩。

3.4 仿真分析

基于控制策略的介紹和分析，采用改進的前饋方法消除舵機運動在加載系統輸出上的擾動，用微分負反饋、力矩反饋、前向通道控制器的復合控制方法來設計系統。經過以上的系統分析，經過拉普拉斯變換，可得整個電動負載模擬器的控制結構原理圖如圖6所示。

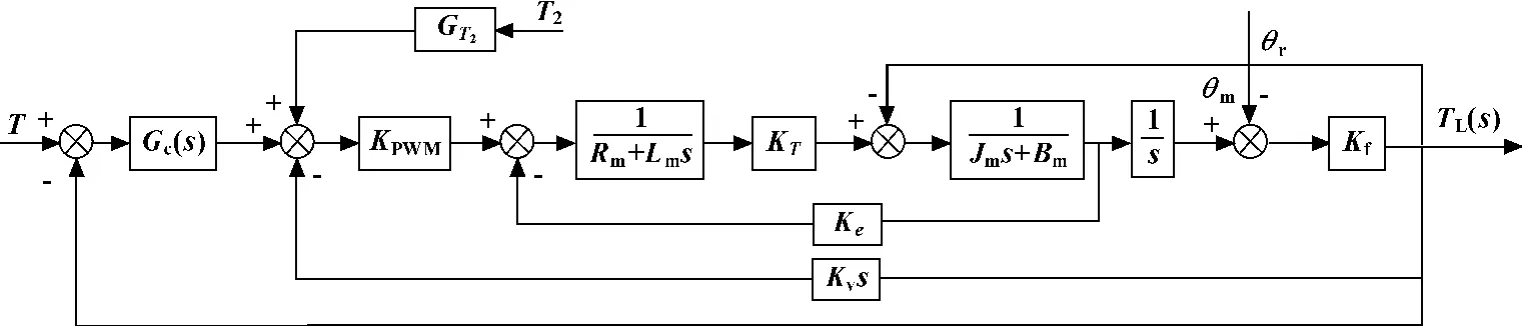
圖6 系統控制結構圖

參數如下:Rm=4.5 Ω，Lm=7 mH，Jm=0.15 kg·m2，Bm=0.33 m·s/rad，Ke=4.85 V·s/rad，KT=6 N·m/A，Kf=10 N·m/rad，Kv=0.05。

根據以上原理圖建模，動態測試結果如表1所示。

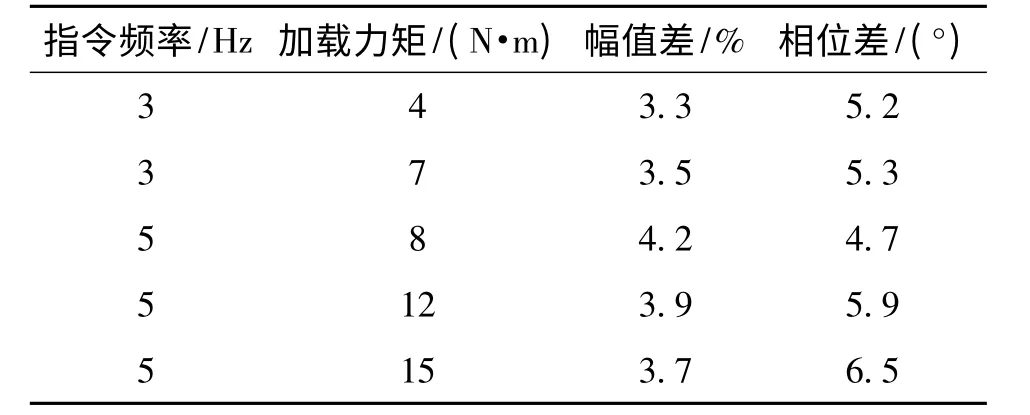
表1 動態測試結果

有舵機擾動，加入正弦信號的響應:

(1)給定信號為:T=4sin(6πt)，輸出與輸入結果如圖7所示。

(2)給定信號為T=6sin(10πt)，輸出與輸入結果如圖8所示。

根據以上仿真結果可以看出:加入改進的結構不變性原理的復合控制能夠很好地消除多余力矩，使輸出能夠快速穩定地跟蹤給定，減小了誤差，符合舵機加載系統的指標要求。

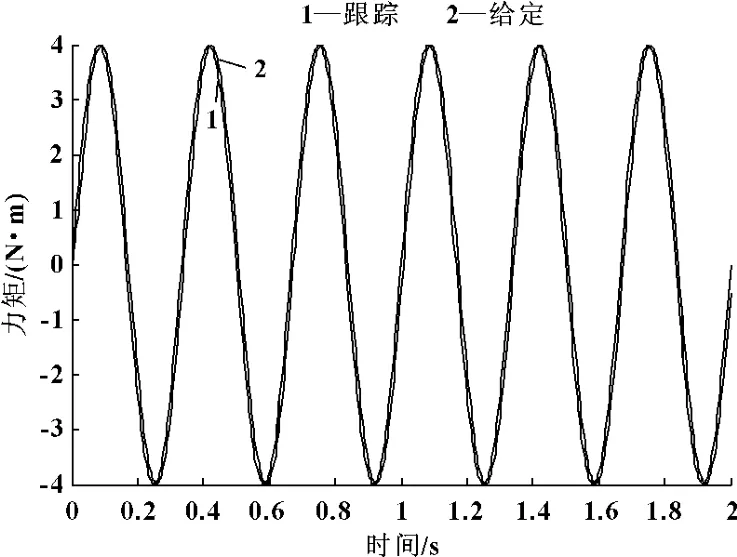
圖7 正弦響應圖(T=4sin(6πt))

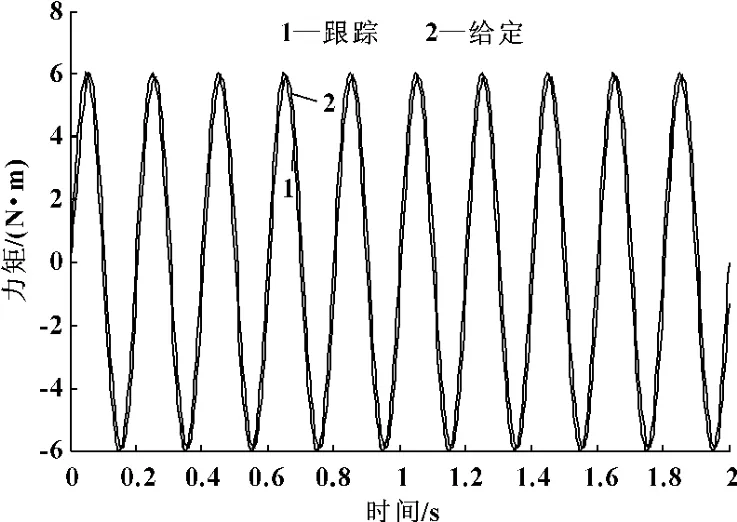
圖8 正弦響應圖(T=6sin(10πt))

4 結論

電動負載模擬器的多余力矩是由于舵機的位置擾動引起的，采用改進型結構不變性原理能夠很好地抑制擾動，誤差很小，滿足要求，而且基于控制算法的簡單性以及技術上的成熟性、可行性，在工程實際應用中有很好的參考價值。

【1】王述運.結構不變性原理在減搖鰭加載臺中的研究分析[D].哈爾濱:哈爾濱工程大學，2004.

【2】李成功，靳紅濤.電動負載模擬器多余力矩產生機理及抑制[J].北京航空航天大學學報，2006，32(2):204－208.

【3】鄒海峰.飛行器舵機電動伺服加載系統研究[J].系統仿真學報，2004，16(4):657－659.

【4】楊新峰，苑秉成.深彈舵機電動力加載控制系統的建模與仿真[J].計算機仿真，2010，27(1):13－17.

【5】馬志偉，杜經民，余祖耀.電動加載系統多余力特性分析[J].機床與液壓，2007，35(6):188－190.

【6】王明彥.電動負載模擬技術的研究[D].哈爾濱:哈爾濱工業大學，2004.