基于梯度校正法的非對稱液壓缸建模與參數辨識
謝建,李良,黃建朝
(第二炮兵工程大學,陜西西安710025)
在導彈起豎液壓系統中,液壓缸的行程較長,為節約空間都是采用非對稱液壓缸,并且這種液壓缸的加工、密封都比較簡單,制造成本也較低,更適合一些結構尺寸要求嚴格的導彈武器地面發射設備。但非對稱液壓缸兩腔的有效工作面積不等,因而正反向運動時,系統所需流量不等,各種參數與對稱缸差異很大,描述工作油路的數學模型也不同[1]。所以非對稱液壓缸建模問題是近年來國內理論界關注的一個熱點問題。
以往對于非對稱液壓缸的模型研究主要沿用對稱缸的方法,把重點集中在負載壓力和負載流量的定義上,其實質就是通過變量整合實現微分方程的整合[2]。由于這種方法不能反映系統結構因素對模型的影響,所以建模誤差較大。系統辨識和參數估計是一種建模的有效手段。作者用梯度校正法對閥控非對稱液壓缸系統進行了辨識,得到了其傳遞函數模型,并進行了算法的驗證,為起豎液壓缸控制的進一步研究奠定了基礎。
1 非對稱液壓缸模型的建立
在進行系統辨識之前,需要根據已經掌握的知識得到模型的結構。對于閥控非對稱液壓缸系統,可以利用液壓系統的相關理論和公式推導得到系統的數學模型,指導后面系統辨識和參數估計。
由比例閥的負載流量方程、液壓缸流量連續性方程和液壓缸力平衡方程得:
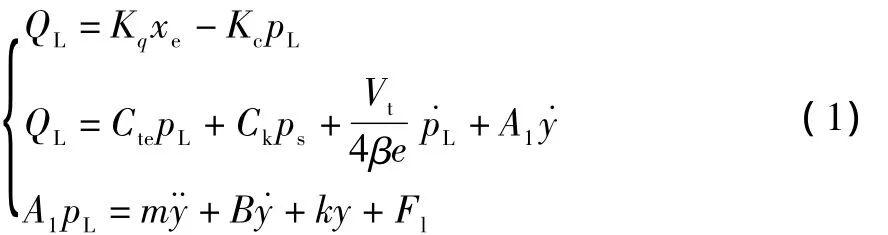
式中:QL為負載流量;pL為負載壓力;Cte為等效泄漏系數;Ck為附加泄漏系數;y為液壓缸位移;Vt為等效總容積;B為液壓缸等效阻尼系數;Fl為等效外負載力。
對式 (1)進行LapLace變換得:
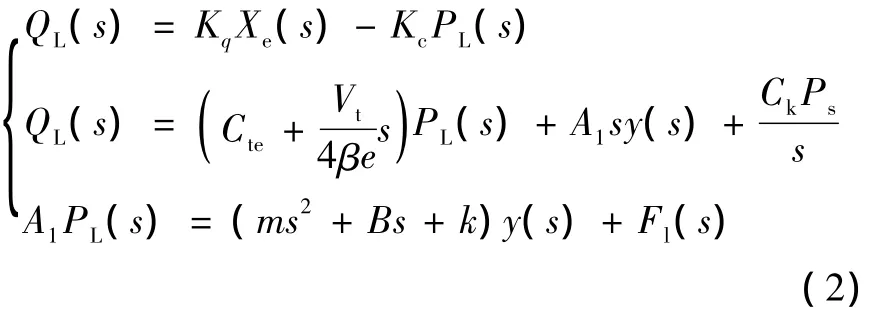
對式 (2)進一步簡化得:
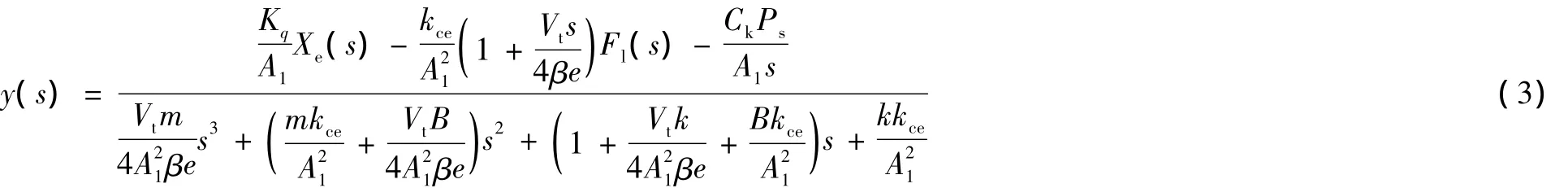
式中:kce為總流量壓力系數,kce=Kc+Cte。
閥控非對稱液壓缸系統以慣性負載為主,沒有彈性負載或彈性負載很小,因此可以認為k=0,則式(3)變為:

式中:ωh為閥控非對稱液壓缸系統固有頻率,ωh=;ξh為閥控非對稱液壓缸系統阻尼比,ξh=
由式 (4)可以看出,閥控非對稱液壓缸系統是一個三階系統。
2 梯度矯正參數估計的基本原理
梯度校正法的基本思想是:沿著準則函數 (目標函數)的負梯度方向,逐步修正模型參數估計值,直至準則函數達到最小值,該參數估計算法簡單易懂、實時計算量小。可以描述為:
根據前面的推導可知閥控非對稱液壓缸系統是一個三階系統,其離散傳遞函數可以描述為:
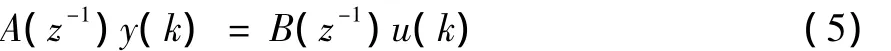
式中:u(k)和y(k)分別是系統的輸入和輸出;
A(z-1)=1+a1z-1+a2z-1+a3z-1;B(z-1)=b1z-1+b2z-1+b3z-1,a1,a2,a3,b1,b2,b3便是要估計的參數值。
式 (5)又可表示為:

式中:
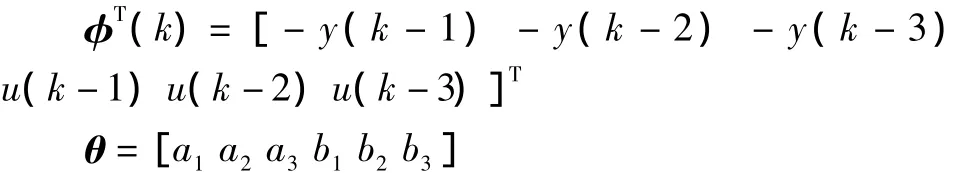
假設系統參數估計為:

上式γ的選擇應能夠使下式成立,即:
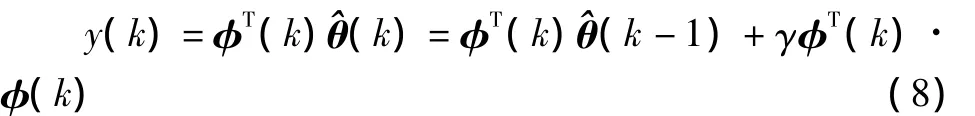
由式 (8)可以推出:
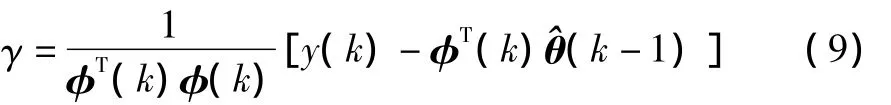
將式 (9)代入式 (7)得到:
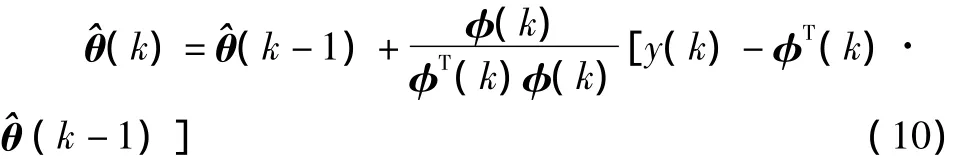
上式本質上是梯度校正法[3]。為避免φ(k)=0時算法不可行,式 (10)常修正為
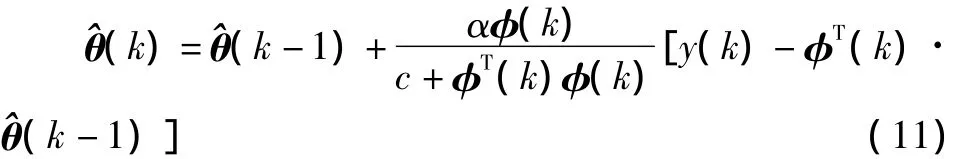
式中:c>0,0<α<2。
梯度校正參數估計的步驟如下:
步驟1,設置初值^θ(0)及參數c和α,輸入初始數據;
步驟2,采樣當前輸出y(k)和輸入u(k);
步驟3,利用式(11)計算^θ(k);
步驟4,k→k+1,返回步驟2,繼續循環。
3 非對稱液壓缸模型參數估計
3.1 輸入信號的選取
對于任何系統辨識算法,對輸入信號的選取都有一個基本原則:輸入信號必須持續激勵辨識系統的所有模態。若系統模型的結構正確,系統模型的辨識精度直接通過Fisher信息函數矩陣依賴于輸入來確定。因此,合理地選擇系統辨識的輸入信號是保證辨識精度的重要環節[4]。
系統辨識中廣泛采用的輸入信號有白噪聲序列、M序列、逆M序列。理論分析表明,選用白噪聲序列可以保證獲得較好的辨識效果。因為液壓系統對輸入信號的響應需要一定的時間,若輸入信號變化太快則系統不能跟隨上輸入信號,使得系統的辨識信息丟失,從而導致辨識的失敗,所以在每個白噪聲序列點延遲一定的時間,通過實驗確定延遲時間為0.3 s。輸入的白噪聲序列如圖1所示。
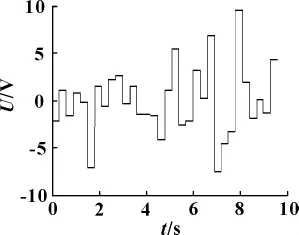
圖1 輸入白噪聲序列信號
3.2 實驗設計及數據采集
由于現在還很難得到關于導彈起豎液壓系統的有效數據,所以作者采用實驗室的FESTO液壓實驗平臺搭建閥控非對稱液壓缸系統來模擬起豎液壓系統。其實驗原理如圖2所示。
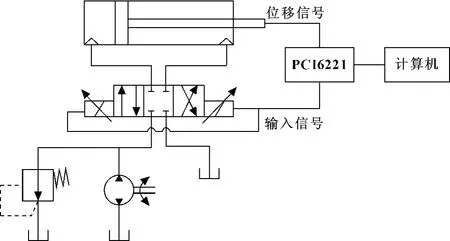
圖2 液壓實驗系統原理圖
采用NI公司的PCI6221作為數據采集設備,其分辨率為16位,最大采樣頻率為250 kHz,實驗所用頻率為1 kHz,即1 s內采集1 000個數據點。實驗中計算機通過LabVIEW平臺輸出白噪聲序列信號到采集卡PCI6221來控制電液比例閥,比例閥控制非對稱液壓缸的伸縮,液壓缸上裝有線性位移傳感器,通過PCI6221采集液壓缸的位移信號到計算機并存儲位移信號備用,位移信號為電壓信號,幅值為0~10 V,對應液壓缸的行程為0~200 mm。
3.3 參數辨識
用圖1中的輸入白噪聲序列信號,運行9.6 s,采集得到液壓缸的位移信號如圖3(a)所示,信號含有一定的噪聲,為了提高辨識的精度需對信號進行濾波處理,圖 (b)為濾波后的信號。
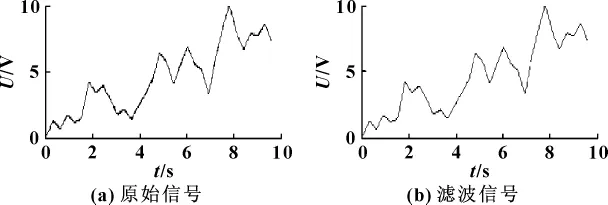
圖3 液壓缸位移信號
根據梯度校正法的基本步驟在MATLAB中編寫辨識算法,以圖1中的白噪聲序列為輸入信號,以圖3(b)中的液壓缸位移信號作為輸出信號進行參數辨識,最后得到閥控非對稱液壓缸的模型參數為:
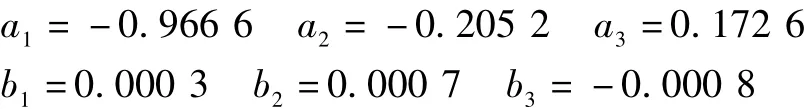
系統的離散傳遞函數為
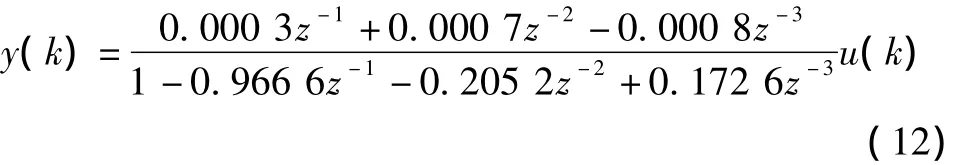
3.4 算法驗證及結果分析
如圖4所示,(a)為實驗得到的位移信號和由辨識模型計算得到的輸出信號的結果對比,(b)為誤差信號,可以看出誤差控制在0.03 V的范圍內。

圖4 算法驗證1
為了充分說明方法的有效性,對其進行了更進一步的驗證,改變輸入白噪聲序列,將模型計算得到的輸出信號和實驗實際采集的液壓缸位移信號進行對比,如圖5所示。
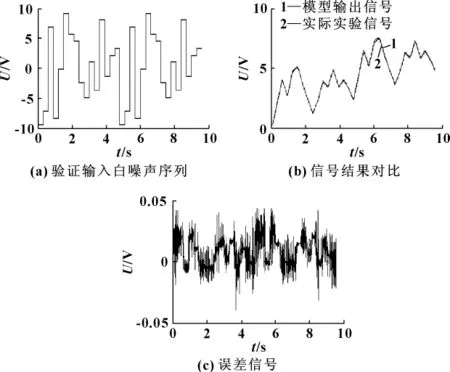
圖5 算法驗證2
通過對比模型輸出信號和實際實驗信號,證明辨識得到的模型是正確的,可以很好地反應輸出信號。
4 結論
閥控非對稱液壓缸的模型是一個三階系統,通過實驗采集了輸入輸出信號,并用基于梯度校正的參數辨識方法對模型的參數進行了辨識,最后進行了算法的驗證,證明此方法是可行的,為下一步建立導彈起豎液壓系統的模型和進行起豎控制奠定了基礎。
【1】呂云嵩.閥控非對稱缸頻域建模[J].機械工程學報,2007,43(9):122 -126.
【2】趙周禮,周恩濤,周士昌,等.非對稱缸系統精確建模方法研究[J].機床與液壓,2002(1):92-94.
【3】龐中華,崔紅.系統辨識與自適應控制MATLAB仿真[M].北京:北京航空航天大學出版社,2009.
【4】侯媛彬,汪梅.系統辨識及其MATLAB仿真[M].北京:科學出版社,2004.
【5】蔣威,高欽和,李天義.基于最小二乘法的比例閥建模和參數辨識[J].機床與液壓,2011,39(5):113 -114,124.
【6】倪博溢,蕭德云.MATLAB環境下的系統辨識仿真工具箱[J].系統仿真學報,2006,18(6):1493 -1496.

