基于小波變換和GM-ARMA的導彈備件消耗預測

趙建忠 徐廷學

(海軍航空工程學院兵器科學與技術系，煙臺 264001)

葛先軍 尹延濤

(海軍航空工程學院科研部，煙臺 264001)

備件是進行導彈裝備使用和實施維修等保障任務的重要物質基礎，準確地預測備件的消耗才能在有限的經費情況下，最大限度地滿足導彈裝備保障的備件需求.在備件預測領域，時間序列分析由于避免了影響因素調查與篩選、多重共線性等難點而得到廣泛應用.導彈備件消耗大都呈現“短周期、小樣本”的特點，這表明依靠大樣本數據進行建模的方法來預測導彈備件的消耗，很難達到預期效果.灰色模型(GM，Grey Model)是建立系統運行趨勢模型的有效方法，適用于動態預測，且只需知道少量已知信息就可建立預測模型.另外，自回歸移動平均模型 (ARMA，Autoregressive and Moving Average)，是分析平穩隨機信號的一種成熟而有效的方法，能處理周期性變化的序列，且建模時所需數據量少.由于2種模型對于時間序列的預測各有側重，一些學者提出了GMARMA組合模型(grey model and autoregressive integrated moving average model)［1］.但子模型 GM(1，1)模型對波動大、非線性、非平穩的序列難以取得滿意的預測效果，而數據變換技術為建立灰色模型創造先決條件;ARMA模型參數的估計過程是復雜的非線性回歸過程，導致ARMA模型參數估計成為模型運用的一個難點，而阻尼最小二乘法為其提供了一條有效的途徑.為此本文提出了改進的GM-ARMA模型以克服上述缺點，稱為RGM-ARMA模型(revised GM-ARMA).

導彈備件消耗大都呈現非線性、非平穩特征，導致利用RGM-ARMA模型進行導彈備件消耗預測誤差仍偏大.小波變換是近年來興起的一種新的信號分析處理技術，具有多分辨分析的特點，在時域、頻域都具有表征信號局部特征的能力，是處理非平穩隨機時間序列的一種有效方法［2］.目前，小波變換技術廣泛應用于信號處理、圖像處理、計算機視覺等領域，但被用于備件預測方面的研究還幾乎沒有.為了解決備件消耗預測問題，本文嘗試將小波變換技術引入到備件消耗預測領域.

至此，在分析導彈備件消耗特性以及備件消耗預測模型研究現狀的基礎上，提出一種基于小波變換和RGM-ARMA的導彈備件消耗組合預測方法，稱為 WGM-ARMA模型(wavelet transform，revised grey model and autoregressive integrated moving average model).在充分擬合低頻信息的同時，又避免對高頻信息的過擬合，從而提高了非平穩時間序列的預測精度，為備件消耗預測提供了一種新的思路.

1 小波變換理論

小波變換有很多算法，常用的有快速變換算法:Mallat算法和A Trous算法等.本文根據備件消耗序列長度，采用Mallat算法，即塔式算法.該算法從空間概念方面形象地說明了多分辨分析特性，并給出了信號分解不同頻率通道的算法及重構算法［3］.

2 GM-ARMA模型的改進

2.1 基于背景值優化和數據變換技術的改進GM(1，1)

2.1.1 振蕩序列的改進

文獻［4－5］論證了平移變換可以使任意的原始數據序列X變為一個單調遞增的序列X1;文獻［6－7］幾何平均變換不但可使序列X1的隨機波動性減弱，消除沖擊干擾項對系統造成的數據“失真”現象，而且還能保持原有數據序列X1的單調性，并提高序列X1的光滑性.因此，通過對平移變換和幾何平均變換后生成得到的數據序列建立GM(1，1)模型，可以有效地提高預測模型的模擬精度.

2.1.2 背景值的優化

設 X={x(1)，x(2)，…，x(n)}為原始時間序列，計算背景值 Z(1)時，Z(1)(i)=θx(1)(i－1)+(1 － θ)x(1)(i)(i=1，2，…，n).其中，X(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}為原始數據序列的一次累加序列，θ為(0，1)之間的待定常數.

2.1.3 模型的建立

先對X進行平移變換，得到的序列記作

其中，x1(k)=x(k)d1，k=1，2，…，n;然后對 X1進行幾何平均變換，生成的序列記作

其中，y(k)=x1(k)d2，再以 Y={y(1)，y(2)，…，y(n)}為原始序列建立GM(1，1)微分方程.求解并作一次累減生成得

2.2 基于阻尼最小二乘法優化的ARMA

本文利用反向過程確定數據初值，結合阻尼最小二乘法，求解ARMA模型的參數［8－9］.

條件最小二乘法中的條件是指初值條件［10］，當一時間序列用ARMA模型來擬合，假設此序列中第一個時刻之前的p個時刻的值為0或者均值，相對應的殘差序列的前q個時刻的值為0.

首先用反向過程確定初值，假設時間序列x1，x2，…，xn，需要去估計 x－i(i=1，2，…，n)，可以由反向模型所產生算子:φ(F)xk=θ(F)φk.

由于該算子的平穩性，在一定的范圍k=ε以外，估計值基本上等于0［11］.因此，對充分的近似值，用式(4)來求解.

將混合過程用一個ε階滑動平均過程代替.接著將模型線性化，而且要極小化

將［φk］用 Taylor級數展開，m=p+q個參數用β作為(φ，θ)的記號，在該值附近有一組推測的對應參數值 β0=(β1，0，β2，0，…，βm，0)，則有

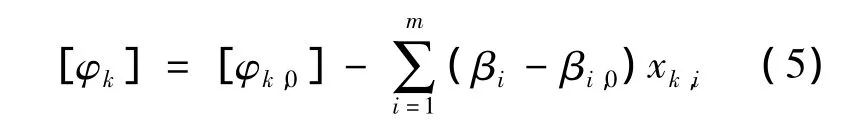
再使用阻尼最小二乘法進行計算，阻尼最小二乘法是Newton法與最速下降法的結合，不僅收斂速度快，而且精度高［12－13］.

對于給定的模型，值［φm|x，β1，0，β2，0，…，βm，0］對于 k=1 － ε，…，n 用遞推方法，然后對［φm|x，β1，0+ δ1，β2，0，…，βm，0］重復遞推計算，繼而又對［φm|x，β1，0，β2，0+ δ2，…，βm，0］進行遞推 計算，由

可得到具有足夠精度的所需導數負值，求取［φk］，最后計算出預期的ARMA模型參數.

3 WGM-ARMA模型的構建

在上述分析和研究的基礎上，對導彈備件消耗預測的思路和框架進行規劃.首先對備件消耗序列進行分解與重構，然后對低頻和高頻信息分別建模和預測，最后將各個預測結果進行疊加，便得到原始序列的預測結果.預測框架見圖1.

圖1 基于WGM-ARMA的導彈備件消耗預測框架圖

在WGM-ARMA模型中，需要整合3種模型，這里模型的整合優化是建立WGM-ARMA模型的關鍵.首先要對小波基和分解層數進行參數化:參數m代表小波基，參數k代表分解層數.在灰色模型GM(1，1)中的特征參數是θ，在ARMA模型特征參數是(p，q)，在小波分解的特征參數是(m，k)，而整合GM(1，1)，ARMA模型和小波分解的過程就是找到特征參數組合(θ，p，q，m，k)最佳組合的過程.建立組合模型基本的前提條件是θ，(p，q)和(m，k)的選擇必須基于相同的統計準則［14］.顯然參數(m，k)可以用總絕對值誤差(TAE，Total Absolute Error)準則［15］選擇，因此模型的整合可以依據TAE準則進行選擇.

對于給定的時間序列 X=(x1，x2，…，xn)，已知小波基方程m和小波分解的層數k，根據小波分解，該時間序列X可以被分解為

對參數(m，k，θ，p1，q1，p2，q2，…，pk，qk)設定上下限，得到一個離散的參數空間:

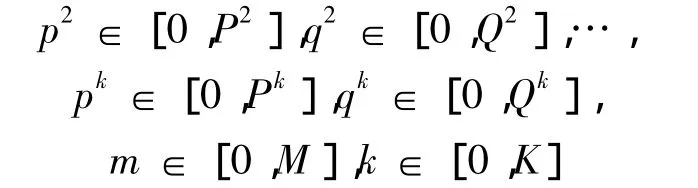
這樣對于參數組合(m，k，θ，p1，q1，p2，q2，…，pk，qk)，通過式(7)計算出擬合序列 X=(x^1，x^2，…，x^n)，并計算出對應的總絕對值誤差為

而最終的WGM-ARMA模型滿足:

4 實例分析

據調研分析，某型導彈裝備的使用和維修保障過程中，由于電流電壓不穩或電子器件到壽、振動或沖擊、橡膠老化或受力等因素，導致導彈裝備出現電子件短路斷路或擊穿燒蝕、機械件斷裂或磨損、橡膠件斷裂或磨損等現象，進而導致相應備件的消耗.這里統計了該型導彈裝備某種備件1998年－2010年的消耗情況(見表1).

表1 1998年－2010年某種導彈備件的消耗數據

4.1 數據分析

由表1知，備件消耗序列是非平穩的時間序列，先采用小波分析理論把備件消耗序列進行分解和重構.這里數據樣本共13組，選取前10組數據樣本構建模型，擬合模型;后3組數據樣本用來作為預測值的比較對象，以檢驗預測效果的好壞.

4.2 消耗預測

4.2.1 參數確定

首先對參數(m，k，θ，p1，q1，p2，q2，…，pk，qk)設定上下限.對參數m進行編號，如表2所示.經研究比較，對參數(k，θ，p1，q1，p2，q2，…，pk，qk)定義的上下界為 k∈［1，2，…，6］，θ∈［0，0.1，…，1］，p1，q1，p2，q2，…，pk，qk∈［0，1，…，5］.到此，對于每個參數組合(m，k，θ，p1，q1，p2，q2，…，pk，qk)都可以基于10個歷史數據X=(x1，x2，…，x10)通過式(7)建立模型，并得到擬合序列X^，并通過式(8)計算出相應的σTAE，且WGM-ARMA模型滿足式(9).

上述式(7)～式(9)的計算過程可以用Matlab編程實現，最終計算出來的σTAE最小的參數組合為:m=4，k=2，θ=0.6，p1=2，q1=1，p2=2，q2=2.根據第3節參數定義和表2可知，m=4表明首先要用小波基方程“db3”，k=2表明通過小波分解把原始序列X分解2層，低頻逼近信號、高頻細節信號和重構信號見圖2.

表2 小波基方程的編號

圖2 備件消耗時間序列及用db3小波分解后重構結果

由于db N小波具有正交、時頻支撐、高正規性和Mallat快速算法等特點，對非平穩時間序列的分解具有很好的特性，但消失矩不能太高，一般不超過4，即db2～db4比較合適;分解過程中本身存在計算誤差，層數越多，誤差越大，計算上的誤差會帶來預測的誤差，使預測精度下降，一般為2～5層［16］.由此可見，在分解過程中小波基和分解層數的選擇是比較合理的.

4.2.2 低頻逼近信號預測

對小波分解后的低頻逼近信號采用改進GM(1，1)模型(θ=0.6)進行預測，數據擬合情況如圖3所示.后驗差比值 C=0.032＜0.35，小誤差概率P=1＞0.95，預測模型等級為優，可以用于低頻逼近信號預測.

4.2.3 高頻細節信號預測

對小波分解后的高頻信號采用ARMA模型(p1=2，q1=1，p2=2，q2=2)進行預測，數據擬合情況及其誤差相關系數如圖4和圖5所示.由此可見，ARMA模型的預測信號值和原始信號很接近，預測精度較高，可以用于高頻細節信號的預測.

圖3 低頻信號的灰色擬合效果

圖4 高頻信號1的ARMA擬合及其誤差相關系數

圖5 高頻信號2的ARMA擬合及其誤差相關系數

4.3 結果分析

在上述分析的基礎上，把低頻逼近信號和各層高頻細節信號在第11～13時間點的預測值相加，便得到2008年－2010年的備件消耗量.作為對比，再采用傳統的 GM(1，1)、改進的 GM(1，1)、ARMA模型、RGM-ARMA模型，分別對備件消耗進行預測，這5種方法的預測結果如圖6所示，平均相對誤差(MRE，Mean Relative Error)分別是0.0622，0.0465，0.0497，0.0344，0.0152.

圖6 預測誤差對比

5 結 束 語

本文嘗試把小波變換引入到導彈備件消耗預測中，提出了基于小波變換和改進GM-ARMA的導彈備件消耗預測方法，其顯著特點是運用小波變換技術將非平穩的備件消耗時間序列分解為多層頻率成分更加單純、相關性更強的序列，并且針對各層的特點，用改進的GM(1，1)和ARMA模型分別對分解后的非線性低頻趨勢信息和相對平穩高頻信息進行預測，疊加各子序列的最終預測效果優于單一預測模型.更為重要的是，本文提出了一個基于小波變換的全新的構建組合預測模型的思路，進而構建出更多更精確的備件預測模型.研究結果表明，基于小波變換的多種模型相結合的方法，不僅能夠反映原始備件消耗數據的結構特征及變化規律，而且還可以發揮各模型的優勢，取得了較高的預測精度且預測性能穩定，對進一步解決實際問題具有良好的應用前景.

References)

［1］胡效雷，何祖威.基于GM-ARMA組合模型的年電力需求預測［J］.廣東電力，2007，20(2):10 －13 Hu Xiaolei，He Zuwei.Forecasting about annual electric consumption based on GM-ARMA combined model［J］.Guangdong Electric Power，2007，20(2):10 －13(in Chinese)

［2］ Amjady N，Keynia F.Short-term load forecasting of power systems by combination of wavelet transform and neuro-evolutionary algorithm［J］.Energy，2009(34):46 －57

［3］馬林才，許瑋瓏，劉大學.基于小波變換的城市市區典型路段交通流量預測［J］.控制與決策，2011，26(5):789 －793 Ma Lincai，Xu Weilong，Liu Daxue.Prediction model of traffic flow along typical roads in city urban district based on wavelet transform［J］.Control and Decision，2011，26(5):789 －793(in Chinese)

［4］錢吳永，黨耀國.基于振蕩序列的GM(1，1)模型［J］.系統工程理論與實踐，2009，29(3):149 －154 Qian Wuyong，Dang Yaoguo.GM(1，1)model of oscillation sequences［J］.Systems Engineering Theory ＆ Practice，2009，29(3):149－154(in Chinese)

［5］ Bo L，Yong W.Optimized GM(1，1)grey model based on connotation expression［J］.Journal of Grey System，2007(3):133－136

［6］趙宇哲，武春友.灰色振蕩序列GM(1，1)模型及在城市用水中的應用［J］.運籌與管理，2010，19(5):155 －166 Zhao Yuzhe，Wu Chunyou.GM(1，1)model of grey oscillation sequences and its application to urban water consumption forecasting［J］.Oerations Research and Management Science，2010，19(5):155－166(in Chinese)

［7］ Wang M H.Grey-extension method for incipient fault forecasting of oil-immersed power transformer［J］.Electric Power Component and Systems，2004，32(10):959 －975

［8］ Ives A，Abbott K C，Ziebarth N L.Analysis of ecological time series with ARMA(p，q)model［J］.Ecology，2010，91(3):858－871

［9］ Carden E P，Brownjohn JMW.ARMA modeled time-series classification for structural health monitoring of civil infrastructure［J］.Mechanical Systems and Signal Processing，2008，22(2):295－314

［10］ Topres JL，Garcl A，Deblas M，et al.Forecast of hourly average wind speed with ARMA models in Navarre［J］.Solar Energy，2005(79):65－77

［11］ Kim H J，Shin K S.A hybrid approach based on neural networks and genetic algorithms for detecting temporal patterns in stock markets［J］.Applied Soft Computing，2007，7(2):569 －576

［12］ Bermudez JD，Segura JV.A decision support system methodology for forecasting of time series based on soft computing［J］.Computational Statistics ＆ Data Analysis，2006，51(1):177－191

［13］ 何永沛.ARMA模型參數估計算法改進及在股票預測中的應用［J］.重慶工學院學報:自然科學版，2009，23(2):109 －112 He Yongpei.Improved algorithm of parameter estimating for ARMA model and its application in the stock markets forecasting［J］.Journal of Chongqing Institute of Technology:Natural Science，2009，23(2):109 －112(in Chinese)

［14］吳朝陽.改進的灰色模型與ARMA模型的股指預測［J］.智能系統學報，2010，5(3):277 －281 Wu Zhaoyang.Forecasting stock index based on revised grey model and ARMA model［J］.CAAI Transactions on Intelligent Systems，2010，5(3):277 －281(in Chinese)

［15］吳朝陽.小波變換和GM-ARMA組合模型的股指預測［J］.智能系統學報，2011，6(3):279 －282 Wu Zhaoyang.Using wavelet transformation and a GM-ARMA model to forecast stock index［J］.CAAI Transactions on Intelligent Systems，2011，6(3):279 － 282(in Chinese)

［16］李持佳，焦文玲，趙林波.燃氣短期負荷預測的小波分析綜合模型［J］.天然氣工業，2007，27(8):103 Li Chijia，Jiao Wenling，Zhao Linbo.A synthesis wavelet analysis method for short-term gas load prediction［J］.Natural Gas Industry，2007，27(8):103(in Chinese)