基于NURBS曲線的新型插補技術
唐良寶,祖重光
(桂林電子科技大學,廣西桂林541004)
目前,在CAD /CAM系統中,參數形式的自由曲線曲面已經成為描述零件外形輪廓的最常用的數學方法之一[1]。NURBS曲線因具有良好的局部控制和形狀表達能力,以及能夠對解析曲線和自由曲線進行精確的統一表達,已成為STEP-NC 標準中自由曲線曲面的標準表達形式。并于1991年被國際標準化組織(ISO)規定為工業產品模型數據交換標準,該標準是定義工業產品幾何形狀的唯一標準[1]。
時間分割法是NURBS曲線常用的數據采樣插補方法,基本原理是按照插補周期進給段的長度來分割曲線,以弦線來逼近待插補曲線。NURBS曲線插補一般分為粗插補和精插補兩個部分。其中在粗插補部分,依據加工機械的進給速度和加工件的精度要求等因素,對曲線進行插補運算確定插補點,這是NURBS曲線插補的主要任務。粗插補的目的是獲得加工所需要的微小直線段并建立合理的加工速度,使得加工曲線更為平滑。精插補部分則可以根據現有的直線或圓弧插補技術來進行加工。
1 NURBS曲線的數學模型[2]
一條NURBS曲線可以表示為一分段有理多項式矢函數:
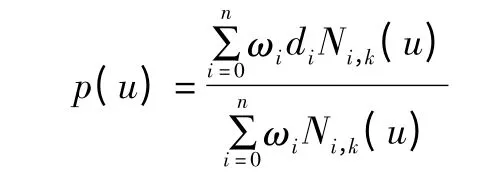
其中:ωi(i=0,1,…,n)稱為權因子,分別與控制定點di(i=1,2,…,n)相聯系。首末權因子ω0,ωn≥0,且順序k個權因子不同時為零,以防止分母為零、保留凸包性質及曲線不致因權因子而退化為一點。Ni,k(u)是由節點矢量U=[u0,u1,…un+k+1]決定的k次規范B 樣條基函數。
2 TAYLOR 公式展開法求NURBS曲線插補點
由于精確的NURBS曲線反函數難以準確地獲得,并且在插補過程中通常是以直線逼近曲線的,因此,在求輪廓步長和對應關系時多采用數值方法近似求取。在NURBS曲線插補中常用的方法是TAYLOR展開法。
在NURBS曲線插補中,為了便于計算、縮小計算量,通常采用一階或二階精度。因此,ui+1可表示為:
一階近似式:

二階近似式:
使用TAYLOR方法,在確定了插補周期之后,在計算NURBS曲線上下一個插補點時,需要進行速度規劃,并且進行反求ui+1計算和p(ui+1)求解計算。由于在反求ui+1時,涉及到求p(u)的一階導數甚至是二階導數,計算量大不利于實時插補。另外在高曲率階段,使用TAYLOR展開法速度波動大,在機械系統驅動能力不能滿足要求時,使用TAYLOR展開法會產生較大的誤差。
3 二分預估校正法
采用預估校正法求解確定插補周期下NURBS曲線上的點,可以將TAYLOR展開法的兩個步驟合并起來。直接運用正向運算,避免了NURBS曲線的求導運算。二分預估校正法可以分為兩個部分,即插補點預估和校正兩個階段。圖1為預估校正算法的基本流程圖。
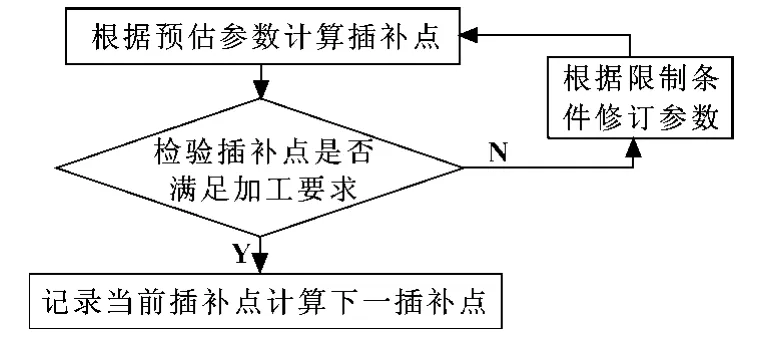
圖1 預估校正算法的基本流程圖
二分預估校正法的計算過程。假設當前的插補點所對應的參數值為ui,經過一個插補周期T 后,下一個插補點所對應的參數值為ui+1。采用二分預估校正法時,ui+1可由公式ui+1=ui+Δui直接預估獲得,這里Δui=ui-ui-1為前一個插補點的參數增量。應用de Boor 遞推公式[2]計算相對應的NURBS曲線上的點p(ui+1)。計算點p(ui)與p(ui+1)之間的弦長值Δsi+1,比較Δsi+1與標準步長Δs之間的誤差是否滿足許用精度,進而確定曲線插補點p(ui+1)和參數值ui+1。圖2所示為二分預估校正法的計算流程。
4 曲線弓高誤差的計算
在應用二分預估校正法計算NURBS曲線時,曲線上各個插補點之間的弧長是由弦長近似代替的,因此在曲線弧和弦線之間存在著弓高誤差,如圖3所示。線段AB 即為曲線的弓高誤差δ。傳統的計算弓高誤差的方法是應用公式得出,但當曲線為自由曲線時曲率半徑ρ的計算非常復雜。
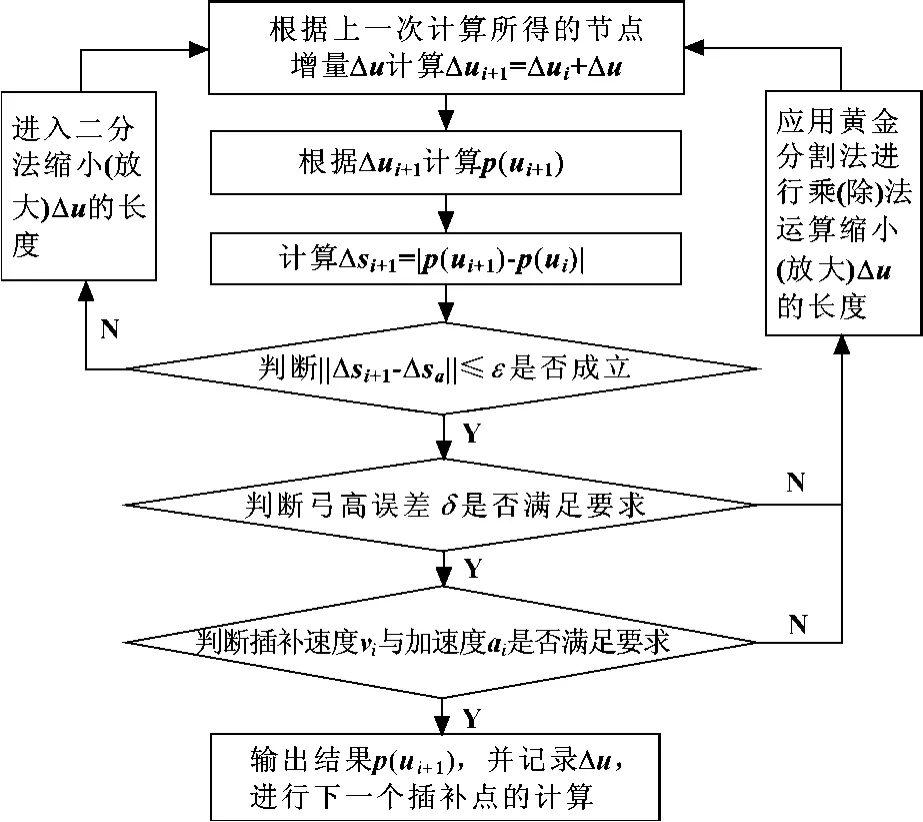
圖2 二分預估校正法的計算流程
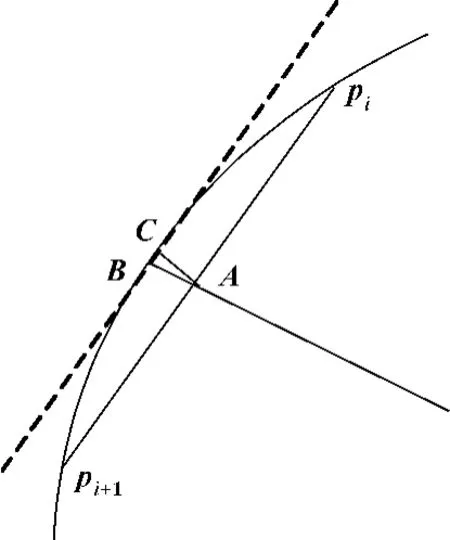
圖3 弓高誤差圖
由于在NURBS曲線插補過程中每個插補周期T(ms)的進給量非常微小,在給定的加工速度下曲線的插補增量也非常微小,因此擬用近似直線段AC 代替曲線弓高誤差AB,其中點C為曲線上點點A坐標為由此得線段AC的長度計算公式為此即為弓高誤差δ的近似計算公式。
5 進給速度自適應控制
為了不使插補計算過程中產生超出加工設備驅動加工能力的速度指令,需要對曲線進行插補周期內速度與加速度檢驗。

這樣求得的插補軌跡便具有了進給速度自適應的能力,并且將進給速度和進給加速度控制在給定的范圍之內。
6 實例計算
被插補的3次NURBS曲線如圖4所示。采用二分預估校正算法對曲線進行插補仿真運算,程序在Visual C++6.0 環境中運行,插補周期T=0.002 s,最大弓高誤差δ=0.001 mm,最大軸向速度vmax=200 mm/s,最大軸向加速度amax=500 mm/s2。圖5給出了計算過程中Δu與Δs之間的關系。

圖4 3次NURBS曲線

圖5 實例曲線Δu與Δs之間的關系
從圖5可以看出:在高曲率部分 (圖中圓圈A中所示部分),參數增量Δu 和位移增量Δs之間是單調遞增關系,位移偏差可以通過改變參數增量的大小來實現;并且當參數增量變化很小時,位移增量近似等于參數增量。另外結合圖4可以看出:在曲線曲率較平緩的區域,位移增量也基本趨于不變。
采用插補點預估校正算法避免了對NURBS曲線求導運算,簡化了計算過程。表1給出了相同插補周期(T=2 ms)下TAYLOR展開法與二分法的插補計算時間。

表1 計算時間對照表(插補周期T=2 ms)次/ms
7 總結
NURBS曲線插補技術是高性能CNC系統的標志之一。在開放式數控系統中,引入NURBS曲線插補技術能夠有效地提高插補速度和插補精度。NURBS曲線的插補點計算過程的簡化,能夠有效地提高插補計算效率,使插補運算更適用于實時控制。文中用二分法預估校正算法代替傳統的TAYLOR展開法進行插補計算,簡化了插補過程,提高了插補計算的效率。
【1】吳穎輝,諶永祥,李永橋.NURBS曲線插補技術在CNC中的應用[J].信息技術,2011,40(2):94-96.
【2】施法中.計算機輔助幾何設計與非均勻有理B 樣條[M].北京:高等教育出版社,2001:306-343.
【3】滕二,桂貴生.NURBS曲線插補在高速加工中的應用[J].組合機床與自動化加工技術,2009(8):26-28.
【4】和廣強,于東,張曉輝.基于速度前瞻控制的五軸NURBS曲線插補方法[J].組合機床與自動化加工技術,2011(5):38-45.
【5】郝雙暉,宋芳,金立川,等.同周期控制NURBS曲線高速高精度插補算法研究[J].機械設計與制造,2010(7):12-14.
【6】馬方魁,郇極.數控機床NURBS曲線插補運動誤差分析與仿真[J].中國機械工程,2008,19(20):2446-2449.
【7】楊旭靜,胡仲勛,鐘志華.面向刀具路徑生成的NURBS曲線擬合算法研究[J].中國機械工程,2009,20(8):984-987.
【8】宋春華.數控技術的現狀及發展趨勢[J].裝備制造技術,2011,30(3):40-42.
【9】沈洪奎.自適應NURBS曲線插補關鍵技術及實現研究[D].杭州:浙江大學,2010.
【10】劉宇,戴麗,劉杰.泰勒展開NURBS曲線插補算法[J].東北大學學報,2009,30(1):117-120.
【11】LEI W T,SUNG M P,LIN L Y,et al.Fast Real-time NURBS Path Interpolation for CNC Machine Tools[J].International Journal of Machine Tools & Manufacture,2007,47:1-12.

