淺談煙塵采樣的兩種分析驗證方案

趙佳

（廣州鐵路疾病預防與控制中心 廣東廣州510080）

本文應用污染物傳遞數學模型驗證煙塵采樣器的采樣效率和準確度。污染物傳遞分析主要包含兩個首要任務，其一是明確污染物傳遞的途徑并深入解析該途徑中物理、化學、生物的污染轉換程度；其二是將這些途徑合并為數學概念，以至于可計算的式子、電腦模型，可用于評估和計算空氣、食物和水中的污染。在本案中污染物為煙塵顆粒物，其傳遞途徑主要通過氣體物理輸送，過程當中的化學和生物降解過程在第一種方案中忽略不計，而在第二種方案中則依照一次降解的方法計算其降解速率。

本案中在給出了兩種數學方案，第一種方案首先應用了物質守恒定律確定和表示煙塵在采樣器中的濃度，然后假設煙塵在采樣器接口位置之后經過一段物理運動重新達到采樣前煙道內的煙塵濃度，從而得到采樣后煙塵濃度和采樣器內濃度的數學關系，由此推導出煙道面積和采樣時間以及煙塵通量Q 之間的數學等式，因此可以判斷煙塵采樣器的采樣效率。

第二種方案在第一種的模型基礎之上給出在給定的時間，污染物移動距離的前提下煙塵濃度C(x,t)隨x，t 的變化而變化的數學模型。對偏微分方程兩邊進行拉普拉斯變換，由初始條件C(x,0)=C 可得對t 進行拉普拉斯變換后的含有的微分方程，再由初始條件C(0,s)=C 對x 進行拉普拉斯變換得到含有的方程，因此得到并對其進行拉普拉斯逆變換，最后可得在給定的時間t，污染物移動距離x 的前提下煙塵濃度C(x，t)。

方案一 如下圖1 中所示，煙道內初始有質量為S(Kg)煙塵進入，經采樣口采樣后剩余質量S1(Kg)煙塵；煙塵管道截面積為A，在t 時間內，煙塵經采樣口位置運動距離為x(m)，則煙塵濃度為C(x,t)。假設管內煙塵分布均勻且保持勻速單向運動，由質量守恒規則可知

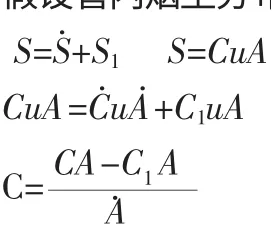
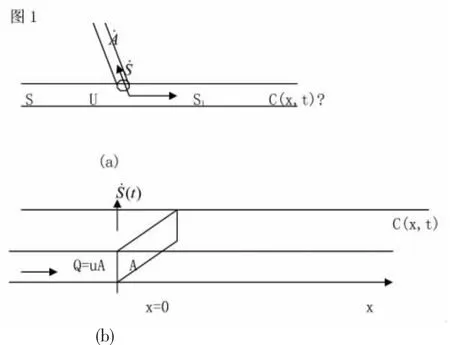
1.1

從x=0 開始至某一時間t，煙塵在采樣口減少了一定質量后經過一段時間的物理運動重新達到均勻分布且勻速運動，這個過程可以看做經過了一個持續攪拌運動的反應容器(Continuousflowstirred tank reactor)。當進入該容器和離開容器的氣體通量為Q（L3/T）=uA，進入容器的污染物濃度為C1，容器的體積為V 是常量，可以得到關于濃度C(t)的微分方程。

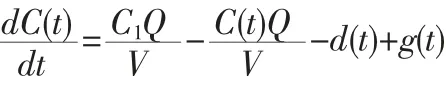
d(t)表示t 時間內煙塵降解速率，g(t)表示新煙塵產生的速率。在這里g(t)表示的化學和生物過程產生的新煙塵忽略不計，則上式中

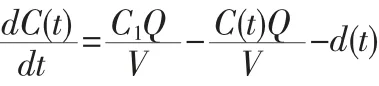
假設降解速率為一次降解率，則表示為

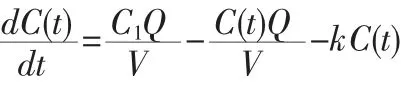
1.2

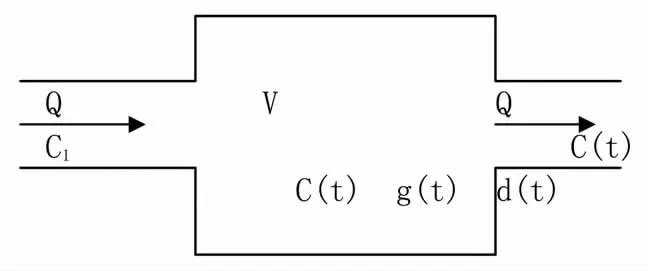
圖2

解此微分方程得到

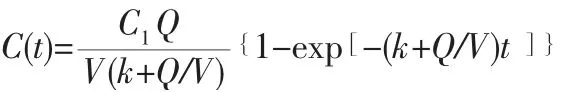
1.3

當 將其代入式子1.1 得到

1.4

再將1.3 代入可得到C 關于C1的函數。若已知降解速率k，由儀器測定的氣體輸送速率u，可得t 時間內的氣體通量Q，以及假定容器容量V，因此代入1.4 中可得到C 關于C1的函數C=KC1。

當C 與C(t)接近，C≈C(t)可得

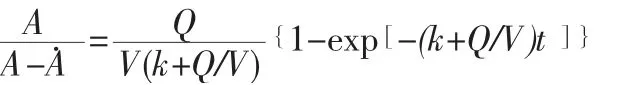
1.5

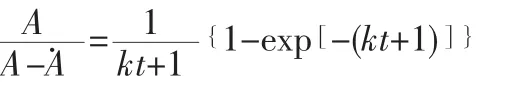
1.6

方案二該方案是基于第一種方案模型的偏微分數學推導式子（2.1）得出在給定的時間t，污染物移動距離的前提下煙塵濃度C(x,t)隨，的變化而變化的數學模型。其中偏微分推導式(2.1)中D 是污染物擴散系數，該項代表污染物在平行于方向的平面上的污染物擴散速率，假設污染物降解率為一次降解即。

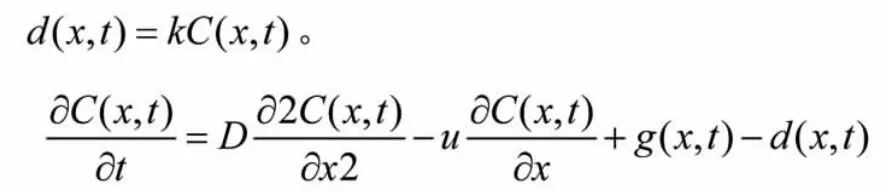
2.1

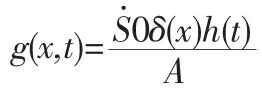
g(x,t)表示采樣器吸入污染物后煙道內煙塵濃度的變化情況。其中方案一當中的S 由上式中S0替代。（2.1）簡化后的單方向一次降解率數學表示式子如下：

2.2

對2.2 該偏微分方程做拉普拉斯變換得

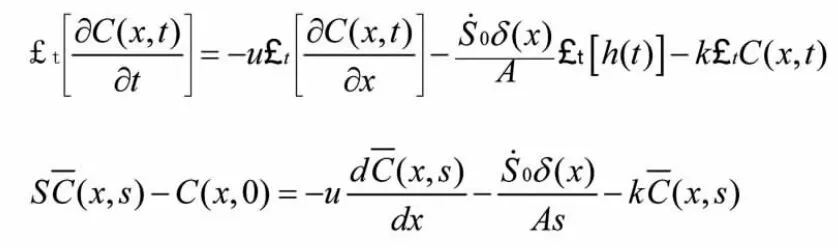
初始狀態下C(x,0)為假設已知或可測污染物濃度，則

2.3

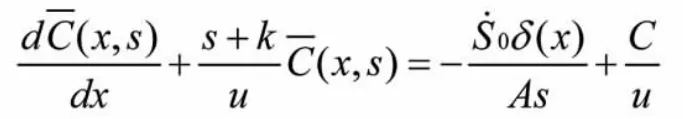
再對以上微分方程進行拉普拉斯變換，可得

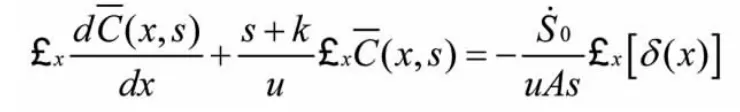
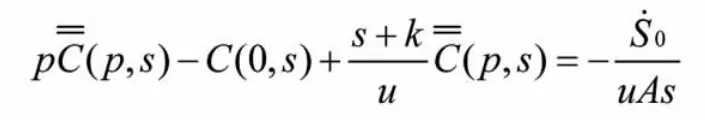
初始狀態下

C(0,s)=C

則可得

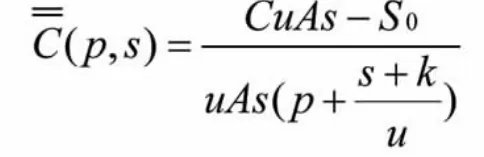
對上式進行拉普拉斯逆變換

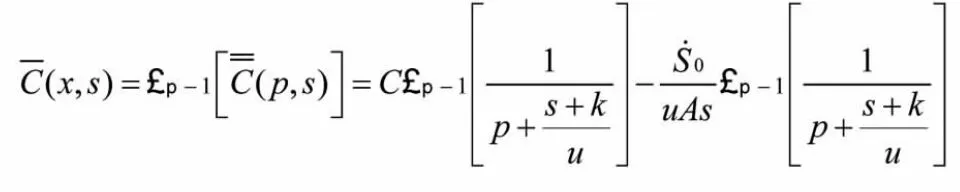
由已知拉普拉斯變換公式推導

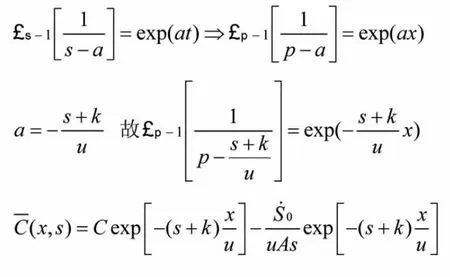
對上式子再做拉普拉斯逆變換得

2.4

由拉普拉斯逆變換公式

其中a=x/u，

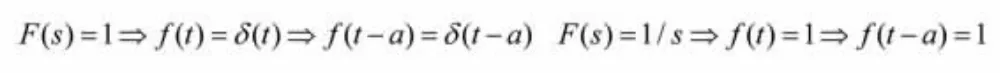
代入2.3 得

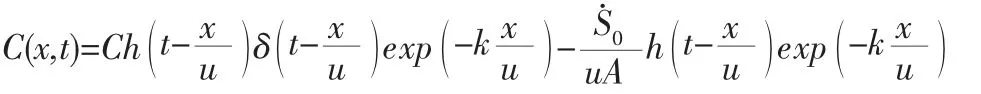
2.5

根據（2.3）得求得在給定的時間t，污染物移動距離x 的前提下煙塵濃度隨x，t 的變化的值。由此可確認時間下煙塵采樣器的采樣效率。

3 結論

我們可運用以上兩種方案到實踐中驗證煙塵采樣器的采樣效率以及準確度。方案一由式子1.5 可得由采樣時間，一次降解速率k 與采樣面積A，煙道面積A 之間的數學關系，并假定容器容量V=uAt，容器氣體通量Q=uA 推得式子1.6，因此求出達到平衡所需的采樣時間t。并且可以由此推斷在已知的t 時間下，采樣效率是否已達到理想的狀態。方案二當中引入了污染物移動距離x和給定時間t，由拉普拉斯方程逆變換得出給定時間t，污染物移動距離為x 條件下的煙塵濃度，由此可知在一定的采樣時間條件之下，煙塵濃度隨采樣時間的變化規律，并由此得到多長時間下采樣的效率得以最大化。

小米粒的綠色生活