基于約束誤差判據的動態地形可視化算法

于 萍， 張彩明

（1. 淄博師范高等專科學校信息科學系，山東 淄博 255130；2. 山東大學計算機科學與技術學院，山東 濟南 250101）

地形可視化是是虛擬地理環境中不可缺少的組成部分，目前國內外研究地形繪制主要基于層次細節（Level of Detail, LOD）模型技術。但在已有的大多數LOD算法[1-3]中，均隱含著一個相同的假設條件，即假定地形表面各處的高程值和顏色等物理屬性，在系統運行過程中是固定不變的。然而汽車等運載工具在松軟的地表上行駛會留下清晰的輪胎印跡、炸彈在地面上爆炸會產生彈坑。像這種地形表面各處的高程值和顏色等物理屬性在系統運行過程中不斷變化的動態地形并不滿足假設條件。并且動態地形的實時可視化對構建高逼真度的仿真環境具有重大的現實意義，也是視景仿真領域必須解決的重大問題。

利用LOD繪制大規模地形主要考慮3方面技術：數據組織方式，方便LOD模型生成并避免T-連接和裂縫的產生；誤差判據，減少每幀需要繪制的三角形數目提高算法效率并保證地形有較強的真實感；性能優化，幀間連貫性、視錐剔除、三角形條帶化等技術優化算法性能提高算法效率。其中，誤差判據決定了當前視點下，不同分辨率的地形模型需要繪制的三角形結點。因此，誤差判據決定著每幀需要繪制的三角形結點個數，取值的大小直接決定著渲染地形的真實度和算法效率，是LOD中的關鍵技術。對于動態地形，在地形發生動態形變（即地形的高程值和顏色等屬性發生變化）時，更希望通過誤差判據能較好的體現地形形變效果，增強形變地形的真實感。目前對于誤差判據的研究大致可以分為兩類。

一類是考慮視點因素[1-4]。與視點相關的誤差計算，常使用屏幕空間誤差方法。其主要有兩種方法：基于距離及視向的屏幕空間誤差計算法[5-6]和只基于距離的屏幕空間誤差計算法[4,7]。通過理論分析和實驗結果的對比指出：基于距離及視向的屏幕空間誤差計算法和只基于距離的屏幕空間誤差計算法，采用相同的屏幕誤差閾值對同一分辨率地表網格模型進行視點相關的簡化時，兩種簡化方法的簡化率相差不大。因此，只基于距離的屏幕空間誤差計算，因其計算簡單得到廣泛的應用[7-9]。

另一類考慮地形粗糙度因素[10-11]。地形粗糙度反映的是地形局部起伏劇烈程度的特征量，是較好的體現地形真實感的重要因素。對于較平坦的區域，可以用較低分辨率的三角網格表示；對于起伏較大的區域，需要用較高分辨率的三角網格表示。文獻[10]采用局部誤差計算方法，結點誤差由結點周圍5個結點的誤差和結點本身誤差的最大值表示，會有一定程度“跳躍”感的產生。文獻[11]提出的粗糙度計算方法需要從葉子頂點開始向上遞歸計算所有非葉子頂點的誤差，在地形發生動態形變時，也會增加算法的耗費時間，降低算法效率。

動態地形可視化需要在地形發生形變后能較好的體現地形局部形變效果，但又需滿足地形實時繪制的要求。為此，本文利用局部地形的粗糙度構造約束條件，加入視點因素后形成帶約束的嵌套誤差判據方法。不但可以很好地體現地形的形變效果，刻畫局部地形細節，還能隱式的避免T-連接和裂縫的產生，同時降低較平坦區域冗余三角形的產生。從而在保證動態地形有較強真實感的前提下，減少每幀中需要繪制的三角形結點個數，提高算法效率。

1 帶約束誤差判據的可視化算法

本文算法采用基于DAG的三角形二叉樹存儲結構，利用帶約束的誤差判據計算誤差，用較少的冗余三角形有效避免T-連接和裂縫的產生。同時利用延遲判斷的幀間連貫性，減少每幀的繪制時間提高算法效率。

1.1 基于DAG的三角形二叉樹

本文用三角形二叉樹[3,8,10]結構存儲需繪制的三角形信息。將初始平面的正方形區域劃分為兩個等腰直角三角形，并把他們定義為位于二叉樹的最頂層。對于頂層三角形，連接直角頂點和其斜邊的中點，三角形被平分為兩個子三角形，定義這兩個子三角形位于下一精細層，并稱頂層三角形為其父親。遞歸執行該操作，可生成層次結構的三角形二叉樹。在三角形二叉樹的構造過程中，實際上還隱含著嚴格的頂點引入次序。這種引入次序可用頂點的有向非循環圖DAG(Directed Acyclic Graph) 來描述。

1.2 帶約束的誤差判據

只基于距離的屏幕空間誤差計算，雖然計算簡單應用廣泛，但沒有考慮地形本身的起伏狀況。并且為避免T-連接和裂縫的產生，通常會增加冗余三角形。為此，利用局部地形的粗糙度，構造約束因子在體現地形本身起伏程度的同時降低冗余三角形個數。

1）約束因子

為了減少冗余三角形個數體現局部地形細節，利用地形粗糙度構造約束因子。考慮到動態地形運行中發生的形變，需要實時計算誤差函數，為減少實時計算量，本文提出基于方差的局部粗糙誤差函數。所謂局部粗糙度是指誤差中方差不是計算整個地形的方差，而是以結點為中心包含周圍結點的局部區域方差。主要考慮頂點附近局部區域的高程值對該頂點高程值的方差累計效果。取局部地形M×N，點i處構造局部粗糙誤差函數公式如下：

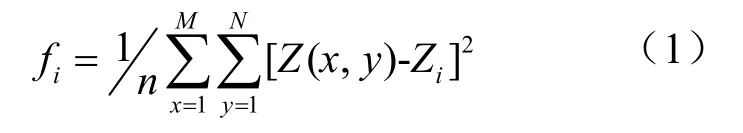
其中，Z(x,y)為局部地形頂點(x,y)的高程值，Zi為該頂點的高程值，n=M×N。利用局部粗糙誤差函數，構造值域在(0,1)區間內的頂點約束因子ki，具體計算公式如下：

若地形起伏較大，則fi的值較大，此時ki的值較大接近1。若地形較為平坦，則fi的值較小，此時ki的值較小。但地形平坦到接近平地時，會出現fi的值小于1，甚至為0的情況，此時ki的值反而較大，不能準確表示地形的粗糙程度。為此，在分母上修正fi為fi+1+ξ，以保證分母fi和ki的值不為0，其中ξ為接近0的極小數。如公式（3）所示。

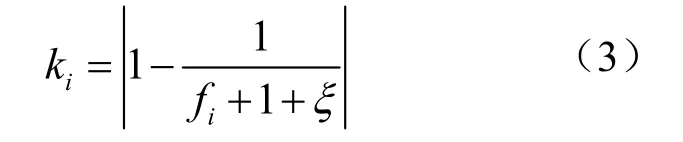
2）帶約束的誤差判據球

與視點相關的誤差計算考慮的是?ABC在引入斜邊AD后所產生的頂點空間誤差，用引入斜邊前后高程值差的絕對值表示δD=|ZD-(ZB+ZC) /2|。由此得到的只基于距離的屏幕空間誤差計算公式為：

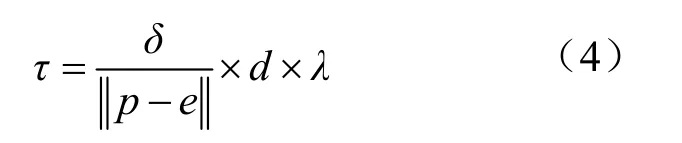
其中，λ表示對象空間中的單位長度，τ表示屏幕的空間誤差；p，e分別為結點、視點在三維對象空間中的位置；d為視點到屏幕平面的距離；δ表示與結點相對應的對象空間誤差。

在給定屏幕空間誤差閾值τ后，可以得到結點原始誤差判據球半徑為：

該式可看作在三維空間中以頂點i為球心,半徑為ri的球面, 稱之為頂點i的原始誤差據球。但 只基于視點考慮的誤差判據球沒有考慮地形局部粗糙程度，會產生一定的冗余三角形。為減少較平坦地區冗余三角形的產生，同時保留局部起伏較大區域的層次細節，利用地形局部粗糙度構造的約束因子ki約束誤差判據球。得到：

但利用帶約束的誤差判據球，在繪制地形時不可避免的會出現T-連接和裂縫。所謂T-連接是指一個三角形或多個三角形共享另一個三角形的一條邊的一部分。T-連接容易在繪制時產生地形裂縫，即使不產生裂縫，在繪制時T-連接出現的地方也會產生不連續的點，給人不真實的感覺。為此，利用嵌套誤差判據球將各個頂點間的包圍關系隱式的包含在誤差評價函數中，從而使所有需要分裂的子結點在繪制前其父結點早已分裂。因此，對與非葉子頂點需計算其嵌套誤差判據球，確保孩子頂點要求分裂時父結點都已經分裂。修改后頂點的帶約束嵌套誤差判據球，球心仍是該頂點的空間位置，半徑計算公式如下：

其中，ri為由式（6）所確定的頂點i的帶約束誤差判據球半徑，pi、pj分別為頂點i及其孩子頂點j的空間位置，Ci為DAG中頂點i的孩子集合，Rj為頂點j的嵌套誤差判據球半徑，稱式（7）所定義的誤差判據球為頂點的嵌套誤差判據球。

3）動態形變后的誤差計算

若地形在實時繪制階段發生動態性變，為盡可能的減少實時繪制中算法的計算量，本文采用與靜態地形不同的處理方法。給每個發生形變的頂點增加一位表示地形形變的標志位，當實時繪制中地形發生動態形變時，通過改變標志位狀態來確定發生形變的地形區域頂點。對形變區域的頂點重新計算其嵌套誤差判據球，并利用預處理時生成的DAG計算其祖先的嵌套誤差判據球。在計算形變區域的頂點的祖先嵌套誤差判據球時，并不需要計算所有的祖先結點，當重新計算的祖先結點的嵌套誤差判據球沒有改變時，即可停止其它祖先結點的誤差計算。

1.3 幀間連貫性

視點連續移動時，相鄰幀間地形的層次細節模型具有很大的連貫性，需繪制的三角形變化不大。因而利用幀間的連貫性[8-9]，對實時顯示的地形進行處理。從前一幀中顯示的三角形二叉樹的結點出發，根據當前視點的變化情況，判定下一幀需要繪制的結點。對視點離開其嵌套判定誤差球的頂點進行合并操作，對視點進入其嵌套判定誤差球的頂點進行分裂操作，對其它前一幀中顯示的頂點可直接顯示。考慮到ΔABC，如圖1所示，E表示視點位置，當E進入半徑為r的誤差判據球區域內時，ΔABC才需要分裂，當E離開半徑為R的誤差判據球區域時，ΔABC才需要合并。而當視點E在兩個誤差判據球間移動時，ΔABC無需進行視距與誤差判據球的判斷可直接顯示。因此，本文利用延遲因子，預測出頂點在當前視點移動速度下，最長延遲分裂或合并的次數。對上一幀中顯示的頂點，若其延遲因子遞減后非零則無需判斷可直接顯示。從而無需判斷上一幀中所有顯示的頂點，以減少實時繪制時的計算量，提高算法效率。若地形在實時繪制階段發生動態性變，除了重新計算形變區域的頂點嵌套誤差判據球外，還需重新計算形變區域各個頂點的延遲因子。并在計算后對形變區域的各個結點重新判斷，確定頂點是否需要判斷。

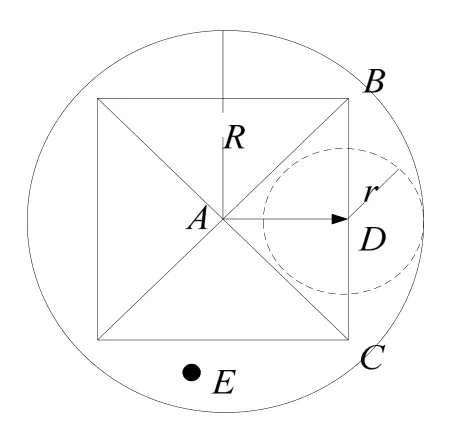
圖1 延遲示意圖

2 實現和分析

在PC機上實現了算法，并利用實驗地形數據進行了相關實驗。實驗硬件環境為：Intel P4 2.0GHz, 256M RAM, nVIDI2 A GeForce2 400 顯卡；軟件環境為：Windows 2000, VC6.0和OpenGL。

1）靜態地形誤差和效果圖比較

利用實驗地形數據[13]中的crater、island、maui 3個地形，分別對文獻[3]、文獻[11]和本文方法進行了比較。實驗中局部粗糙度因子取3×3局部地形高程值。對每個地形數據分別就其某視點下渲染的三角形個數和全局高程差進行了對比，如圖2、圖3所示。由圖2可以看出在地形渲染過程中本文算法所需繪制的三角形個數在多數情況下能明顯的低于文獻[3,11]。由圖3可以看出全局高程差3種計算方法相差不大。

圖2 3種地形下3種方法的三角形渲染個數對比

圖3 3種地形下3種方法的全局高程差對比

圖4 和圖5分別是某視點下，對較陡峭地形和較平坦地形的繪制效果圖，依次分別為全部三角形繪制，文獻[3]、文獻[11]和本文算法的比較，由圖4、圖5可以看出，雖然本文算法減少了繪制的三角形數目，但仍然能夠很好地體現地形地貌。

2）動態形變性能和效果比較

對地形發生動態形變的區域對比了文獻[11]和本文方法。圖6為文獻[11]和本文方法渲染的地形形變效果圖，由圖可以看出本文方法能很好的用較少的三角形繪制地形的形變效果。圖7比較了兩種方法在形變時的平均幀速、三角形個數和全局高程差，由圖可以看出本文方法在繪制時間和繪制三角形個數上明顯優于文獻 [11]，而全局高程差兩種方法差不多。

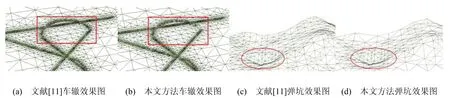
圖6 動態形變效果比較

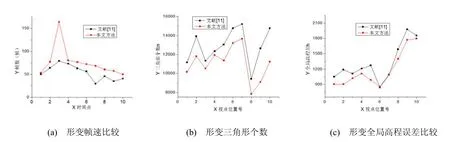
圖7 動態形變幀速、三角形個數和全局高程誤差比較

3 結 束 語

本文利用視點和地形本身粗糙因素，提出一種帶約束的誤差判據方法。該方法在隱式避免T-連接和裂縫生成的前提下，能有效地減少冗余的三角形結點個數，較好地提高算法效率，并且在地形發生形變時，能較好地體現地形的形變效果。實驗結果表明，該方法在保證地形有較強真實感的前提下，能很好地減少三角形個數，提高算法效率。

[1]Lindstrom P, Koller D, Ribarsky W, et al. Real-time continuous level of detail rendering of height Fields [C]//Proceedings of SIGGRAPH’96, New Orleans, 1996: 109-118.

[2]Hoppe H. Smooth view-dependent level-of-detail control and its application to terrain rendering [C]//Proceedings of IEEE Visualization’98, New Caledonia,1998: 135-142.

[3]Duchaineau M, Wolinsky M, Sigeri D E, et al. Roaming terrain：real-time optimally adapting meshes [C]//Proceedings of IEEE Visualization’97, Phoenix, 1997:81-88.

[4]Lindstrom P, Pascucci V. Visualization of large terrains made easy [C]//Proceedings of IEEE Visualization’ 2001, san Diego, 2001: 363-370.

[5]趙友兵, 石教英, 周 驥, 等. 一種大規模地形的快速漫游算法[J].計算機輔助設計與圖形學學報, 2002,14(7): 624-628.

[6]陳少強, 朱鐵穩, 李 琦, 等. 大規模多分辨率地形模型簡化生成方法[J]. 計算機輔助設計與圖形學學報, 2005, (2): 273-278.

[7]王林旭, 李思昆, 潘曉輝. 動態地形的實時可視化[J].計算機學報, 2003, (11): 1524-1531.

[8]He Yefei, Cremer J, Papelis Y. Real-time extendibleresolution display of on-line dynamic terrain [C]//Proceedings of Graphies Interface, Calgary, Alberta.2002: 27-29.

[9]Chen Guojun, Zhang Jing. Dynamic terrain LOD with region pres ervation in 3D game engine [C]//Proceedings of the First Inte rnational Conference on E- Learning and Games, LNCS 3942, 2006: 711-715.

[10]R?ttger S, Heidrich W, Slusallek P, et al. Real-time generation of continuous lebels of detail for height fields [C]//Proceedings of the 6th International Conference in Central Europe on Computer Graphics and Visualization, 1998: 313-322.

[11]陳國軍, 崔保磊, 陳慶剛. 生成地形細節層次的粗糙度誤差判據[J]. 中國石油大學學報, 2009, (10):168-172.

[12]DISCOE Ben Elevation file repository [EB/OL].http://www.vterrain.org/BT/index.html 2007-09-11.