蛇形機器人的運動分析以及步態研究

譚啟明，何振勇，陳然

（華南理工大學廣東廣州510640）

蛇的生存環境是非常多樣化的：森林、沙漠、山地、石堆、草叢、沼澤甚至湖泊。它獨特的蜿蜒爬行方式使其在各種生態條件下都隨遇而安、運動迅速自如。適合在水下地下管道，凹凸不平的表面，墻壁之間的狹小裂縫，橋梁纜索等特殊環境下作業、具有廣泛的應用前景。文中提出了一種7關節6連桿的蠕動仿生蛇形機器人，其為行波傳遞運動方式，下面我將對這種機器人進行研究。

1 蛇形機器人的模型結構設計與步態研究

每個關節長度為：a，質量為：m，初步模擬有7個關節。電機減速器安裝在其軸線上，桿件的重量相當于關節來說可以忽略不計，因此轉軸中心作為桿件的質心，其在表面上蠕動進行時，它的簡化模型如圖1中的蛇形蠕動前行[1]。（圖2只給出了3節的運動分析）首先研究的是3動桿的運動步態，做模擬的運動圖解如圖1。

首先點P0沿著X軸前進，其他點Pi（i≥2）固定不動；于此同時，桿件P0P1與X軸之間的夾角α從0°到達給定的角度α0。

在初始階段，P0P1和P1P2運動，它們與X軸之間形成等腰三角形，在該階段結束時，三角形的底腳為（圖1中的階段c），除了P1其他點均位于X軸上。

下一階段，P0P1、P1P2和P2P3為動桿，點P0和Pi（i≥3）均保持不動，夾角α從α0變為0°，與此同時P2P3與X軸的夾角β從0°到達給定的角度α0（圖1中的階段d）；當這一階段結束時，系統處于狀態e；P1P2、P2P3與X軸之間成等腰三角形，除了P2外，其他點均位于X軸上。

重復以上的過程，將會發現當一個階段完成后，除了三角形的頂點外，其他的點均位于X軸上。頂點和三角形將會逐漸向右移動；最后點P5將會成為三角形的頂點（如圖1中的階段f），夾角α從α0變為0°，整個系統恢復為直線狀態g（如圖1中的階段g）。在這一個運動周期，整個系統沿X軸的位移L等于點P0從α0狀態a到狀態b的位移。因此有：L=2a（1-cosα0）。

其中，a為桿長。

下面我們進行系統的步態分析，為以后的仿真測試做準備，我們把系統桿件的數量設為可擴展的N，進行一個普遍的多桿蛇形機器人的步態分析[2]。

1.1 蛇形機器人的步態與位移分析

從圖2可知，在波形傳遞階段，動點為Pi和Pi+1（1≤i≤N-1），其他點靜止不動，則我們可以將Pi-1Pi、PiPi+1、Pi+1Pi+2簡化為如圖2的連桿機構，Pi+1和Pi+2之間的距離d是固定的，d=a+cosα0，那么波峰過渡階段可劃分為如圖2所示的4個階段，初始位置為圖1中的c階段結束位置為圖1中的過程e。

圖1 蛇形機器人三動桿的步態分析Fig.1 Gait analysis of snake-like robot three moving rod

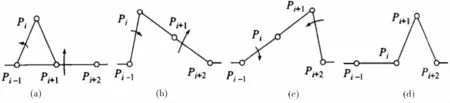
圖2 三桿件的運動的4個狀態Fig.2 Four state of the three rod movement

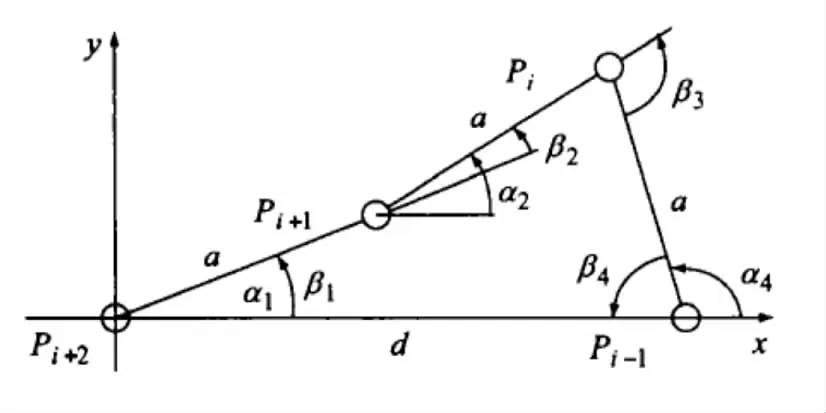
圖3 3桿件的矢量四邊形Fig.3 Three member of the vector quadrilateral

由圖3所示的封閉矢量四邊形Pi-1PiPi+1Pi+2得：

其在X、Y軸上分解得：

消去α4后得：

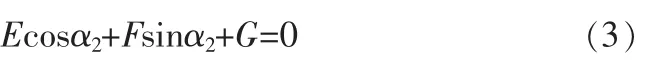
解出：

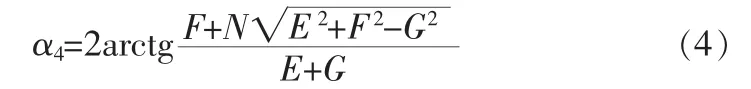
式中N為符號系數，ΔPi+1Pi-1Pi三頂點的順序為逆時針方向，N=-1；順時針方向N=1；這是按照右手直角坐標系制定的，如為左手坐標系，則判別N符號的規則上相反。

又由公式（2）可以解得：

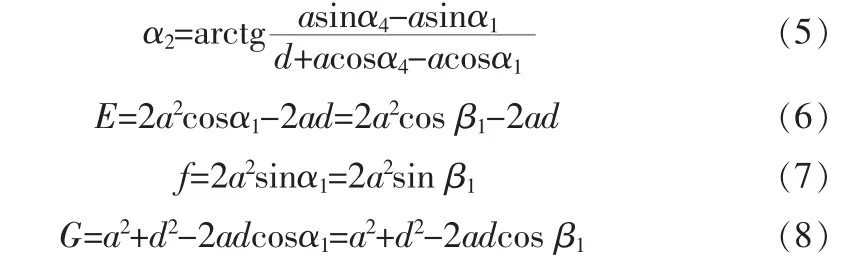
通過式（6）、式（7）和式（8）可以將連桿的各個角度均由β1表示，對研究其角度關系提供基礎。

1.2 蛇形機器人各連桿間的相對角位移

由圖3設各已知Pi+1Pi+2相對Pi+2Pi+3的轉角β1，則各連桿的相對轉角都可用β1來表示，由圖3的幾何關系可以推導出以下的角速度關系式：

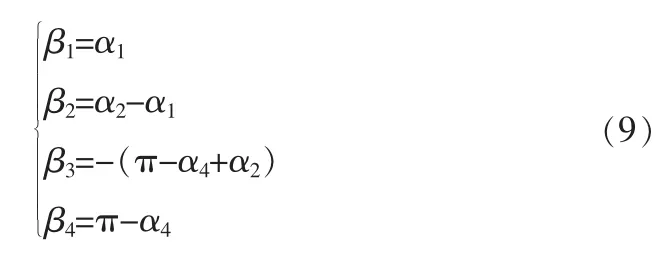
由式9可以得出，各個轉角關系都可以用β1表示，則按照角度設計蛇形機器人的旋轉驅動可以設置轉角β1為變量的函數[3]。

1.3 蛇形機器人設計

有前文推導可以設計蛇形機器人的旋轉函數，只涉及轉角β2與β1，其他連桿由于其為剛性連桿，并且通過旋轉鉸鏈相連，則可以連帶轉動，整個蛇形機器人前進一步的具體設計分為3大部分[4]：

1）過程一：

桿0-1沿著右端點2處旋轉副做向X軸正方向的順時針旋轉，點1不固定在地面上，其他點均施加大的摩擦力固定在地面上，旋轉到桿1-2與X軸負方向成60°時停止轉動，運動的過程中點0設置為高副滑動，如圖4所示。

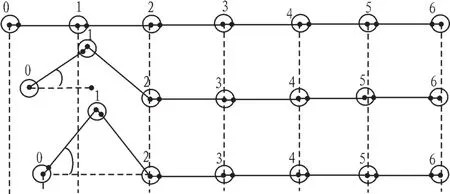
圖4 過程一：步態設計圖Fig.4 Process 1:Gait design

在此過程中，只設計端點1處的旋轉角度的函數，通過此函數，可以使蛇形機器人尾部抬起一定角度。由于研究機器人的步態過程，對其加速度和速度先進行忽略處理，只研究端點1的轉角度數與時間的函數，建立緩慢變化的階躍函數，其函數表達式可以表示為：

y為端點1角度變化（度），x為時間（秒）：

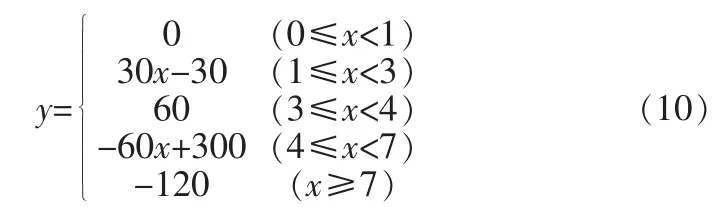
在此還要說明的是，在4 s之前，端點2不受函數控制，為自由鉸鏈，在4 s之后執行式12的函數，轉動端點2。

之后的運動，為循環每個端點的階躍函數，定義域一直向后平移，直至蛇形機器人的波形向最后一節移動。

2）過程二：

到最后連桿4-5沿著左邊端點4向X軸正方向做順時針旋轉，最后端點6做與地面接觸的高副運動，如圖5所示。

圖5 過程二：步態設計圖Fig.5 Process 1:Gait design

在過程二中，可以只設計端點2處的轉角函數，通過轉動端點2處的角度，其他剛性桿隨之運動，在此過程中端點1處由過程一結束時的銳角變為鈍角（轉過了180°），所以在端點1處的轉角函數處加上式（11）的后兩式，此處端點2的轉角函數與端點1的轉角函數形狀相同，只是定義域向右平移了轉角一運動的一半過程。

y為端點2角度變化（度），x為時間（秒）：

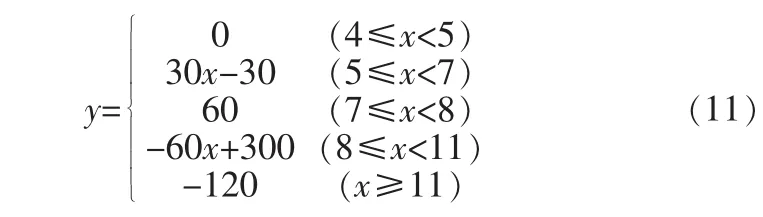
在此還要說明的是，在4 s之前，端點2不受函數控制，為自由鉸鏈，在4 s之后執行式（12）的函數，轉動端點2。

之后的運動，為循環每個端點的階躍函數，定義域一直向后平移，直至蛇形機器人的波形向最后一節移動[5]。

3）過程三：

到最后連桿4-5沿著左邊端點4向X軸正方向做順時針旋轉，最后端點6做與地面接觸的高副運動，如圖6所示。

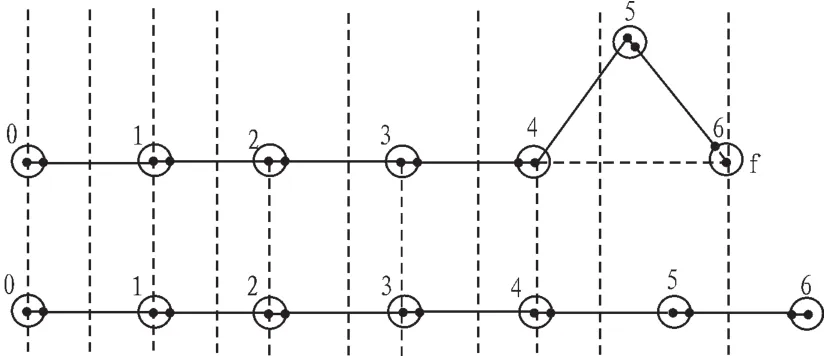
圖6 過程三：步態設計圖Fig.6 Process 1:Gait design

當波形運動到最后一個端點5時，端點5的運動開始時間為20 s，則此端點的轉動角度函數。

y為端點5角度變化（度），x為時間（秒）：

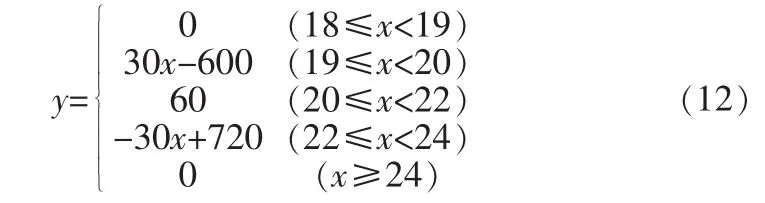
最后蛇形機器人的端點全部位于x軸上，蛇形機器人前進一個步態[6]。

2 結束語

文中主要研究了蛇形機器人的一般模型，在這些模型的基礎上，提出了一種行波式的運動模型，對模型的結構建立和步態進行分析及其數學計算，為之后的仿真模型建立了數學基礎。

[1] Bayraktaroglu Z Y.Snake-like locomotion:Experimentations withabiologically inspiredwheel-lesssnake robot[J].Mechanism and Machine Theory，2009，44:591-602.

[2] Prantsch P，Mira T.Control and analysis of the gait of snake robts[C]//In IEEE International Conference OR Control Applications，1999:502-507.

[3]Chernousko F L.Snake-like locomotions of multilink systems，in Virtual Nonlinear Multibody Systems[J].NATO Science Series，2003：452-458.

[4] Tanev I，Ray T，Buller A.Automated evolutionary design，robustness，and adaptation of sidewinding locomotion of a simulated snake-like robot[C]//IEEE Transactions on Robotics，2005，21（4）:632-645.

[5] 徐亮，王興松.蠕動機器蛇的仿生設計和運動學分析[J].機電工程技術，2007，36（12）:79-83.XU Liang，WANG Xing-song.The peristaltic snake robot bionic design and kinematic analysis of[J].Mechanical&electrical engineering technology，2007，36（12）:79-83.

[6] 孫洪.攀爬蛇形機器人的研究[D].上海：上海交通大學，2007.